| Citation: |
Yipeng Jiao, Kangliang Wei, Taihuan Wang, Gang Du, Xiaoyan Liu. Comparison of band-to-band tunneling models in Si and Si-Ge junctions[J]. Journal of Semiconductors, 2013, 34(9): 092002. doi: 10.1088/1674-4926/34/9/092002
****
Y P Jiao, K L Wei, T H Wang, G Du, X Y Liu. Comparison of band-to-band tunneling models in Si and Si-Ge junctions[J]. J. Semicond., 2013, 34(9): 092002. doi: 10.1088/1674-4926/34/9/092002.
|
Comparison of band-to-band tunneling models in Si and Si-Ge junctions
DOI: 10.1088/1674-4926/34/9/092002
More Information
-
Abstract
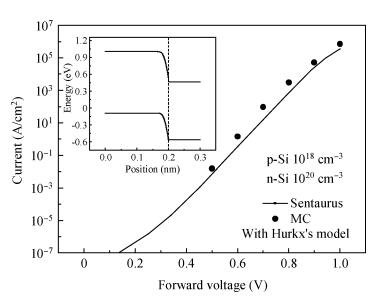
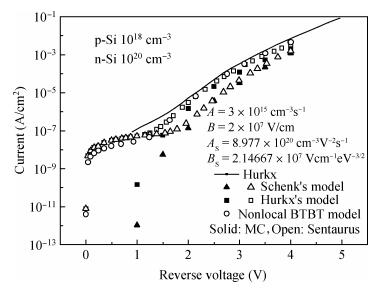
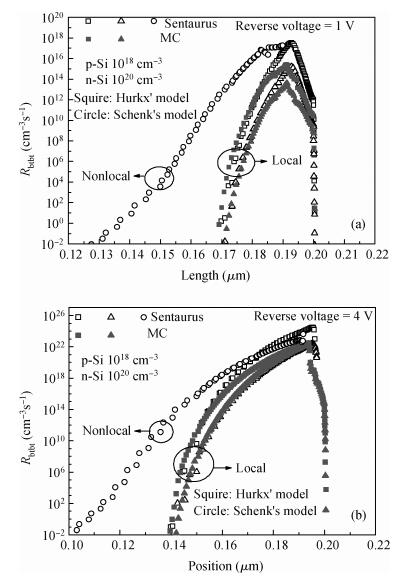
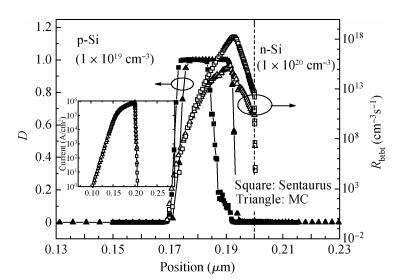
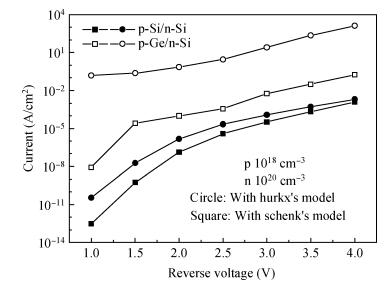
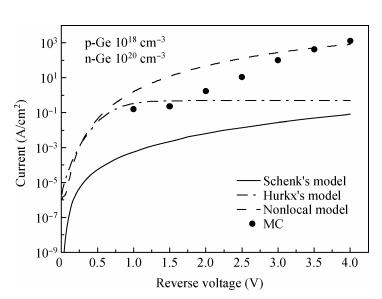
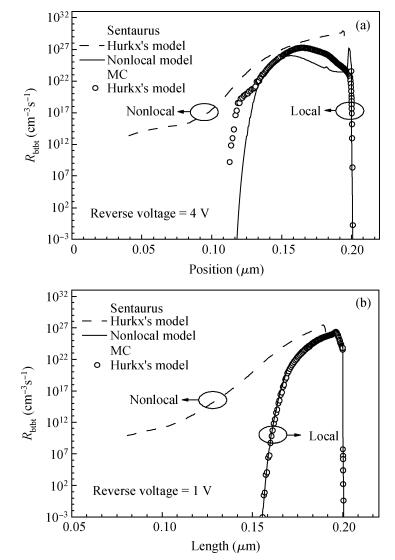
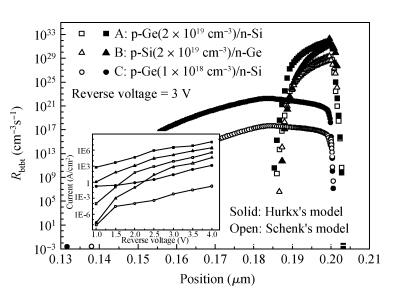
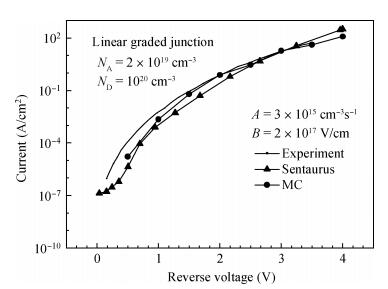
We compared several different band-to-band tunneling (BTBT) models with both Sentaurus and the two-dimensional full-band Monte Carlo simulator in Si homo-junctions and Si-Ge hetero-junctions. It was shown that in Si homo-junctions, different models could achieve similar results. However, in the Si-Ge hetero-junctions, there were significant differences among these models at high reverse biases (over 2 V). Compared to the nonlocal model, the local models in Sentaurus underrated the BTBT rate distinctly, and the Monte Carlo method was shown to give a better approximation. Additionally, it was found that in the Si region near the interface of the Si-Ge hetero-junctions, the direct tunneling rates increased largely due to the interaction of the band structures of Si and Ge. -
References
[1] Vandenberghe W, Sorée B, Magnus W, et al. Generalized phonon-assisted Zener tunneling in indirect semiconductors with non-uniform electric fields:a rigorous approach. J Appl Phys, 2011, 109(12):124503 doi: 10.1063/1.3595672[2] Kim S H, Kam H, Hu C, et al. Germanium-source tunnel field effect transistors with record high ION/IOFF. IEEE Symposium on VLSI Technology (VLSIT), 2009:178 http://ieeexplore.ieee.org/document/5200679/[3] Luisier M, Klimeck G. Performance comparisons of tunneling field effect transistors made of InSb, Carbon, and GaSb-InAs broken gap hetero-structures. IEEE International Electron Devices Meeting (IEDM), 2009:1 doi: 10.1007%2Fs00339-016-0151-3.pdf[4] Avci U E, Rios R, Kuhn K, et al. Comparison of performance, switching energy and process variations for the TFET and MOSFET in logic. IEEE Symposium on VLSI Technology (VLSIT), 2011:124 doi: 10.1007/978-3-319-31653-6_4/fulltext.html[5] Krishnamohan T, Kim D, Raghunathan S, et al. Double-gate strained-Ge hetero-structure tunneling FET (TFET) with record high drive currents and <<ll 60 mV/dec sub threshold slope. IEEE International Electron Devices Meeting (IEDM), 2008:1[6] Chynoweth A G, Feldmann W L, Lee C A, et al. Internal field emission at narrow silicon and germanium pn junctions. Phys Rev, 1960, 118(2):425 doi: 10.1103/PhysRev.118.425[7] Ionescu A M, Riel H. Tunnel field-effect transistors as energy-efficient electronic switches. Nature, 2011, 479(7373):329 doi: 10.1038/nature10679[8] Wei K L, Zeng L, Wang J C, et al. Simulation of band-to-band tunneling in Si/Ge and Si/Si1-xGex hetero-junctions by using Monte Carlo method. IEEE International Conference on Solid-State and Integrated Circuit Technology (ICSICT), 2012:1[9] Xia Z L, Du G, Song Y C, et al. Monte Carlo simulation of band-to-band tunneling in silicon devices. Jpn J Appl Phys, 2007, 46:2023 doi: 10.1143/JJAP.46.2023[10] Hurkx G A M, Klaassen D B M, Knuvers M P G. A new recombination model for device simulation including tunneling. IEEE Trans Electron Devices, 1992, 39(2):331 doi: 10.1109/16.121690[11] Liou J J. Modeling the tunneling current in reverse-biased p/n junctions. Solid-State Electron, 1990, 33(7):971 doi: 10.1016/0038-1101(90)90081-O[12] Schenk A. Rigorous theory and simplified model of the band-to-band tunneling in silicon. Solid-State Electron, 1993, 36(1):19 doi: 10.1016/0038-1101(93)90065-X[13] Fischetti M V, O'Regan T P, Narayanan S, et al. Theoretical study of some physical aspects of electronic transport in nMOSFETs at the 10-nm gate-length. IEEE Trans Electron Devices, 2007, 54(9):2116 doi: 10.1109/TED.2007.902722[14] Kao K H, Verhulst A S, Vandenberghe W G, et al. Direct and indirect band-to-band tunneling in germanium-based TFETs. IEEE Trans Electron Devices, 2012, 59(2):292 doi: 10.1109/TED.2011.2175228[15] Kane E O. Theory of tunneling. J Appl Phys, 1961, 32(1):83 doi: 10.1063/1.1735965[16] Sentaurus Device, Synopsys, Version D-2010. 03: 362[17] Wernersson L E, Kabeer S, Zela V, et al. SiGe Esaki tunnel diodes fabricated by UHV-CVD growth and proximity rapid thermal diffusion. Electron Lett, 2004, 40(1):83 doi: 10.1049/el:20040048[18] Wei K L, Liu X Y, Du G, et al. Simulation of carrier transport in hetero-structures using the 2D self-consistent full-band ensemble Monte Carlo method. Journal of Semiconductors, 2010, 31(8):084004 doi: 10.1088/1674-4926/31/8/084004[19] Du G, Liu X Y, Xia Z L, et al. Monte Carlo simulation of p-and n-channel GOI MOSFETs by solving the quantum Boltzmann equation. IEEE Trans Electron Devices, 2005, 52(10):2258 doi: 10.1109/TED.2005.856806 -
Proportional views





 DownLoad:
DownLoad: