| Citation: |
Guodong Ren, Shifang Zhao, Zhongshen Pu, Zhiqiang Wei. Compact trimming design of a high-precision reference[J]. Journal of Semiconductors, 2014, 35(4): 045008. doi: 10.1088/1674-4926/35/4/045008
****
G D Ren, S F Zhao, Z S Pu, Z Q Wei. Compact trimming design of a high-precision reference[J]. J. Semicond., 2014, 35(4): 045008. doi: 10.1088/1674-4926/35/4/045008.
|
Compact trimming design of a high-precision reference
DOI: 10.1088/1674-4926/35/4/045008
More Information
-
Abstract
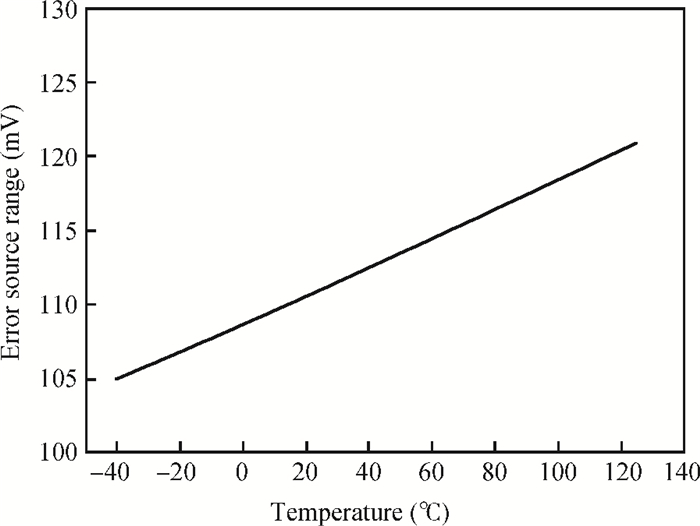
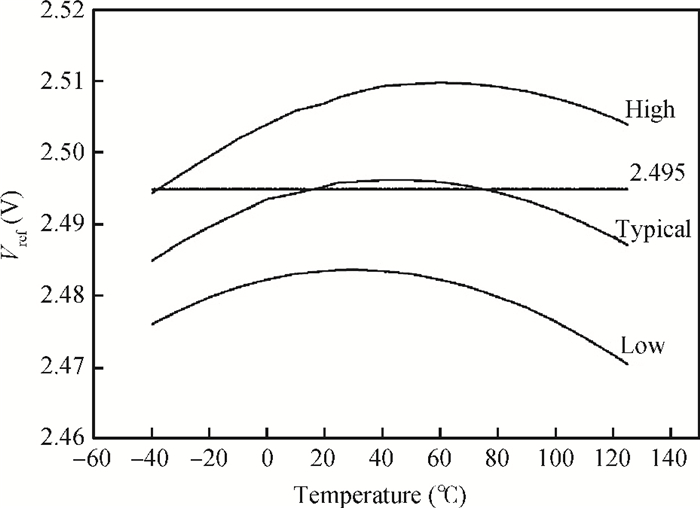
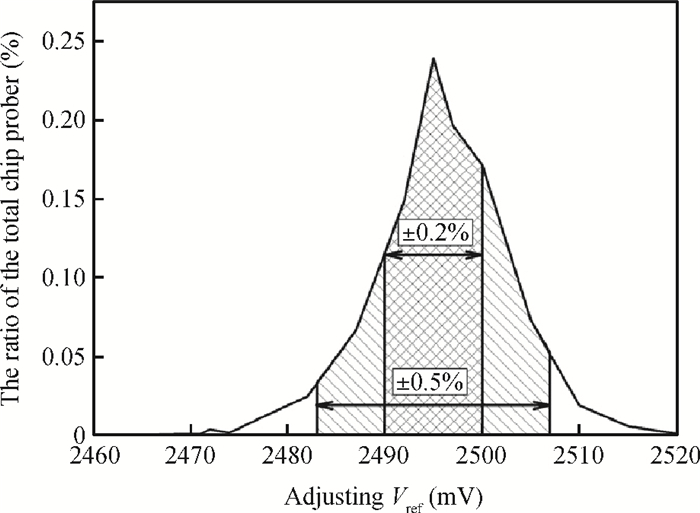
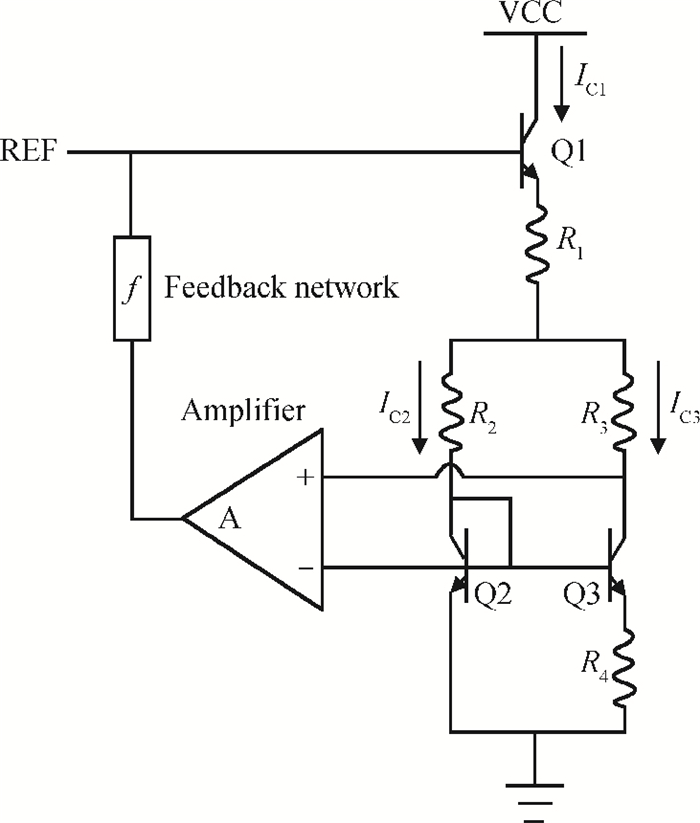
To design a high-precision reference, the various error sources have been analyzed and compensated with a compact 111 mV resistor-trim scheme and the upper and lower extremes of the reference precision are also temperature-compensated. At room temperature, the yield of ±0.5% precision is 96% and ±0.2% is 78%.-
Keywords:
- high-precision,
- error sources,
- trim,
- temperature-compensated
-
References
[1] Basso C, Kadanka P. The TL431 in switch-mode power supplies loops:part Ⅰ. Electronic Design and Application World-Nikkei Electronics China, 2009, (3):99[2] Meijer G C, Wang G, Fruett F. Temperature sensors and voltage references implemented in COMS technology. IEEE J Sensors, 2001, 1(3):225 doi: 10.1109/JSEN.2001.954835[3] Palumbo G. Voltage references from diodes to precision high-order bandgap circuits. IEEE Circuits and Devices Magazine, 2002, 18(5):45 doi: 10.1109/MCD.2002.1035357[4] Song B S, Gray P R. A precision curvature-compensated CMOS bandgap reference. IEEE J Solid-State Circuits, 1983, 18(6):634 doi: 10.1109/JSSC.1983.1052013[5] Meijer G M, Fonderie C. A curvature-corrected low-voltage bandgap reference. IEEE J Solid-State Circuits, 1993, 28(6):667 doi: 10.1109/4.217981[6] Sheng Jinggang, Chen Zhiliang, Shi Bingxue. A CMOS bandgap reference with 1 V supply. Chinese Journal of Semiconductors, 2005, 26(4):826 https://www.researchgate.net/publication/293255783_CMOS_bandgap_reference_with_1V_supply[7] Xu Yong, Wang Zhigong, Guan Yu. Improved design of a bandgap voltage reference with high accuracy. Chinese Journal of Semiconductors, 2006, 27(12):2209 https://www.researchgate.net/publication/291296647_Improved_design_of_a_bandgap_voltage_reference_with_high_accuracy[8] Gupta V, Rincón-Mora G A. Predicting and designing for the impact of process variations and mismatch on the trim range and yield of bandgap reference. Quality of Electronic Design, 2005:503 http://dl.acm.org/citation.cfm?id=1049711&CFID=426924195&CFTOKEN=68355621[9] Hastings A. The art of analog layout. Beijing:Tsinghua University Press, 2004[10] Anderson B L, Anderson R L. Fundamentals of semiconductor devices. Beijing:Tsinghua University Press, 2006[11] Gupta V, Rincón-Mora G A. Predicting the effects of error sources in bandgap reference circuits and evaluating their design implications. Circuits and Systems, 2002, 3:575 http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1187105[12] TLV431 Datasheet[c]. 2000-2005 Texas Instruments Incorporated -
Proportional views





 DownLoad:
DownLoad: