| Citation: |
M. Hema Lata Rao, N. V. L. Narasimha Murty. An improved analytical model of 4H-SiC MESFET incorporating bulk and interface trapping effects[J]. Journal of Semiconductors, 2015, 36(1): 014004. doi: 10.1088/1674-4926/36/1/014004
****
M. H. L. Rao, N. V. L. N. Murty. An improved analytical model of 4H-SiC MESFET incorporating bulk and interface trapping effects[J]. J. Semicond., 2015, 36(1): 014004. doi: 10.1088/1674-4926/36/1/014004.
|
An improved analytical model of 4H-SiC MESFET incorporating bulk and interface trapping effects
DOI: 10.1088/1674-4926/36/1/014004
More Information
-
Abstract
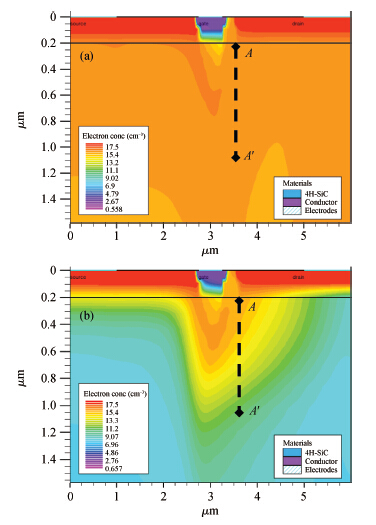
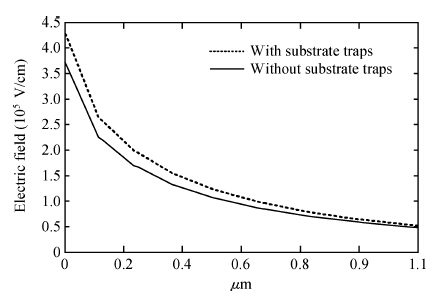
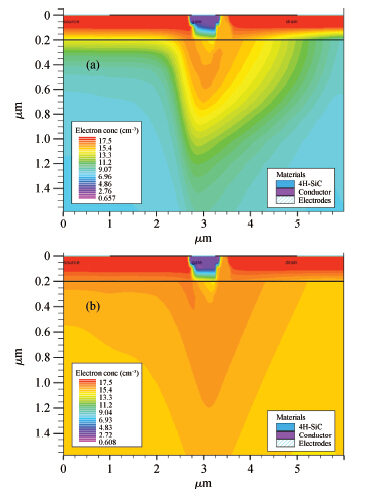
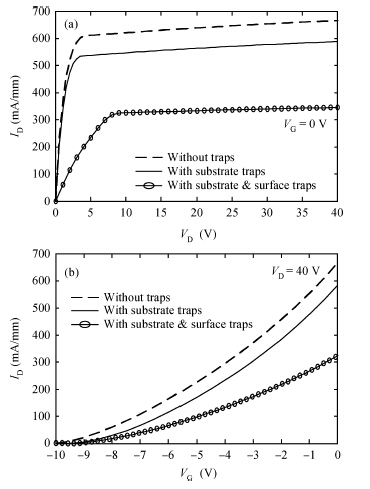
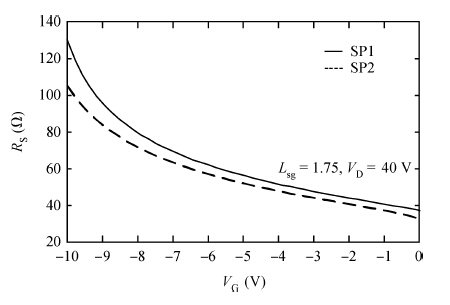
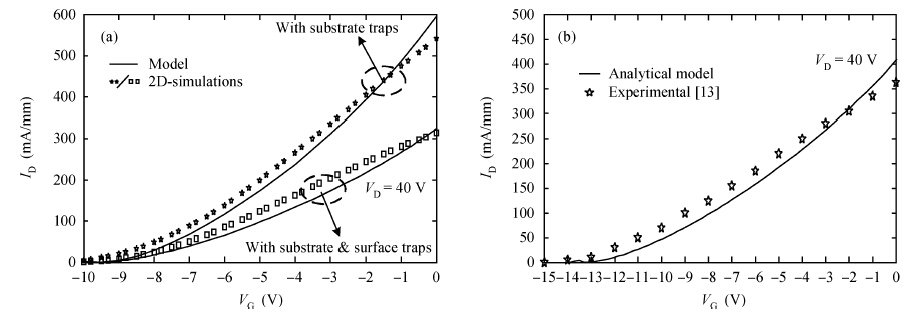
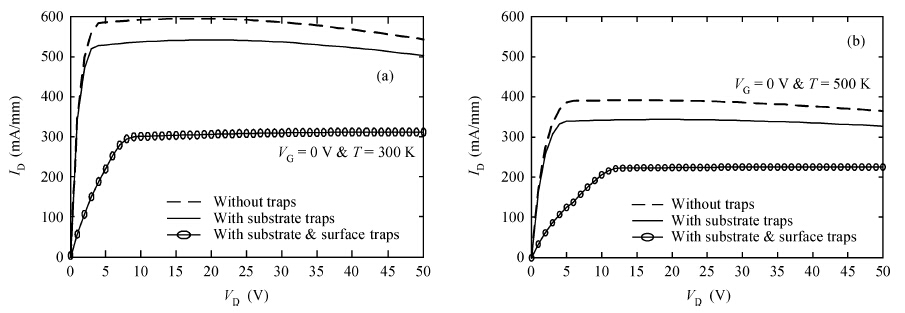
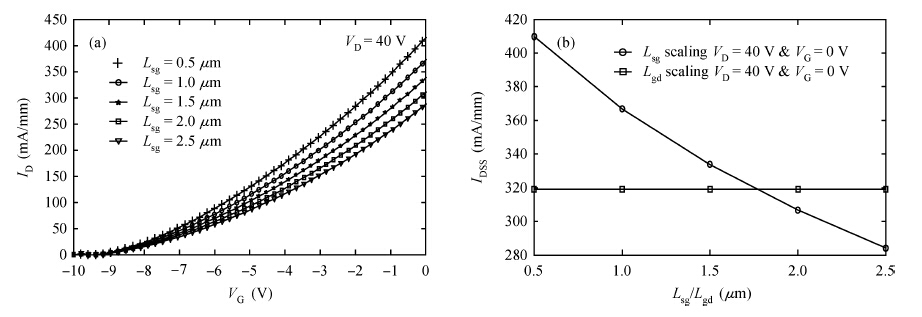
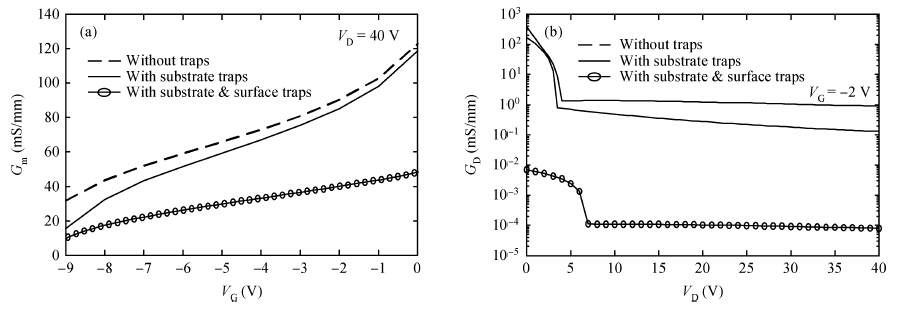
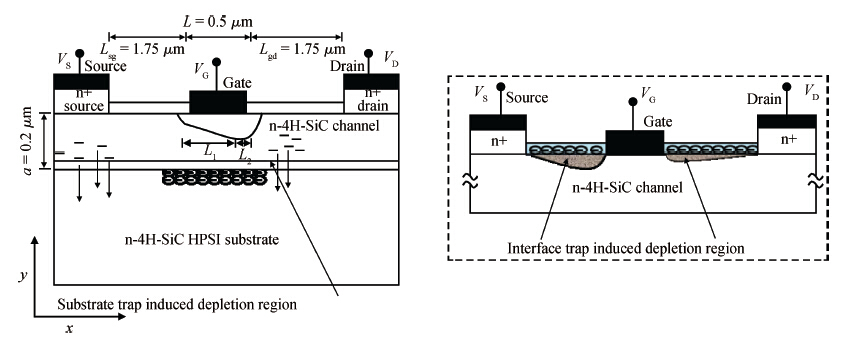
An improved analytical model for the current-voltage (I-V) characteristics of the 4H-SiC metal semiconductor field effect transistor (MESFET) on a high purity semi-insulating (HPSI) substrate with trapping and thermal effects is presented. The 4H-SiC MESFET structure includes a stack of HPSI substrates and a uniformly doped channel layer. The trapping effects include both the effect of multiple deep-level traps in the substrate and surface traps between the gate to source/drain. The self-heating effects are also incorporated to obtain the accurate and realistic nature of the analytical model. The importance of the proposed model is emphasised through the inclusion of the recent and exact nature of the traps in the 4H-SiC HPSI substrate responsible for substrate compensation. The analytical model is used to exhibit DC I-V characteristics of the device with and without trapping and thermal effects. From the results, the current degradation is observed due to the surface and substrate trapping effects and the negative conductance introduced by the self-heating effect at a high drain voltage. The calculated results are compared with reported experimental and two-dimensional simulations (Silvaco®-TCAD). The proposed model also illustrates the effectiveness of the gate-source distance scaling effect compared to the gate-drain scaling effect in optimizing 4H-SiC MESFET performance. Results demonstrate that the proposed I-V model of 4H-SiC MESFET is suitable for realizing SiC based monolithic circuits (MMICs) on HPSI substrates.-
Keywords:
- SiC MESFET,
- HPSI substrate,
- deep-level traps,
- MMICs
-
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] -
Proportional views





 DownLoad:
DownLoad: