| Citation: |
Xiyan Jiang, Jin Wang, Chen Gao, Ji Xu, Hongdan Wan. All-optical NRZ wavelength conversion using a Sagnac loop with optimized SOA characteristics[J]. Journal of Semiconductors, 2015, 36(1): 014013. doi: 10.1088/1674-4926/36/1/014013
****
X Y Jiang, J Wang, C Gao, J Xu, H D Wan. All-optical NRZ wavelength conversion using a Sagnac loop with optimized SOA characteristics[J]. J. Semicond., 2015, 36(1): 014013. doi: 10.1088/1674-4926/36/1/014013.
|
All-optical NRZ wavelength conversion using a Sagnac loop with optimized SOA characteristics
DOI: 10.1088/1674-4926/36/1/014013
More Information
-
Abstract
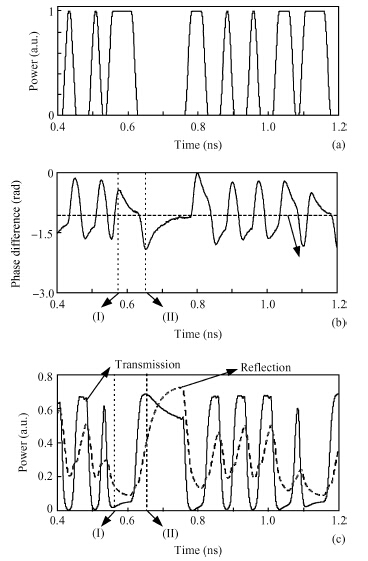
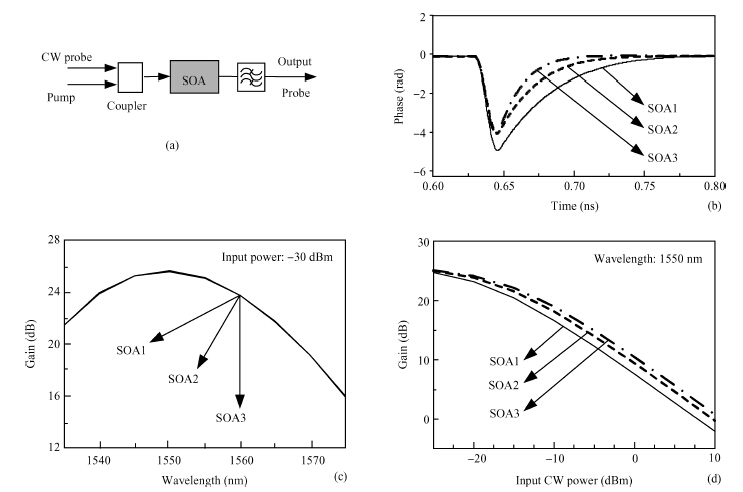
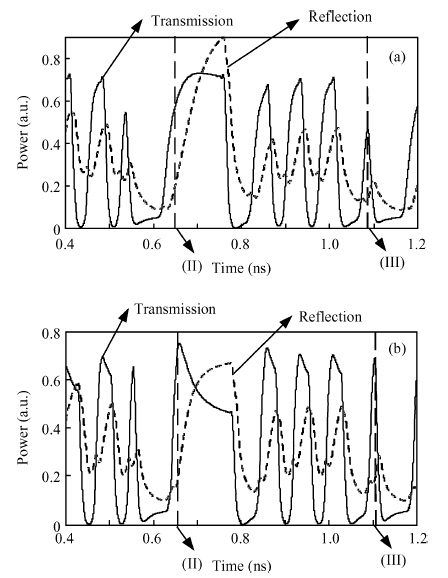
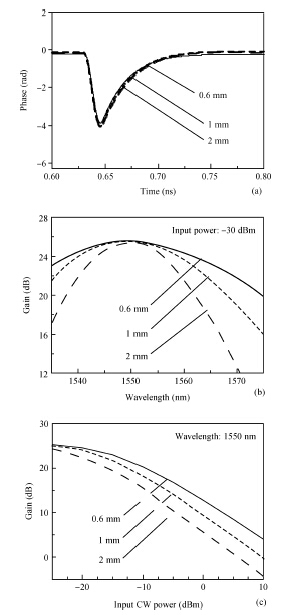
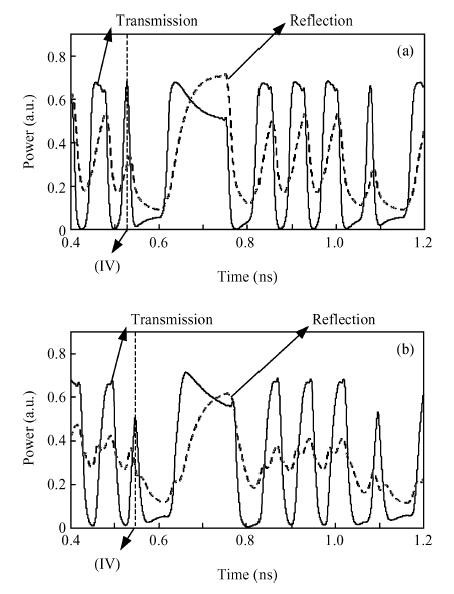
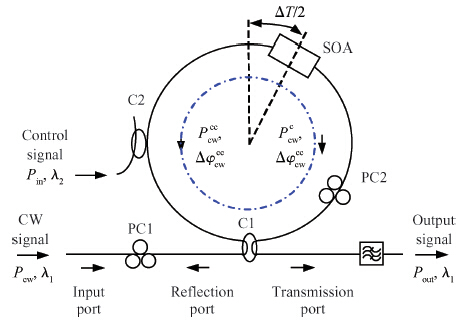
We investigated the all-optical wavelength conversion technique for non-return-to-zero (NRZ) signals based on a Sagnac loop interferometer using an SOA. For the wavelength conversion of the NRZ signal at and above 40 Gbit/s, we used an in-house numerical SOA model to analyze the influence of the SOA carrier characteristics and the SOA length on the performance of the Sagnac loop. We found that the SOA carrier recovery time should be between 2 and 3 times of one bit duration in order to get optimum NRZ wavelength conversion. In addition to the carrier recovery time requirement, SOAs with a shorter physical length are preferred to be used in the Sagnac interferometer. -
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] -
Proportional views





 DownLoad:
DownLoad: