| Citation: |
Chong Lu, Hongzhou Tan, Zhikui Duan, Yi Ding. A high-precision synchronization circuit for clock distribution[J]. Journal of Semiconductors, 2015, 36(10): 105004. doi: 10.1088/1674-4926/36/10/105004
****
C Lu, H Z Tan, Z K Duan, Y Ding. A high-precision synchronization circuit for clock distribution[J]. J. Semicond., 2015, 36(10): 105004. doi: 10.1088/1674-4926/36/10/105004.
|
-
Abstract
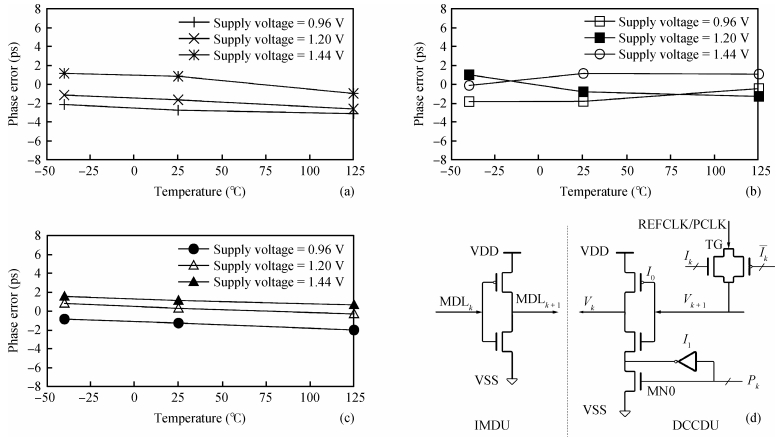
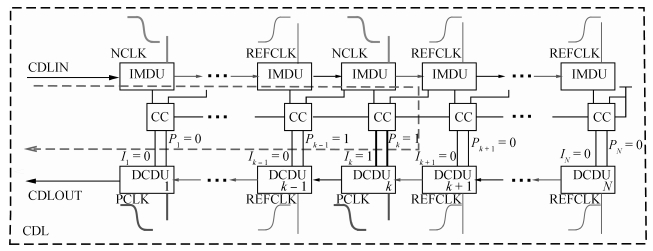
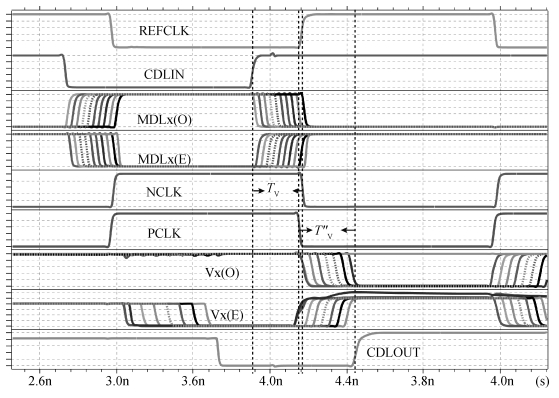
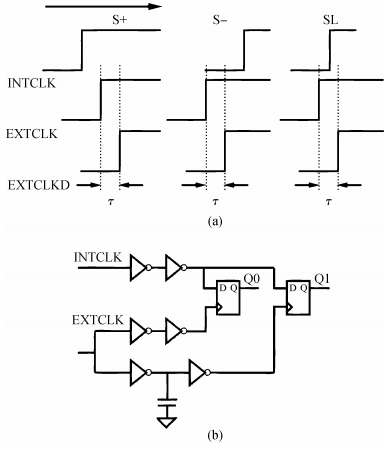
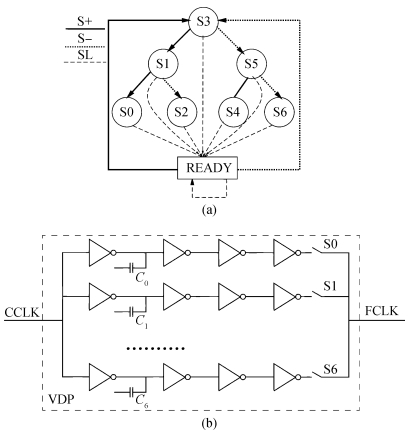
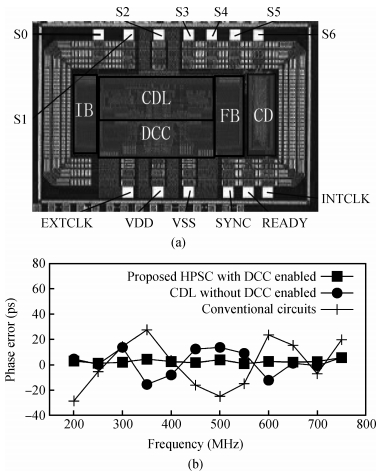
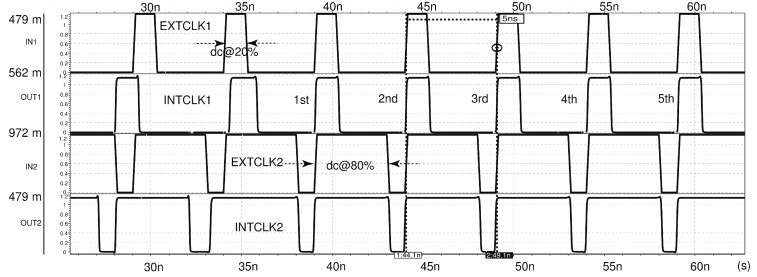
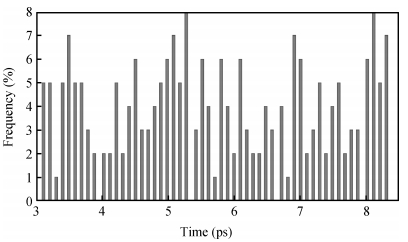
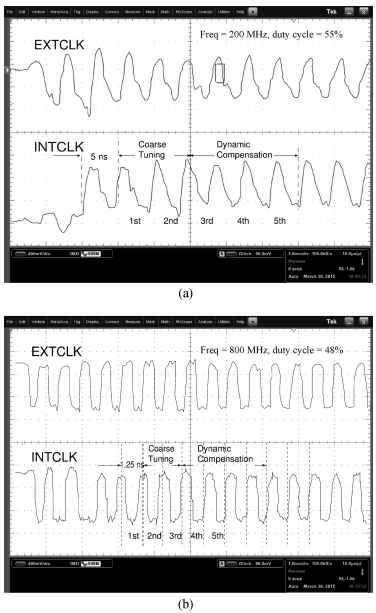
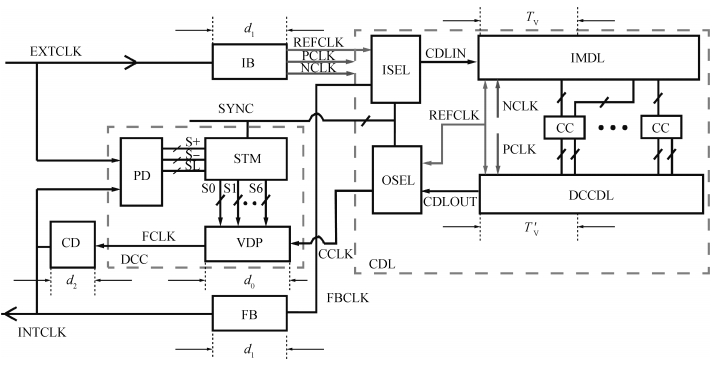
In this paper, a novel structure of a high-precision synchronization circuit, HPSC, using interleaved delay units and a dynamic compensation circuit is proposed.HPSCs are designed for synchronization of clock distribution networks in large-scale integrated circuits, where high-quality clocks are required.The application of a hybrid structure of a coarse delay line and dynamic compensation circuit performs roughly the alignment of the clock signal in two clock cycles, and finishes the fine tuning in the next three clock cycles with the phase error suppressed under 3.8 ps.The proposed circuit is implemented and fabricated using a SMIC 0.13 μm 1P6M process with a supply voltage at 1.2 V.The allowed operation frequency ranges from 200 to 800 MHz, and the duty cycle ranges between [20%,80%].The active area of the core circuits is 245×134 μm2, and the power consumption is 1.64 mW at 500 MHz. -
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] -
Proportional views





 DownLoad:
DownLoad: