| Citation: |
Yuanfu Zhao, Chunqing Yu, Long Fan, Suge Yue, Maoxin Chen, Shougang Du, Hongchao Zheng. A prediction technique for single-event effects on complex integrated circuits[J]. Journal of Semiconductors, 2015, 36(11): 115003. doi: 10.1088/1674-4926/36/11/115003
****
Y F Zhao, C Q Yu, L Fan, S G Yue, M X Chen, S G Du, H C Zheng. A prediction technique for single-event effects on complex integrated circuits[J]. J. Semicond., 2015, 36(11): 115003. doi: 10.1088/1674-4926/36/11/115003.
|
A prediction technique for single-event effects on complex integrated circuits
DOI: 10.1088/1674-4926/36/11/115003
More Information
-
Abstract
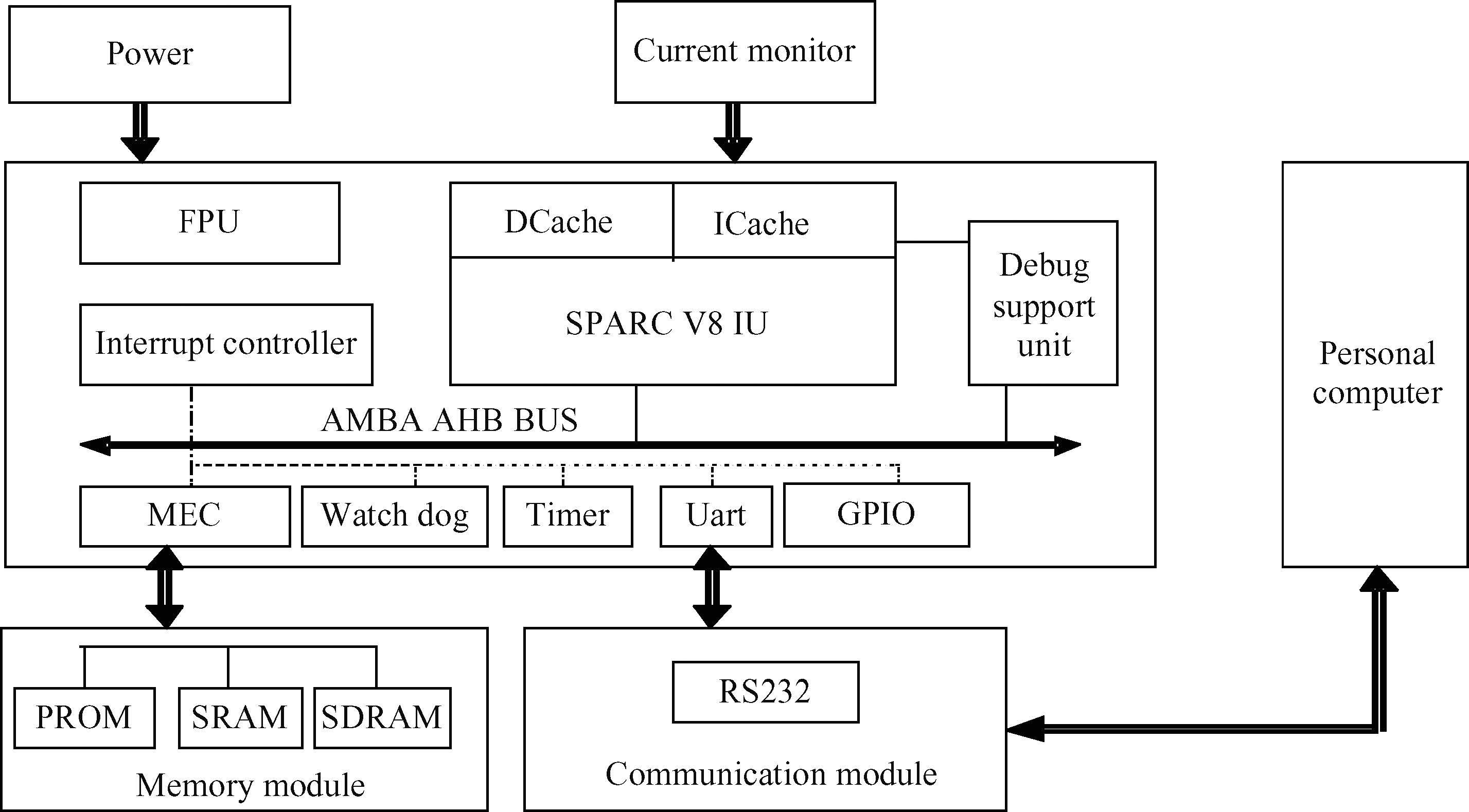
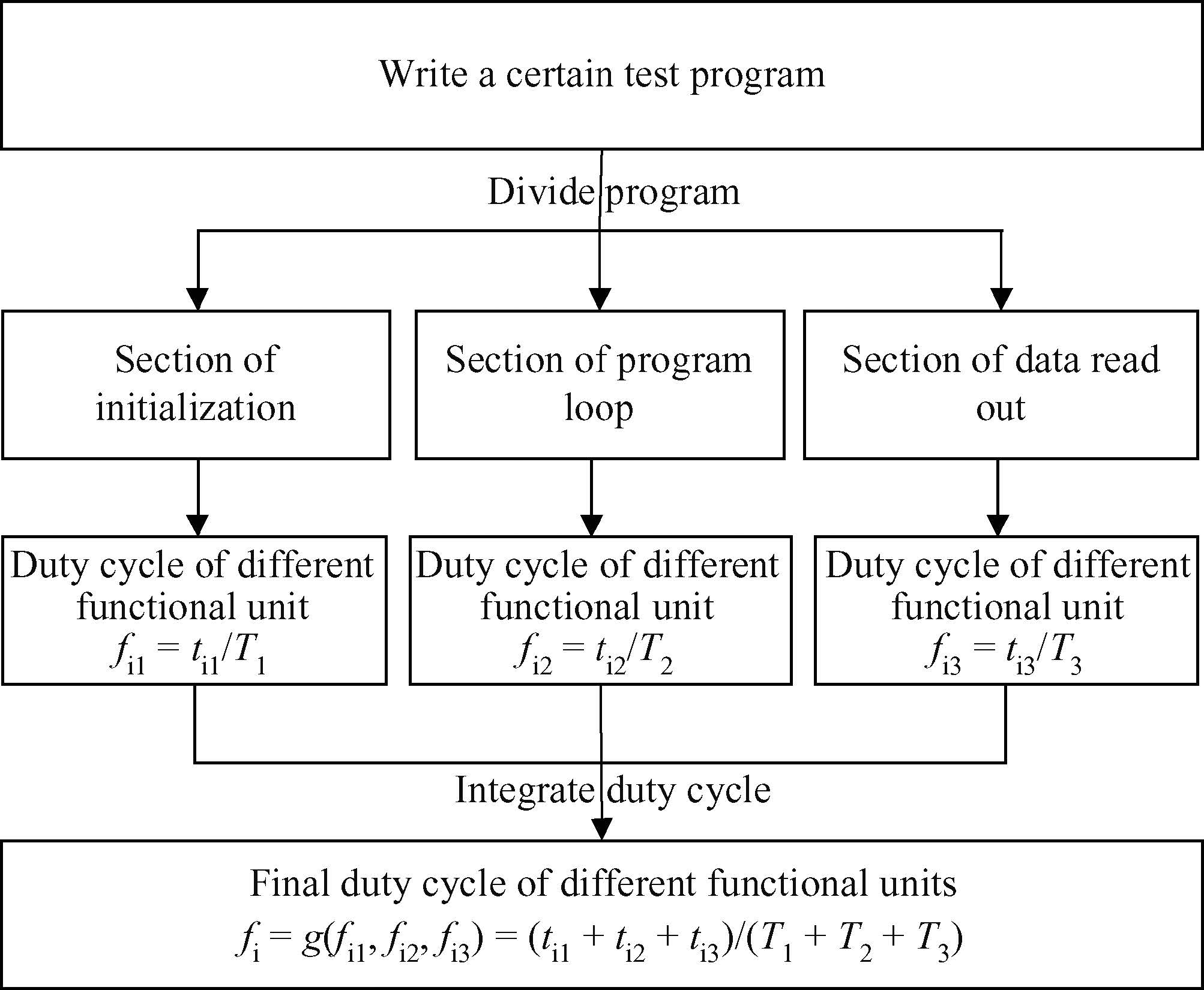
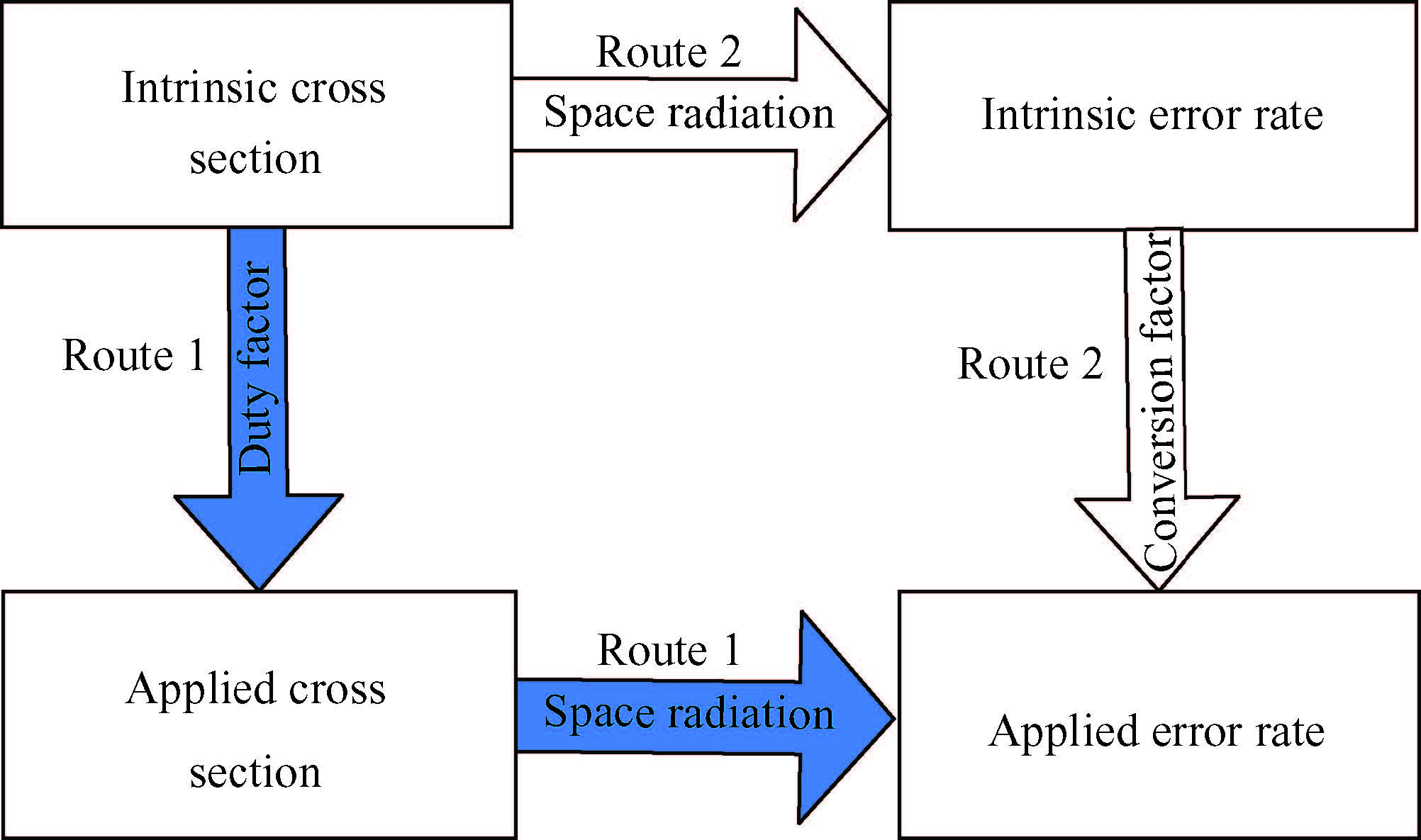
The sensitivity of complex integrated circuits to single-event effects is investigated. Sensitivity depends not only on the cross section of physical modules but also on the behavior of data patterns running on the system. A method dividing the main functional modules is proposed. The intrinsic cross section and the duty cycles of different sensitive modules are obtained during the execution of data patterns. A method for extracting the duty cycle is presented and a set of test patterns with different duty cycles are implemented experimentally. By combining the intrinsic cross section and the duty cycle of different sensitive modules, a universal method to predict SEE sensitivities of different test patterns is proposed, which is verified by experiments based on the target circuit of a microprocessor. Experimental results show that the deviation between prediction and experiment is less than 20%. -
References
[1] [2] [3] [4] [5] -
Proportional views





 DownLoad:
DownLoad: