J. Semicond. > 2015, Volume 36 > Issue 6 > 064003
|

SEMICONDUCTOR DEVICES

Analysis of charge density and Fermi level of AlInSb/InSb single-gate high electron mobility transistor

S. Theodore Chandra1, N. B. Balamurugan1, M. Bhuvaneswari2, N. Anbuselvan2 and N. Mohankumar2

+ Author Affiliations

 Corresponding author: E-amil: theodore@tce.edu

DOI: 10.1088/1674-4926/36/6/064003

PDF

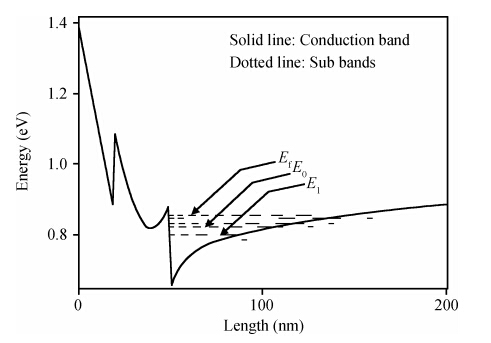
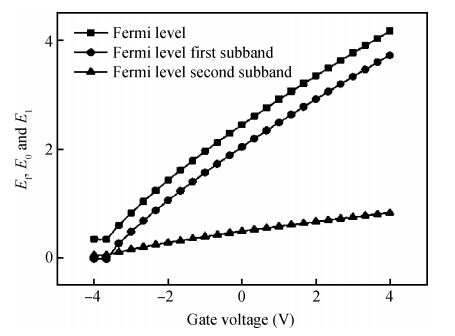
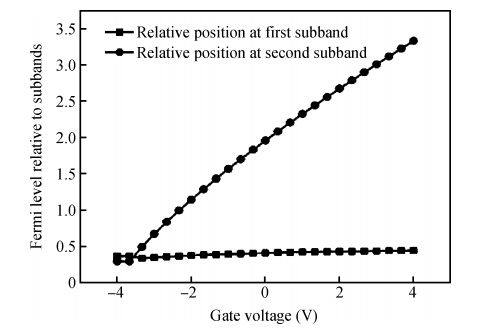
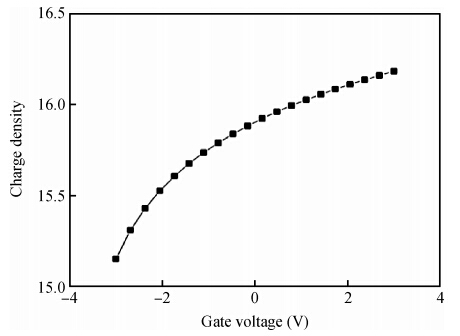
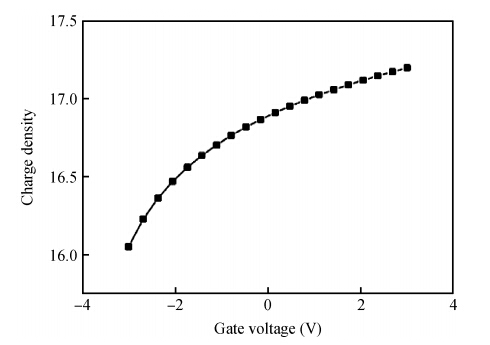
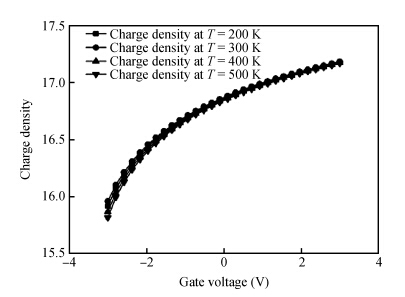
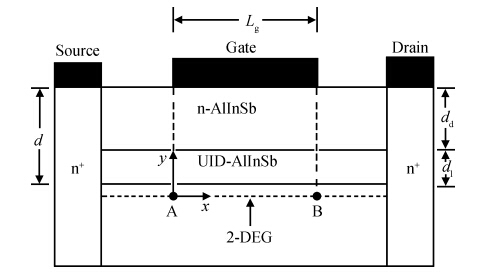
Abstract: A compact model is proposed to derive the charge density of the AlInSb/InSb HEMT devices by considering the variation of Fermi level, the first subband, the second subband and sheet carrier charge density with applied gate voltage. The proposed model considers the Fermi level dependence of charge density and vice versa. The analytical results generated by the proposed model are compared and they agree well with the experimental results. The developed model can be used to implement a physics based compact model for an InSb HEMT device in SPICE applications.

Key words: charge density, Fermi level, high electron mobility transistor, 2D analytical model



[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
Fig. 1.  Cross-sectional view of AlInSb/InSb HEMTs with gate length $L_{\rm g}$, $d_{\rm i}$ spacer layer thickness and $d_{\rm d}$ n-AlInSb layer thickness.

DownLoad: Full-Size Img PowerPoint
Fig. 2.  Conduction band structure with sub bands and Fermi level energy levels.

DownLoad: Full-Size Img PowerPoint
Fig. 3.  Numerical calculations of Ef, E0 and E1 versus gate voltage at T = 298 K.

DownLoad: Full-Size Img PowerPoint
Fig. 4.  Numerical calculations of $E_{\rm f}-E_0$ and $E_{\rm f}-E_1$ versus gate voltage at $T=$ 298 K.

DownLoad: Full-Size Img PowerPoint
Fig. 5.  Charge density for region I with thermal voltage versus gate voltage.

DownLoad: Full-Size Img PowerPoint
Fig. 6.  Charge density for region I without thermal voltage versus gate voltage.

DownLoad: Full-Size Img PowerPoint
Fig. 7.  Charge density for region II with thermal voltage versus gate voltage.

DownLoad: Full-Size Img PowerPoint
Fig. 8.  Charge density for region II without thermal voltage versus gate voltage.

DownLoad: Full-Size Img PowerPoint
Fig. 9.  Unified model for charge density versus gate voltage.

DownLoad: Full-Size Img PowerPoint
Fig. 10.  Charge density at various temperatures ($T=$ 200, 300, 400, 500 K) versus gate voltage.

DownLoad: Full-Size Img PowerPoint
DownLoad: CSV
DownLoad: CSV
DownLoad: CSV
DownLoad: CSV

Table 1.   List of symbols and parameters used.

DownLoad: CSV
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]

    • Search

    Advanced Search >>

    GET CITATION

    shu

    Export: BibTex EndNote

    Article Metrics

    Article views: 2942 Times PDF downloads: 30 Times Cited by: 0 Times

    History

    Received: 13 December 2014 Revised: Online: Published: 01 June 2015

    Catalog

      Email This Article

      User name:
      Email:*请输入正确邮箱
      Code:*验证码错误
      Send
      Article Navigation >  Journal of Semiconductors  > 2015  >  36(6): 064003
      S. Theodore Chandra, N. B. Balamurugan, M. Bhuvaneswari, N. Anbuselvan, N. Mohankumar. Analysis of charge density and Fermi level of AlInSb/InSb single-gate high electron mobility transistor[J]. Journal of Semiconductors, 2015, 36(6): 064003. doi: 10.1088/1674-4926/36/6/064003 ****S. T. Chandra, N. B. Balamurugan, M. Bhuvaneswari, N. Anbuselvan, N. Mohankumar. Analysis of charge density and Fermi level of AlInSb/InSb single-gate high electron mobility transistor[J]. J. Semicond., 2015, 36(6): 064003. doi:  10.1088/1674-4926/36/6/064003.
      Citation:
      S. Theodore Chandra, N. B. Balamurugan, M. Bhuvaneswari, N. Anbuselvan, N. Mohankumar. Analysis of charge density and Fermi level of AlInSb/InSb single-gate high electron mobility transistor[J]. Journal of Semiconductors, 2015, 36(6): 064003. doi: 10.1088/1674-4926/36/6/064003 ****
      S. T. Chandra, N. B. Balamurugan, M. Bhuvaneswari, N. Anbuselvan, N. Mohankumar. Analysis of charge density and Fermi level of AlInSb/InSb single-gate high electron mobility transistor[J]. J. Semicond., 2015, 36(6): 064003. doi:  10.1088/1674-4926/36/6/064003.
      shu

      Analysis of charge density and Fermi level of AlInSb/InSb single-gate high electron mobility transistor

      DOI: 10.1088/1674-4926/36/6/064003

      • National Instruments Electronics Laboratory, Department of ECE, Thiagarajar College of Engineering, Madurai, Tamilnadu, India

      Funds:

      Project supported by the Council of Scientific & Industrial Research (CSIR), India under the Senior Research Fellowship Scheme (No. 08/237(0005)/2012-EMR-I).

      More Information
      • Corresponding author: E-amil: theodore@tce.edu
      • Received Date: 2014-12-13
      • Accepted Date: 2015-01-21
      • Published Date: 2015-01-25

      Catalog

        Journal of Semiconductors © 2017 All Rights Reserved   京ICP备05085259号-2

        /

        DownLoad:  Full-Size Img  PowerPoint
        Return
        Return