| Citation: |
Qiang Yao, Zuochang Ye, Wenjian Yu. An efficient method for comprehensive modeling and parasitic extraction of cylindrical through-silicon vias in 3D ICs[J]. Journal of Semiconductors, 2015, 36(8): 085006. doi: 10.1088/1674-4926/36/8/085006
****
Q Yao, Z C Ye, W J Yu. An efficient method for comprehensive modeling and parasitic extraction of cylindrical through-silicon vias in 3D ICs[J]. J. Semicond., 2015, 36(8): 085006. doi: 10.1088/1674-4926/36/8/085006.
|
An efficient method for comprehensive modeling and parasitic extraction of cylindrical through-silicon vias in 3D ICs
DOI: 10.1088/1674-4926/36/8/085006
More Information
-
Abstract
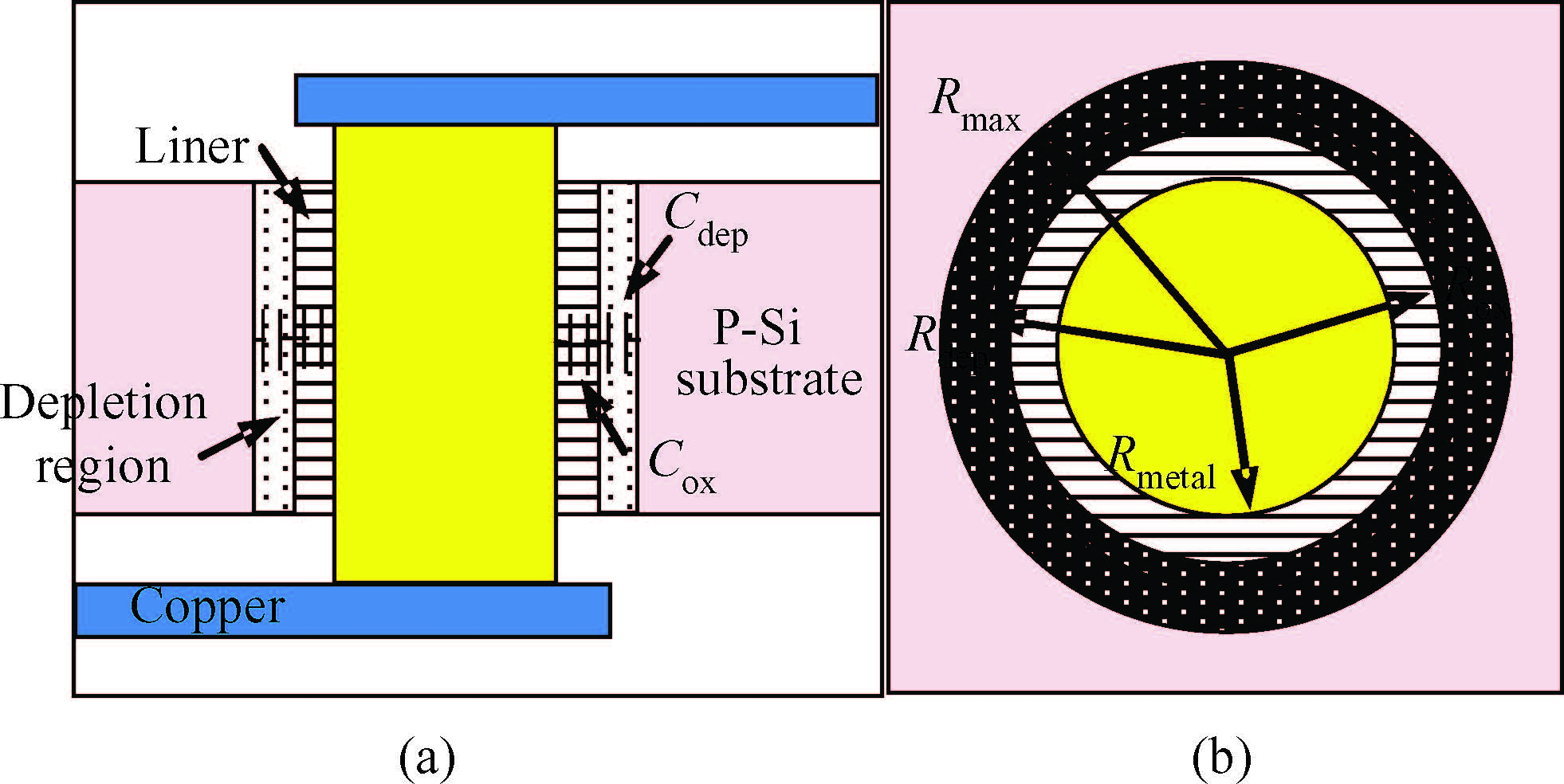
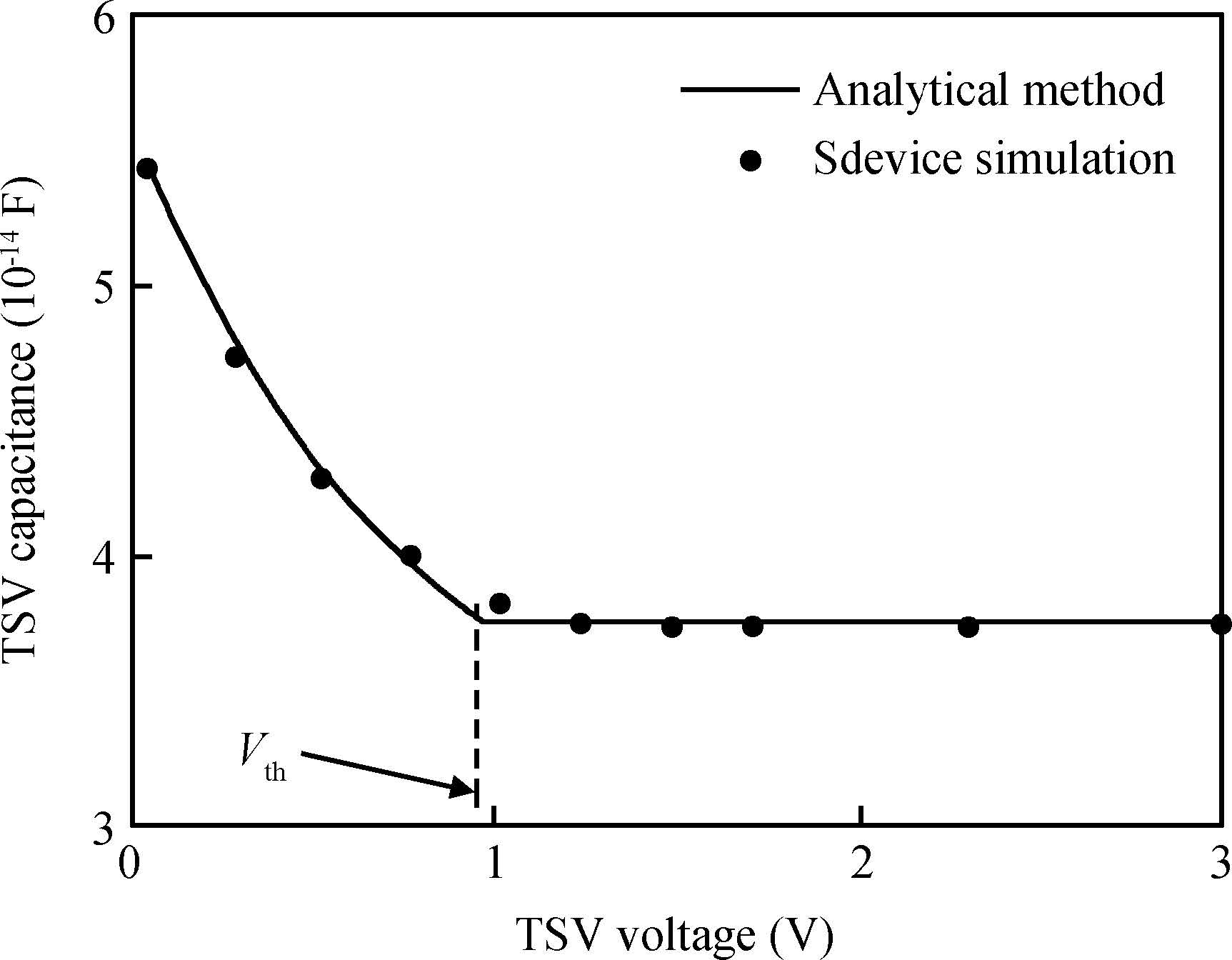
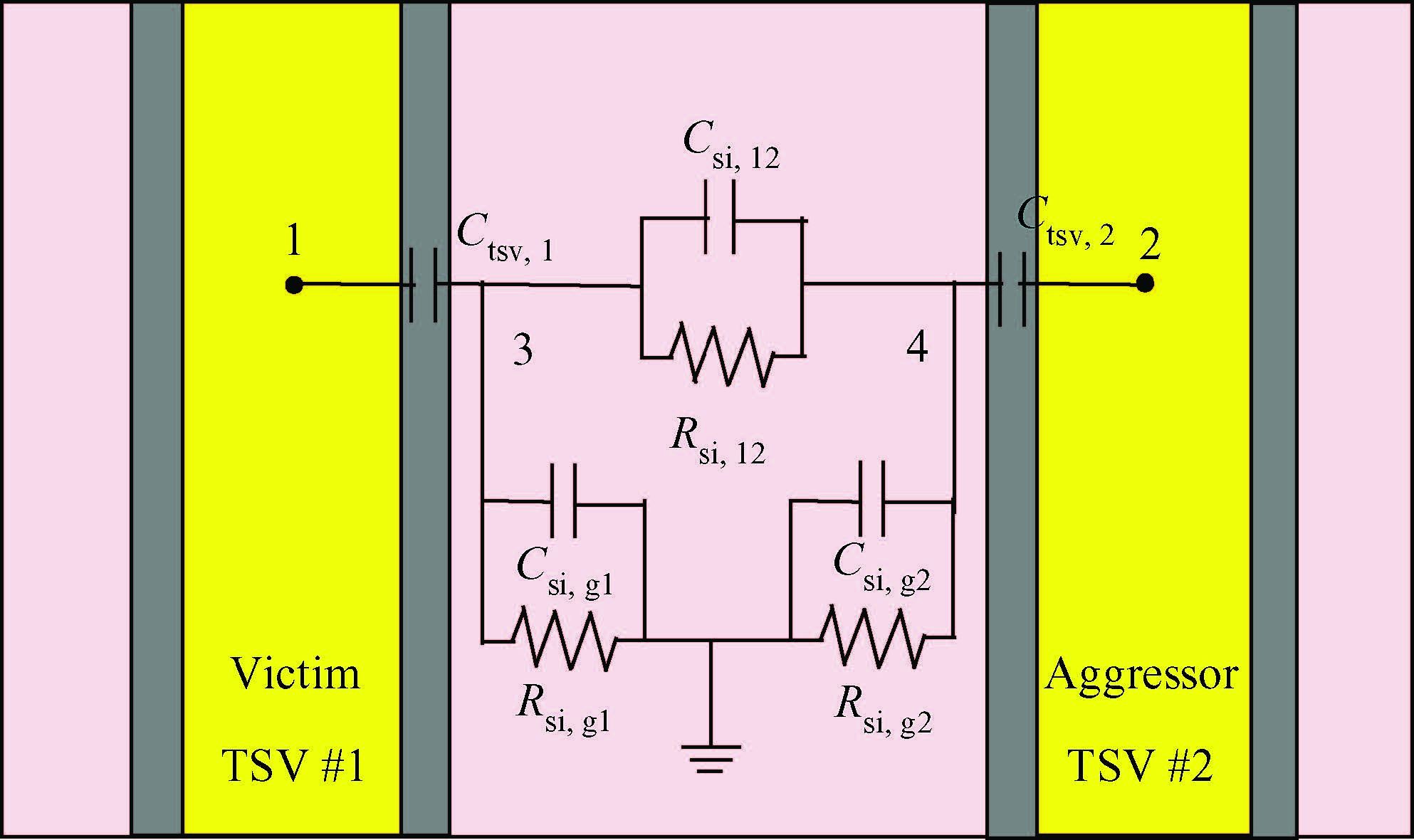
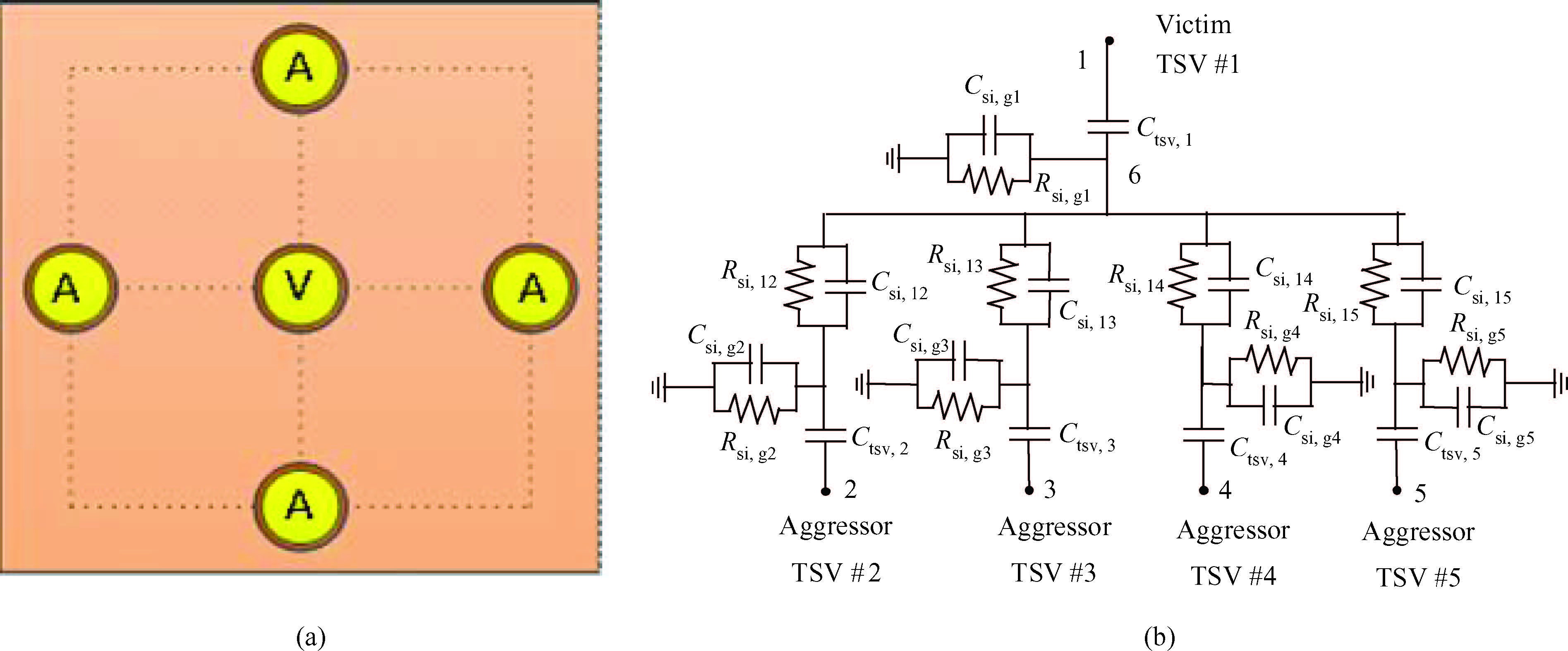
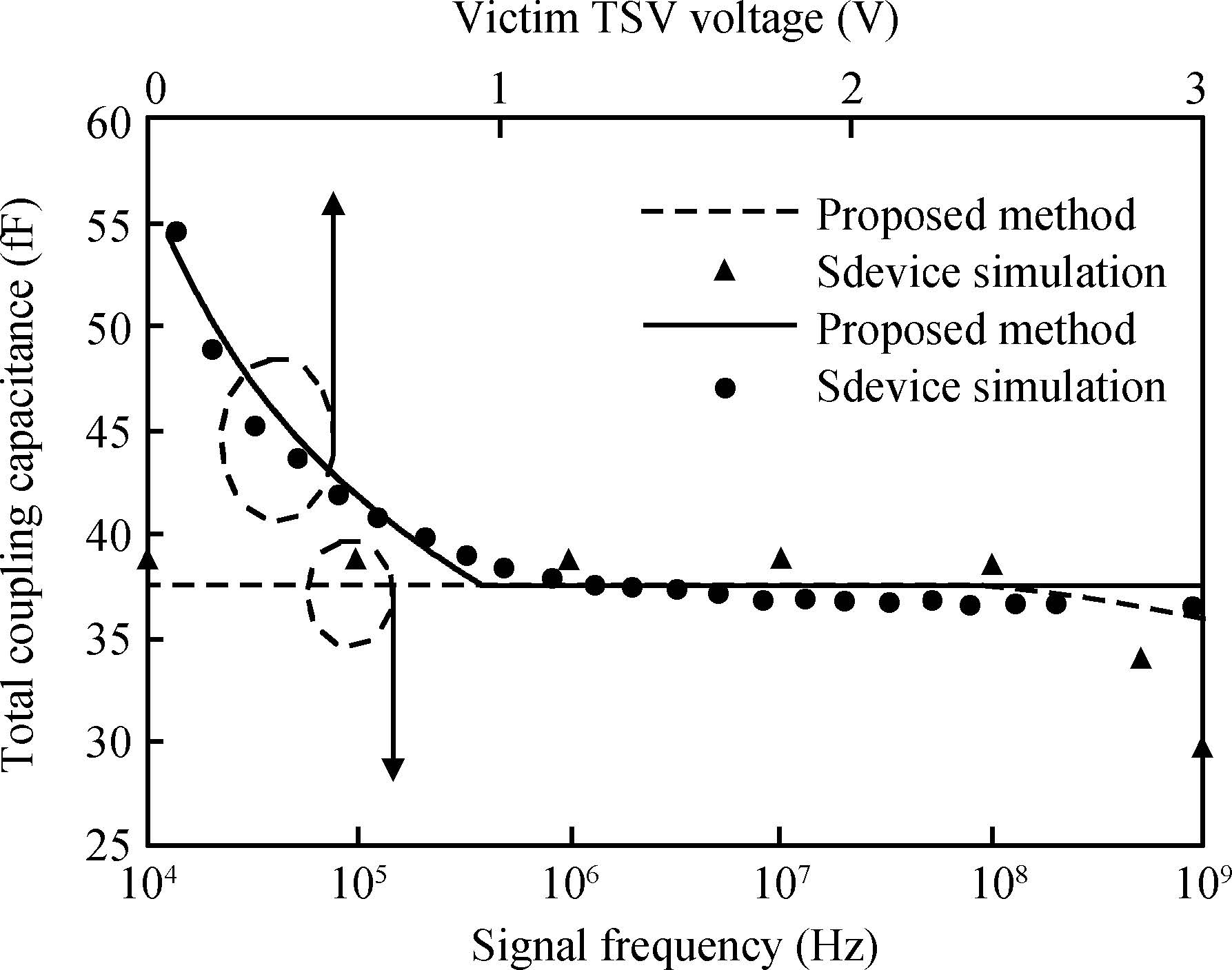
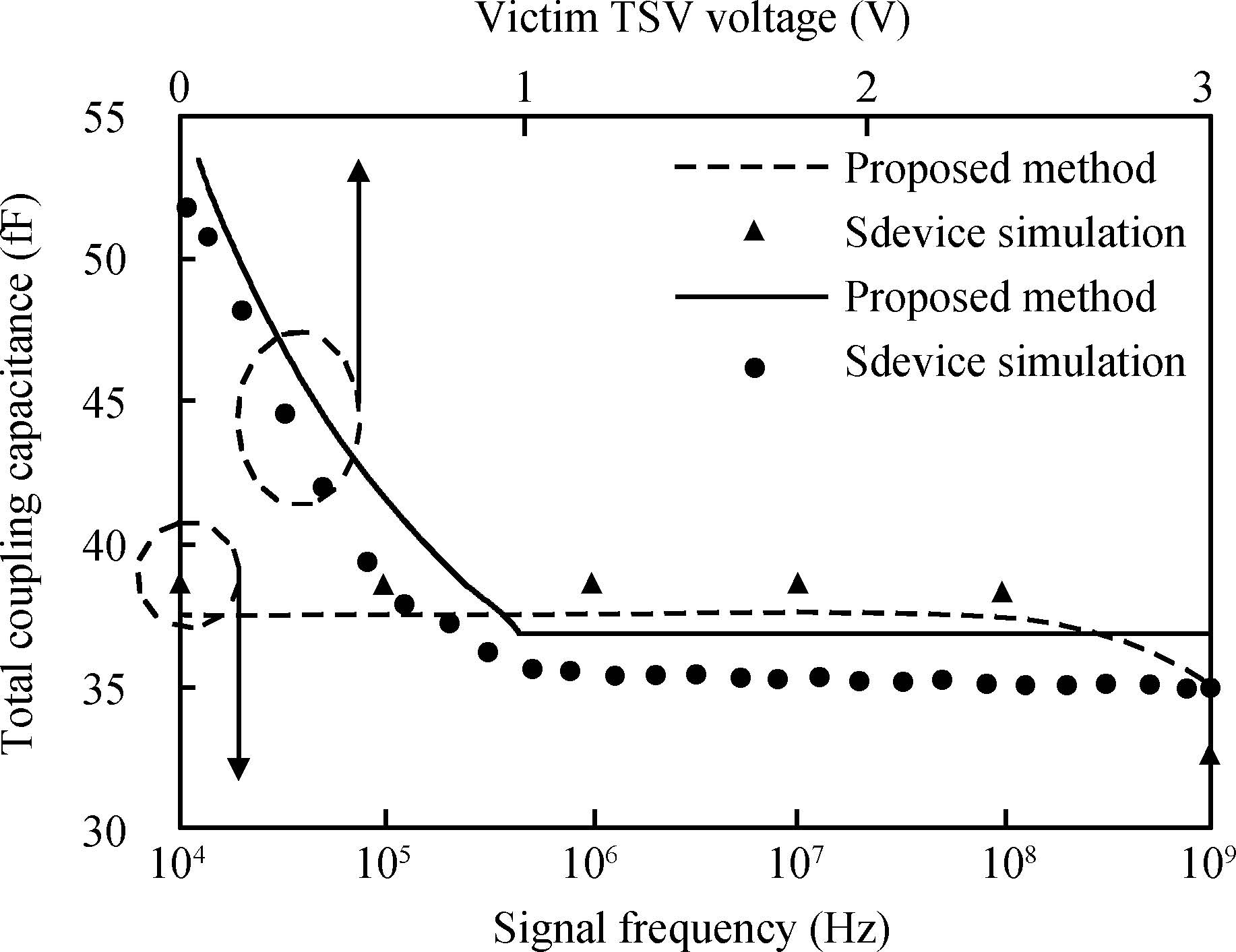
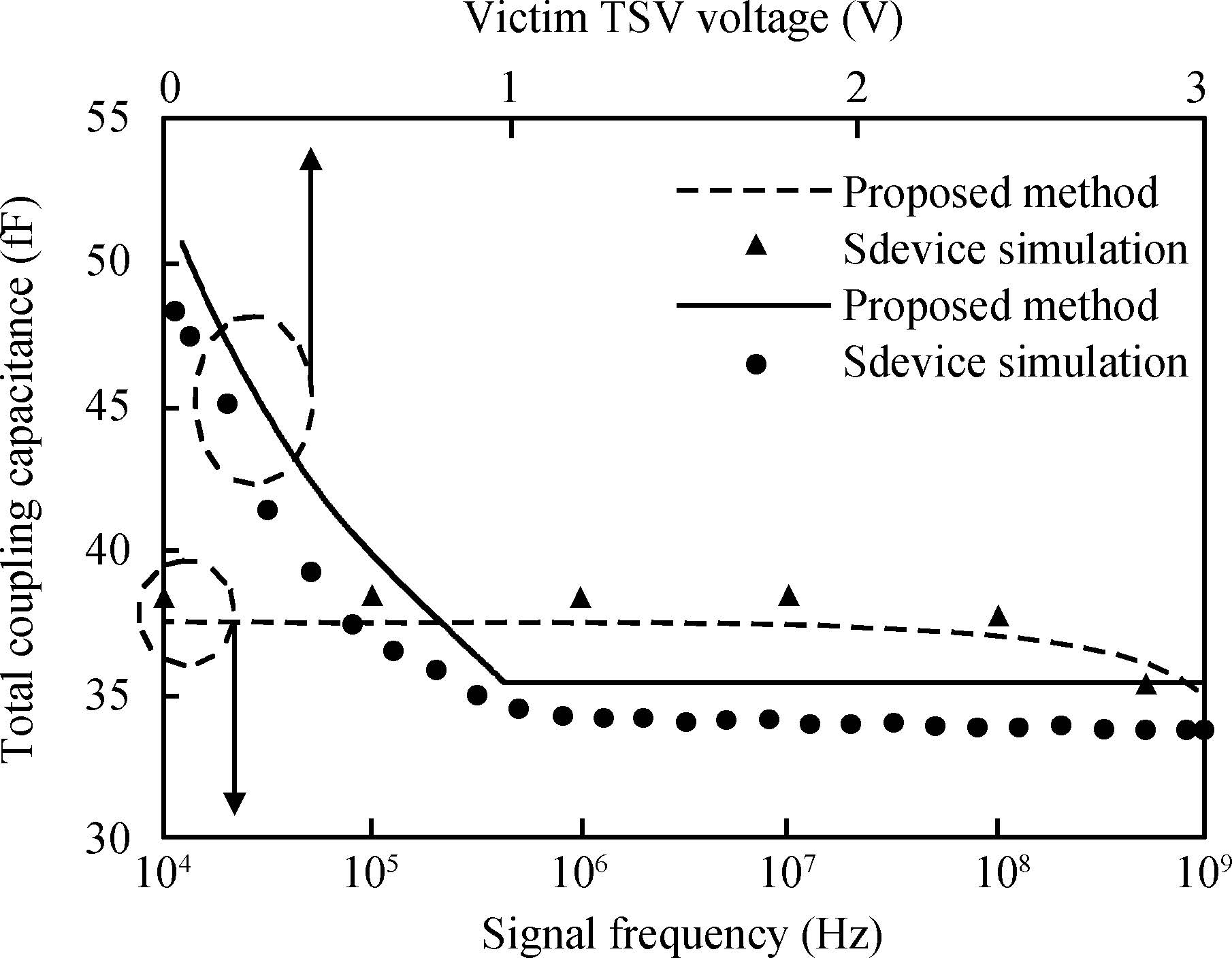
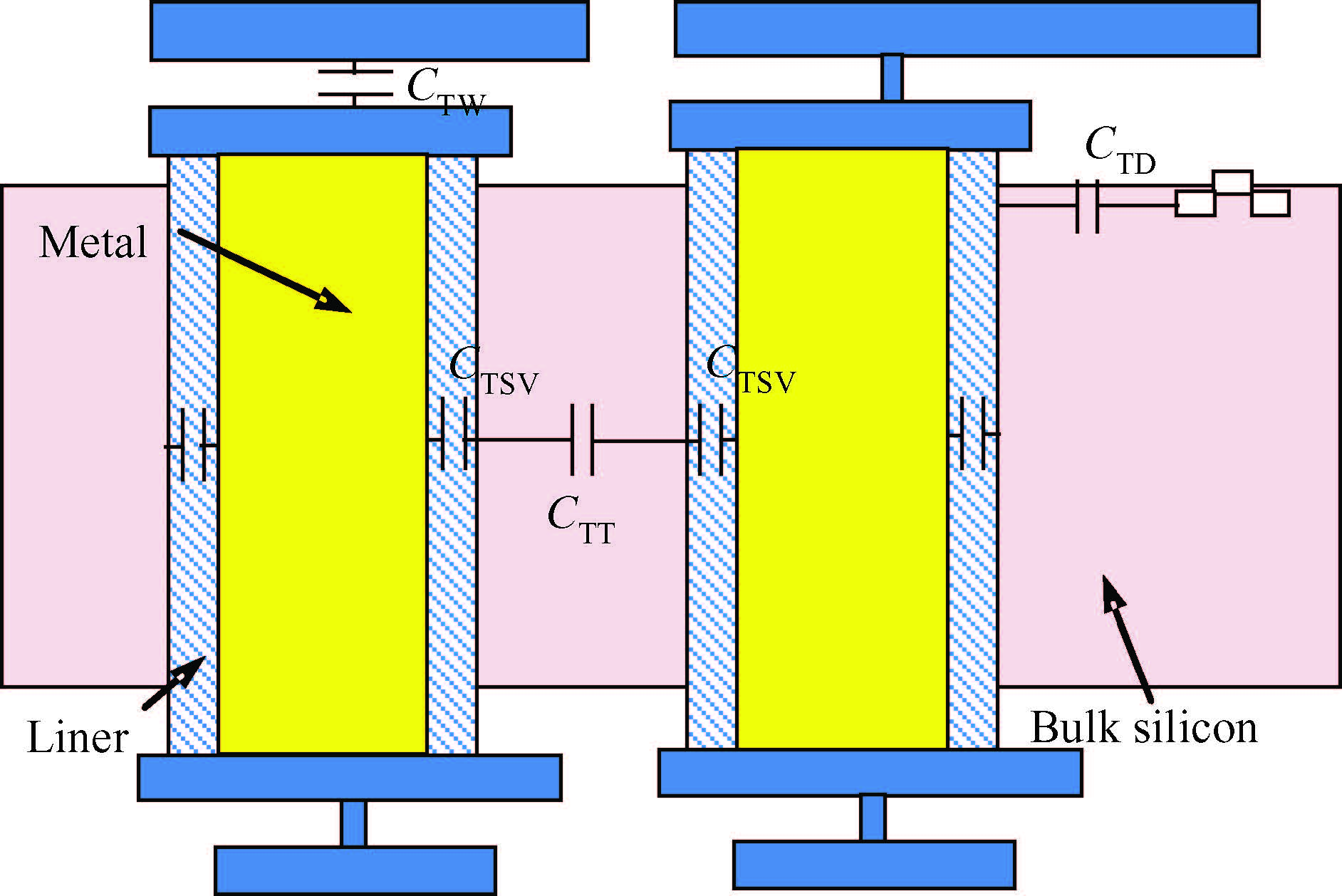
To build an accurate electric model for through-silicon vias (TSVs) in 3D integrated circuits (ICs), a resistance and capacitance (RC) circuit model and related efficient extraction technique are proposed. The circuit model takes both semiconductor and electrostatic effects into account, and is valid for low and medium signal frequencies. The electrostatic capacitances are extracted with a floating random walk based algorithm, and are then combined with the voltage-dependent semiconductor capacitances to form the equivalent circuit. Compared with the method used in Synopsys's Sdevice, which completely simulates the electro/semiconductor effects, the proposed method is more efficient and is able to handle the general TSV layout as well. For several TSV structures, the experimental results validate the accuracy of the proposed method for the frequency range from 10 kHz to 1 GHz. The proposed method demonstrated 47× speedup over the Sdevice for the largest 9-TSV case. -
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] -
Proportional views





 DownLoad:
DownLoad: