Energy levels of magneto-optical polaron in spherical quantum dot——Part 1: Strong coupling

A. J. Fotue; S. C. Kenfack; N. Issofa; M. Tiotsop; H. Fotsin; E. Mainimo; L. C.  Fai

doi:10.1088/1674-4926/36/9/092001

J. Semicond. > 2015, Volume 36 > Issue 9 > 092001

SEMICONDUCTOR PHYSICS

Energy levels of magneto-optical polaron in spherical quantum dot——Part 1: Strong coupling

A. J. Fotue¹, S. C. Kenfack¹, N. Issofa¹, M. Tiotsop¹, H. Fotsin², E. Mainimo¹ and L. C. Fai¹

+ Author Affiliations

Corresponding author: A.J.Fotue,

DOI: 10.1088/1674-4926/36/9/092001

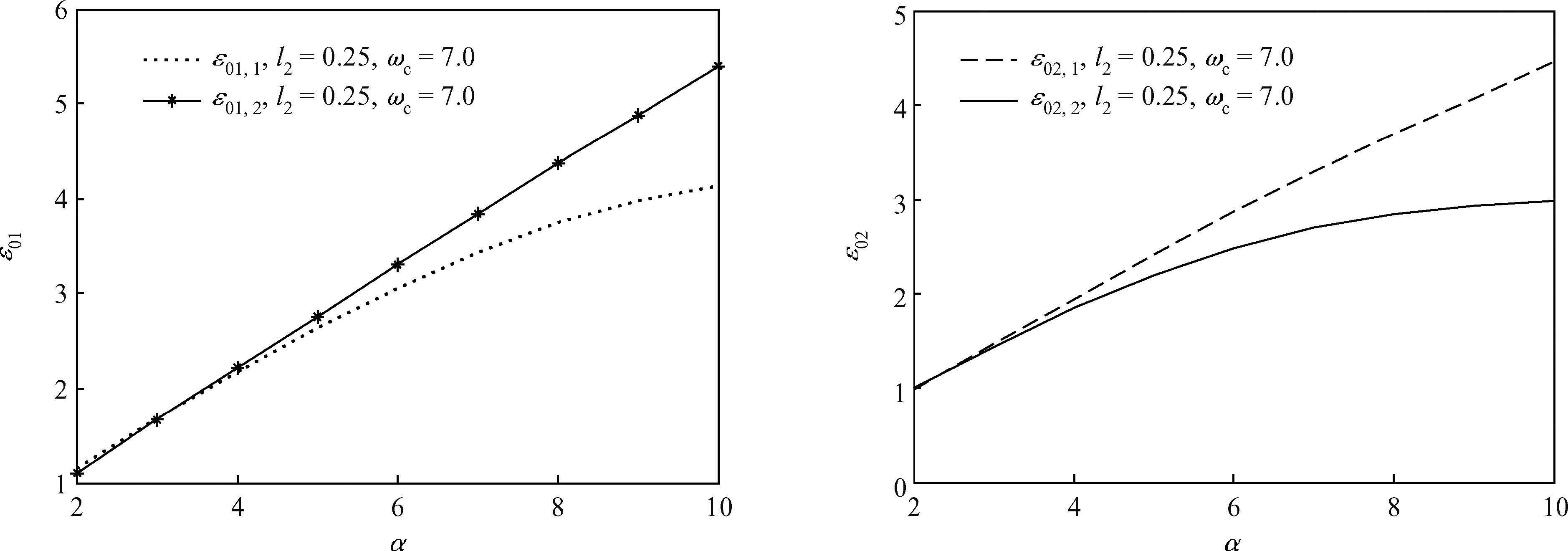
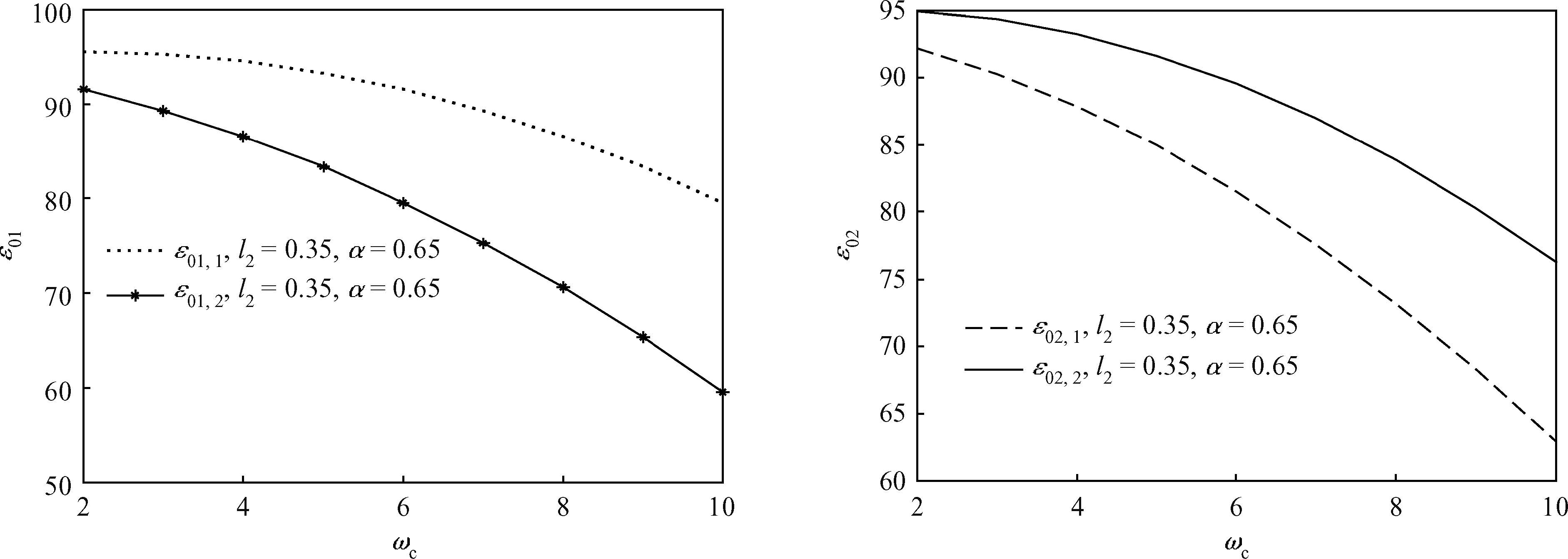
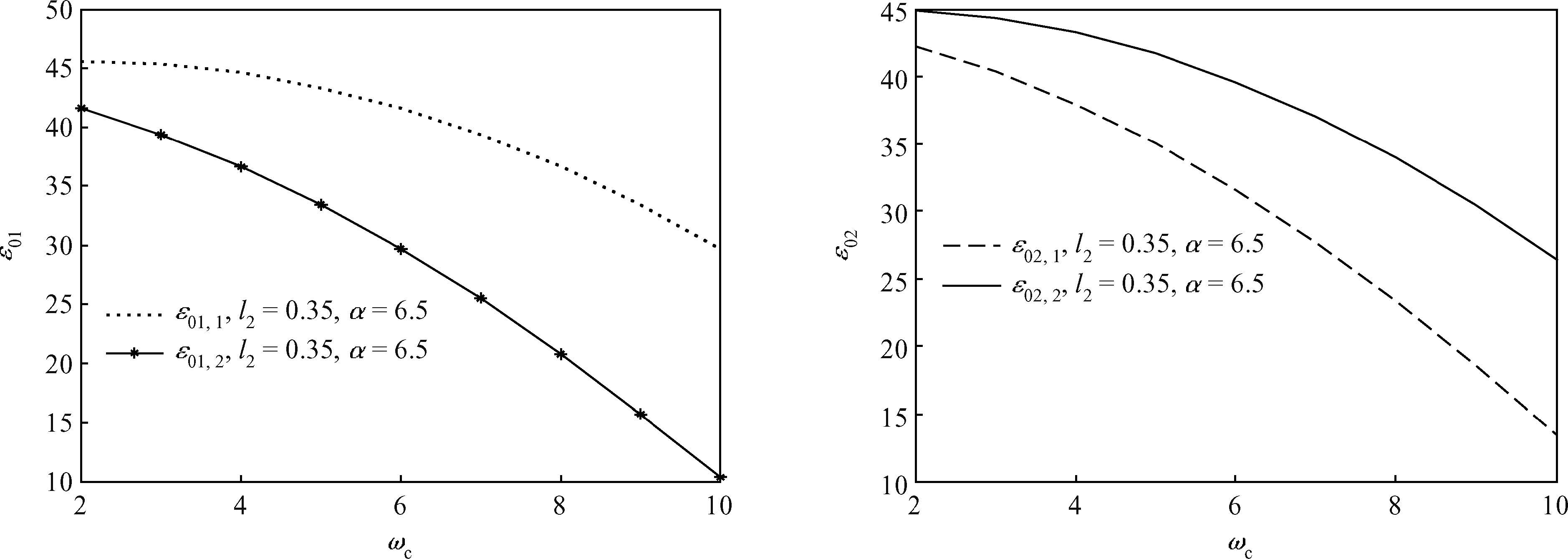
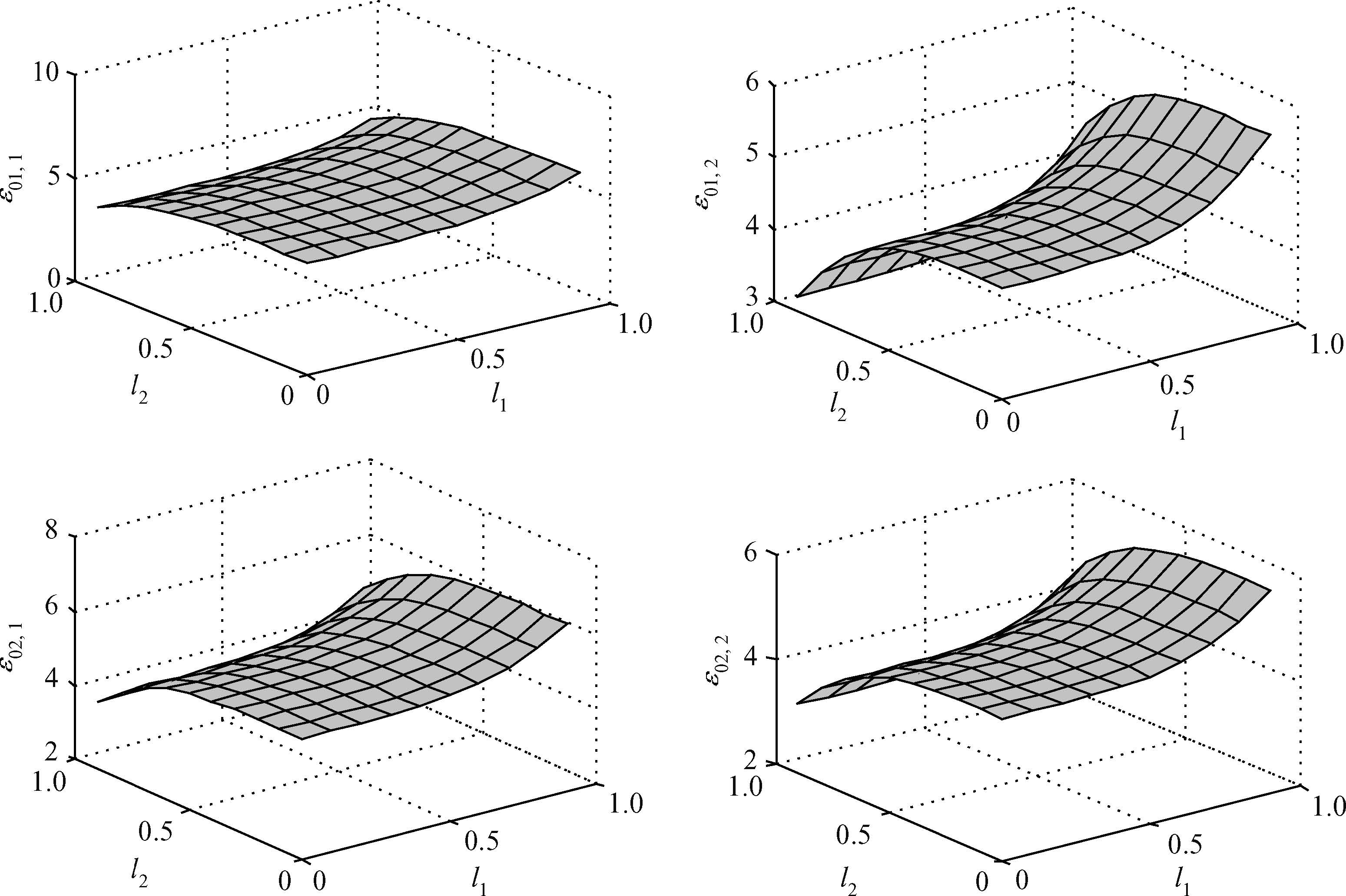
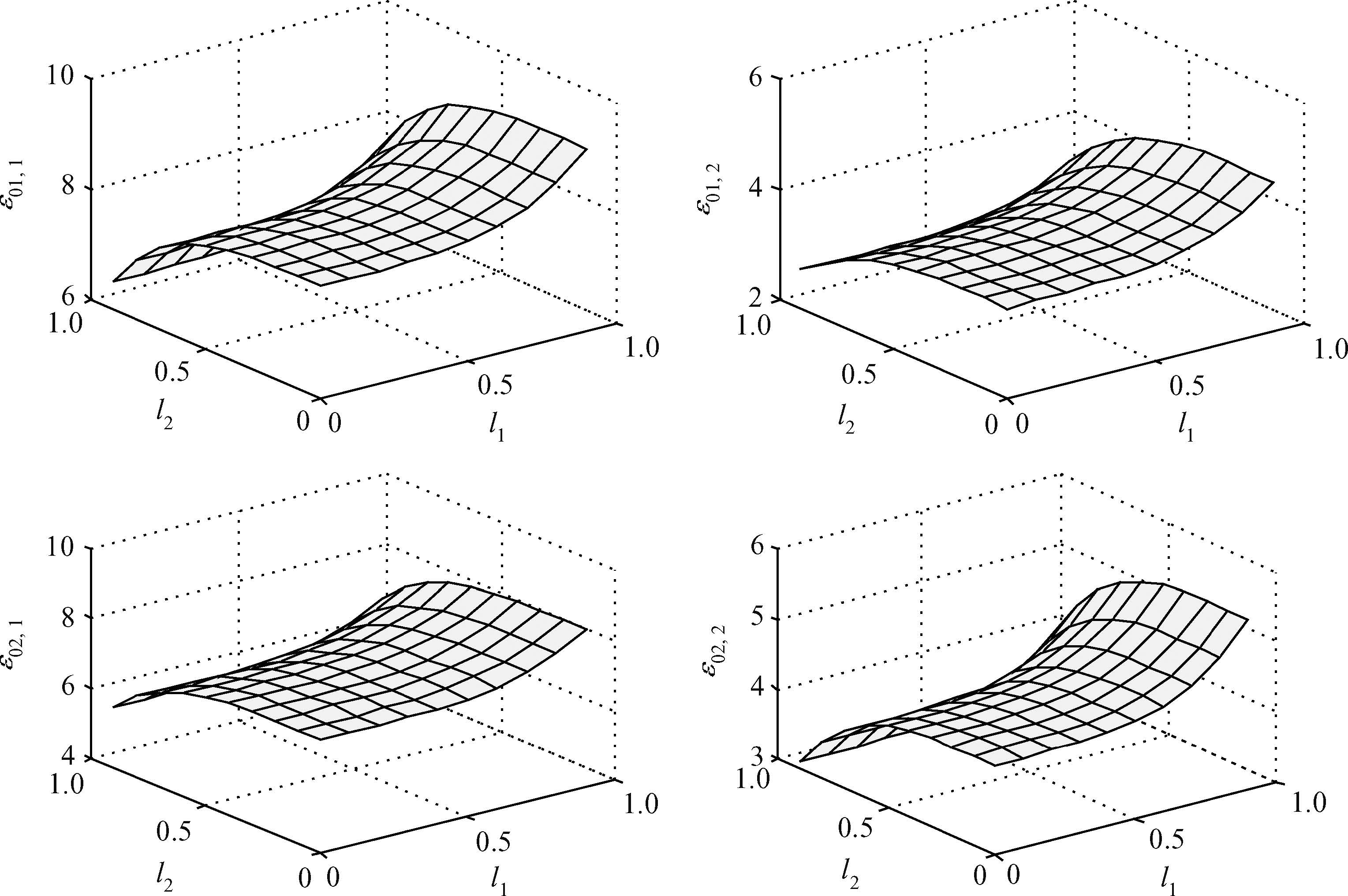
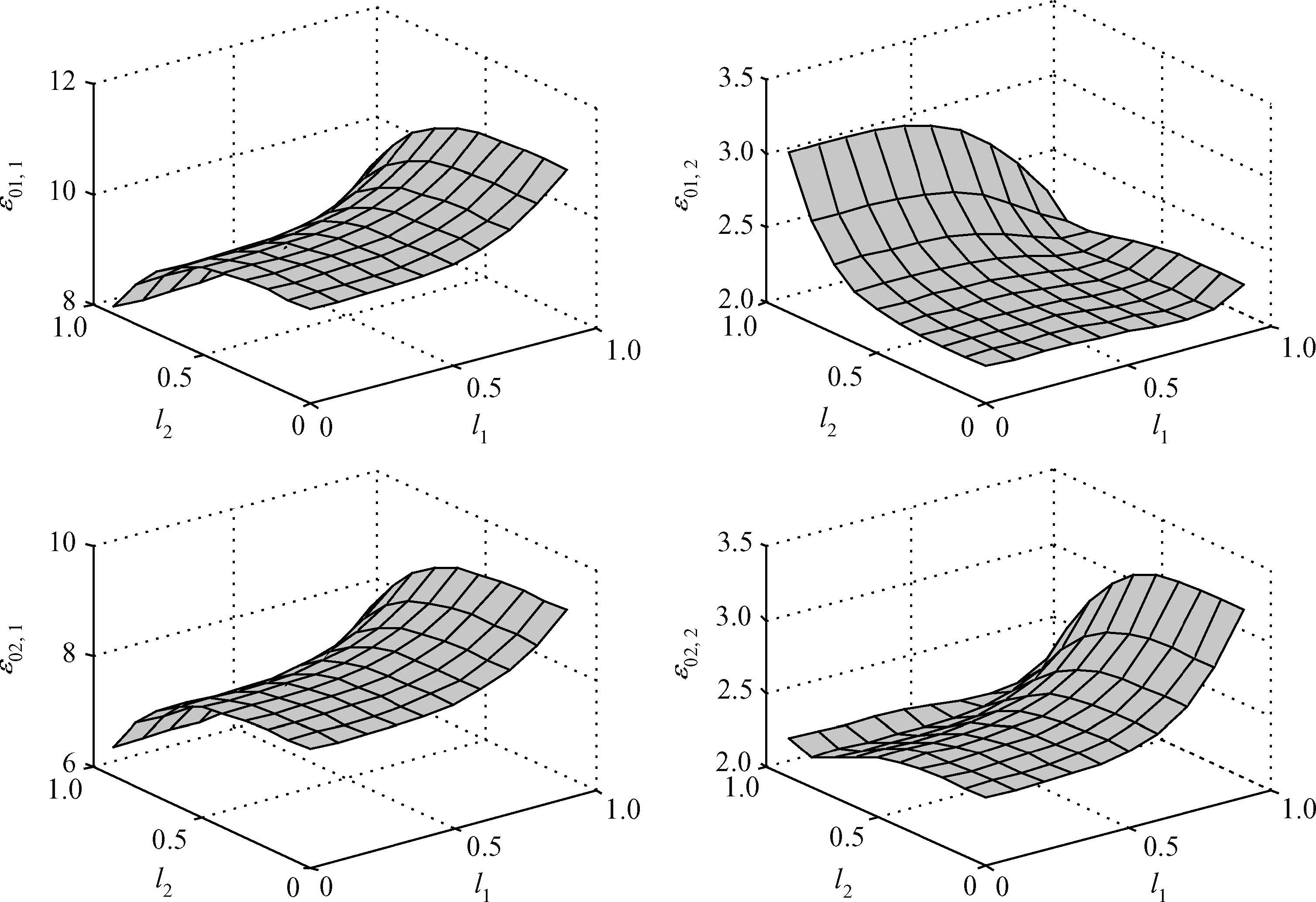
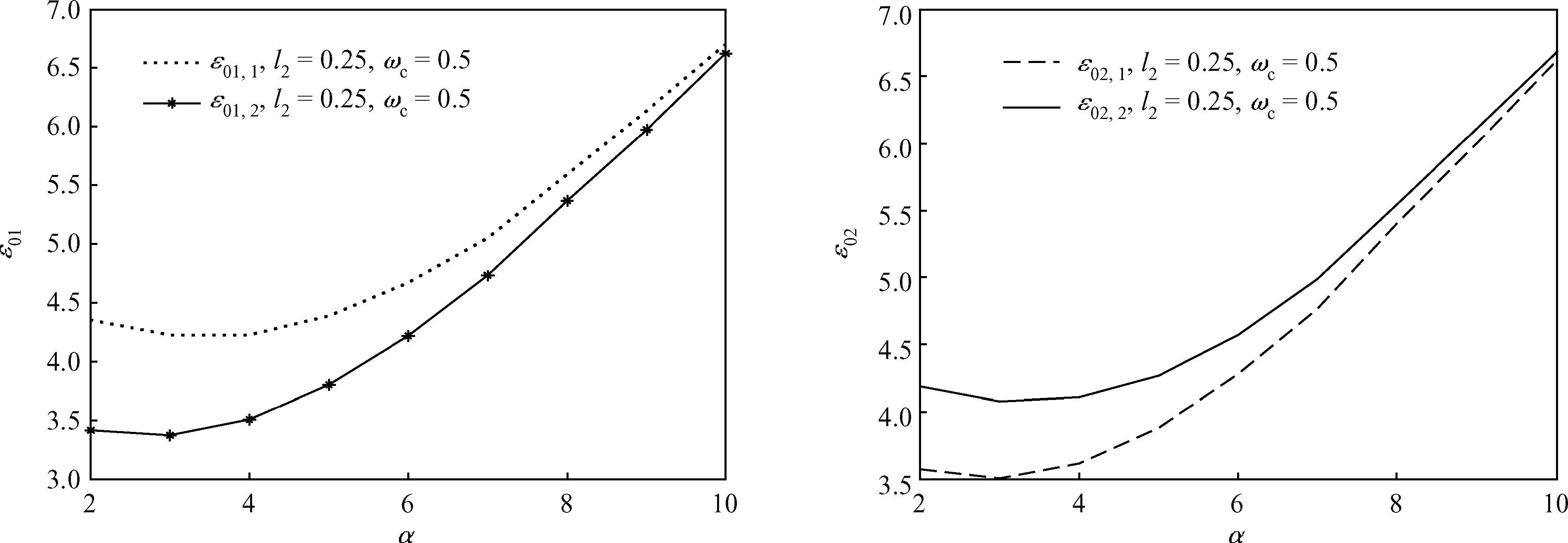
Abstract: We investigate the influence of a magnetic field on the ground state energy of a polaron in a spherical semiconductor quantum dot (QD) using the modified LLP method. The ground state energy is split into sub-energy levels and there is a degeneracy of energy levels. It is also observed that the degenerate energy increase with the electron-phonon coupling constant and decrease with the magnetic field. The numerical results show that, under the influence of magnetic field and the interaction with the total momentum along the z-direction, the split energy increases and decreases with the longitudinal and the transverse confinement length, respectively.

Key words: magnetic field, total momentum, modified LLP, polaron energy, quantum dot

References

[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]
[26]
[27]
[28]
[29]
[30]
[31]
[32]
[33]
[34]
[35]
[36]
[37]
[38]
[39]
[40]
[41]
[42]
[43]
[44]
[45]
[46]
[47]

Fig. 1. Splitting ground state energies of polaron in 1S state as function of coupling constant α with l₁=0.55, l₂=0.25 and ω_c=0.5.

DownLoad: Full-Size Img PowerPoint

Fig. 2. Splitting ground state energies of polaron in 1S state as function of coupling constant α withl₁=0.55, l₂=0.25 and ω_c=7.0.

DownLoad: Full-Size Img PowerPoint

Fig. 3. Splitting ground state energies of polaron in 1S state as function of cyclotron frequency constant ω_c with l₁=0.25,l₂=0.35 and α=6.5.

DownLoad: Full-Size Img PowerPoint

Fig. 4. Splitting ground state energies of polaron in 1S state as function of cyclotron frequency constant ω_c with l₁=0.30,l₂=0.35 and α=6.5.

DownLoad: Full-Size Img PowerPoint

Fig. 5. Splitting ground state energies of polaron in 1S state as function of confinement length l₁ and l₂ with α =6.5 and ω_c=0.5.

DownLoad: Full-Size Img PowerPoint

Fig. 6. Splitting ground state energies of polaron in 1S state as function confinement length l₁ and l₂ with α =6.5 and ω_c=2.0.

DownLoad: Full-Size Img PowerPoint

Fig. 7. Splitting ground state energies of polaron in 1S state as function of confinement length l₁ and l₂ with α =6.5 and ω_c=5.0.

DownLoad: Full-Size Img PowerPoint

DownLoad: CSV

[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]
[26]
[27]
[28]
[29]
[30]
[31]
[32]
[33]
[34]
[35]
[36]
[37]
[38]
[39]
[40]
[41]
[42]
[43]
[44]
[45]
[46]
[47]