| Citation: |
Yunfang Jia, Cheng Ju. Sentaurus® based modeling and simulation for GFET's characteristic for ssDNA immobilization and hybridization[J]. Journal of Semiconductors, 2016, 37(1): 014005. doi: 10.1088/1674-4926/37/1/014005
****
Y F Jia, C Ju. Sentaurus® based modeling and simulation for GFET\'s characteristic for ssDNA immobilization and hybridization[J]. J. Semicond., 2016, 37(1): 014005. doi: 10.1088/1674-4926/37/1/014005.
|
Sentaurus® based modeling and simulation for GFET's characteristic for ssDNA immobilization and hybridization
DOI: 10.1088/1674-4926/37/1/014005
More Information
-
Abstract
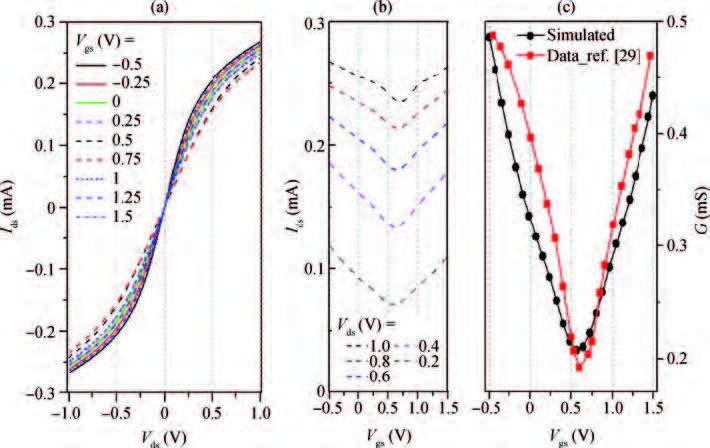
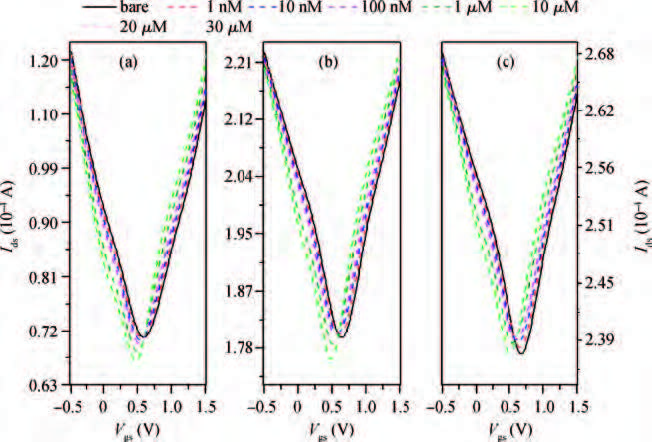
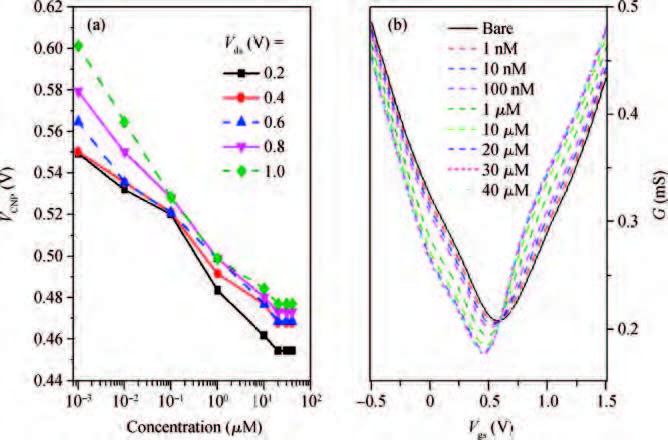
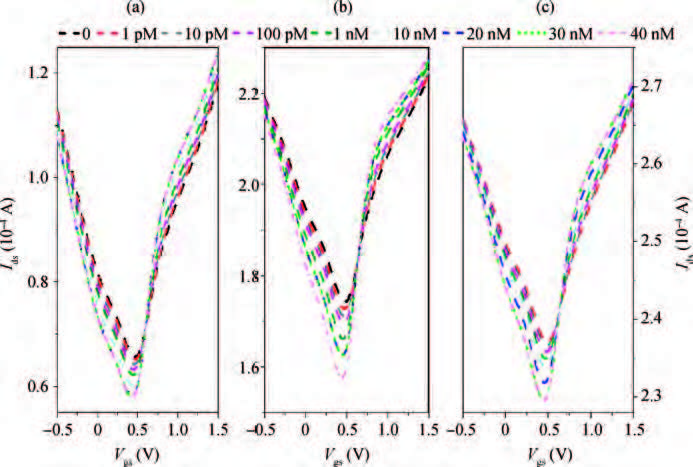
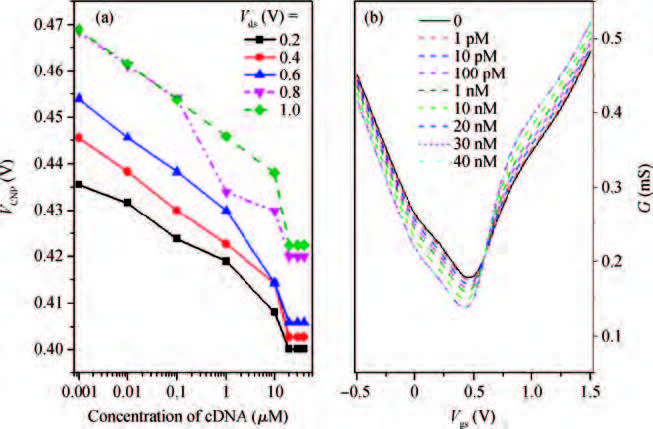
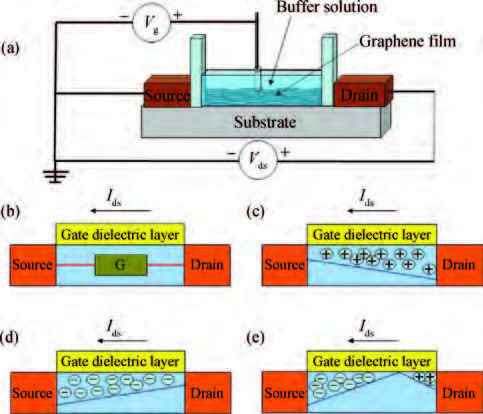
The graphene field effect transistor (GFET) has been widely studied and developed as sensors and functional devices. The first report about GFET sensing simulation on the device level is proposed. The GFET's characteristics, its responding for single strand DNA (ssDNA) and hybridization with the complimentary DNA (cDNA) are simulated based on Sentaurus, a popular CAD tool for electronic devices. The agreement between the simulated blank GFET feature and the reported experimental data suggests the feasibility of the presented simulation method. Then the simulations of ssDNA immobilization on GFET and hybridization with its cDNA are performed, the results are discussed based on the electron transfer (ET) mechanism between DNA and graphene.-
Keywords:
- graphene field effect transistor,
- DNA,
- simulation,
- electron transfer,
- Sentaurus
-
References
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] -
Proportional views





 DownLoad:
DownLoad: