J. Semicond. > 2016, Volume 37 > Issue 4 > 044004
|

SEMICONDUCTOR DEVICES

A physical model of hole mobility for germanium-on-insulator pMOSFETs

Wenyu Yuan, Jingping Xu, Lu Liu, Yong Huang and Zhixiang Cheng

+ Author Affiliations

 Corresponding author: Jingping Xu, Email:jpxu@hust.edu.cn

DOI: 10.1088/1674-4926/37/4/044004

PDF

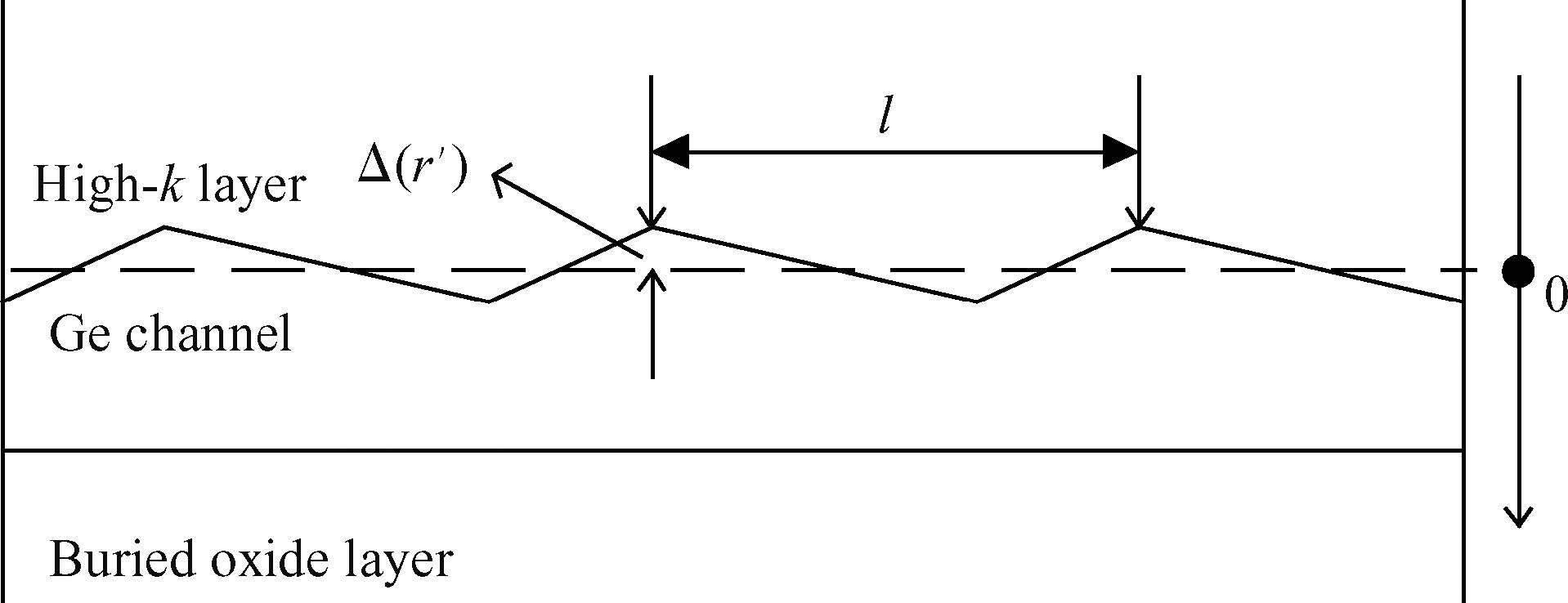
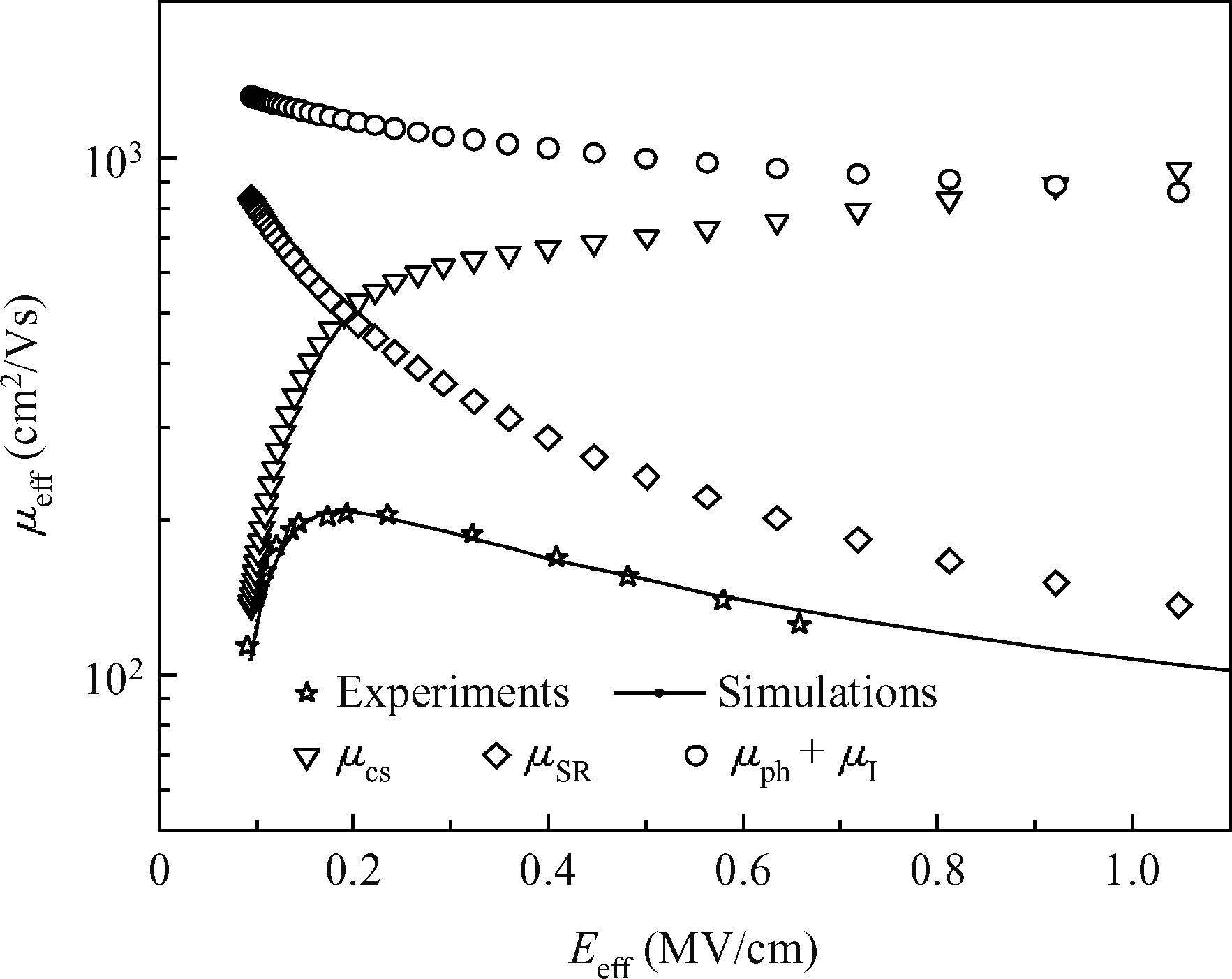
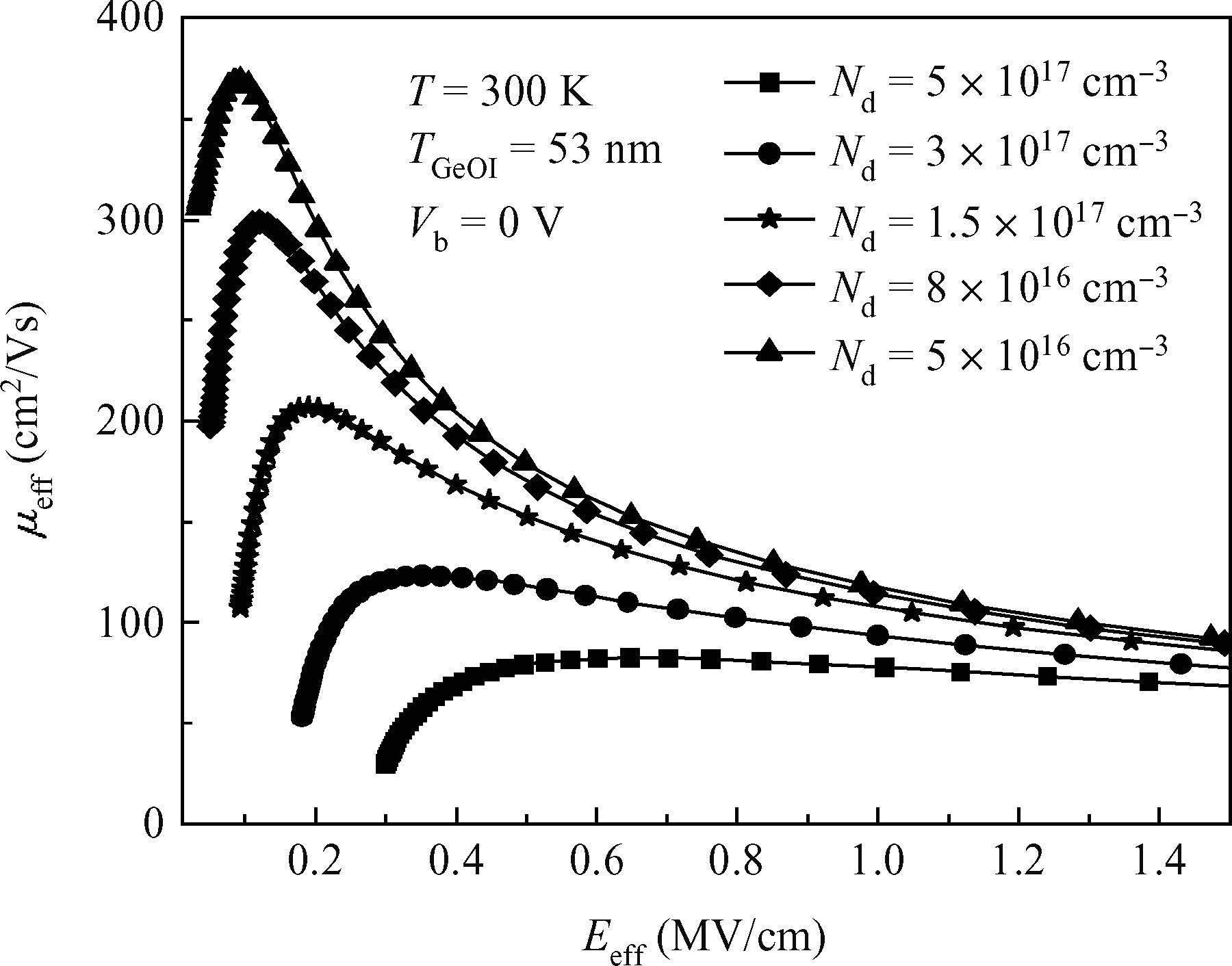
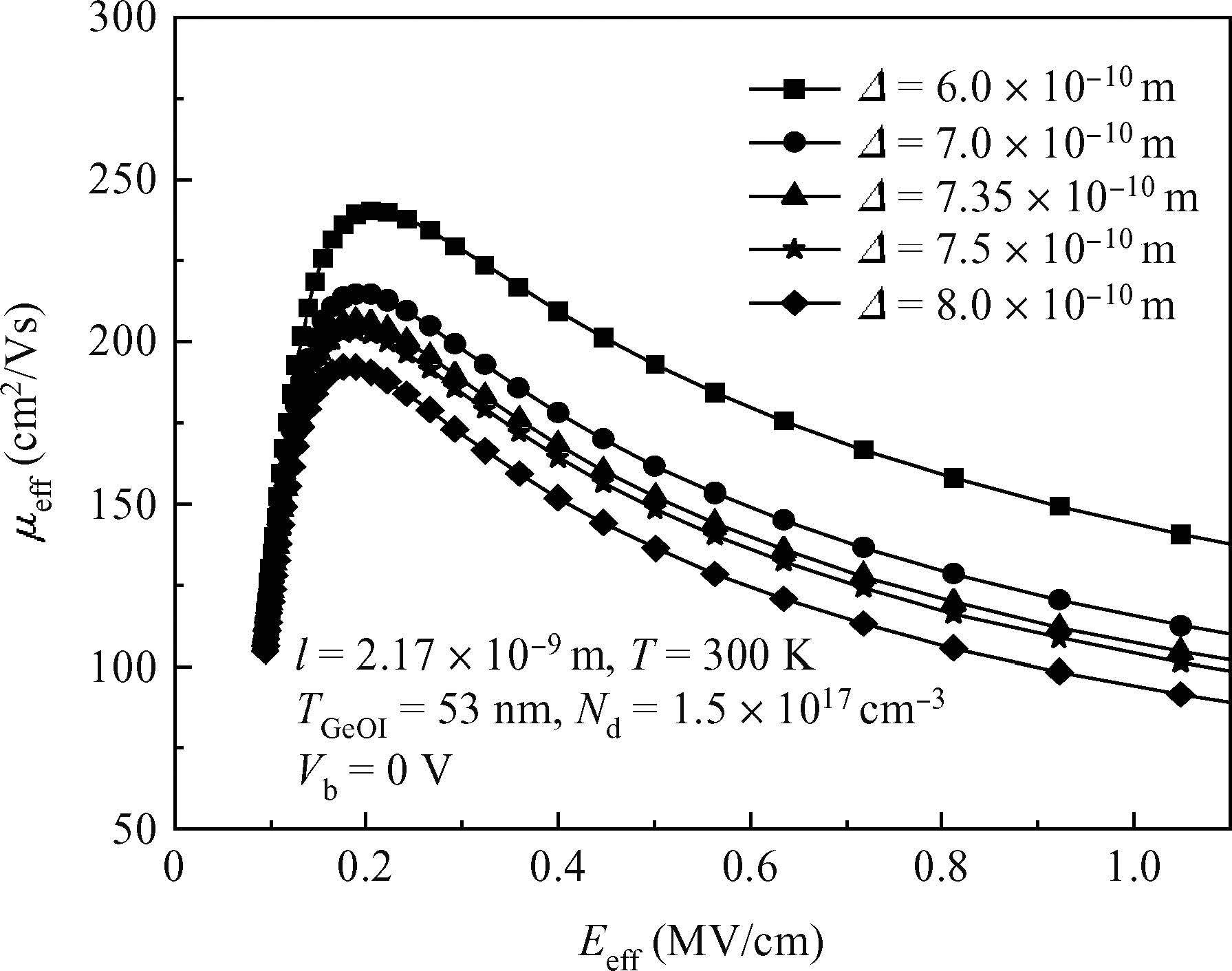
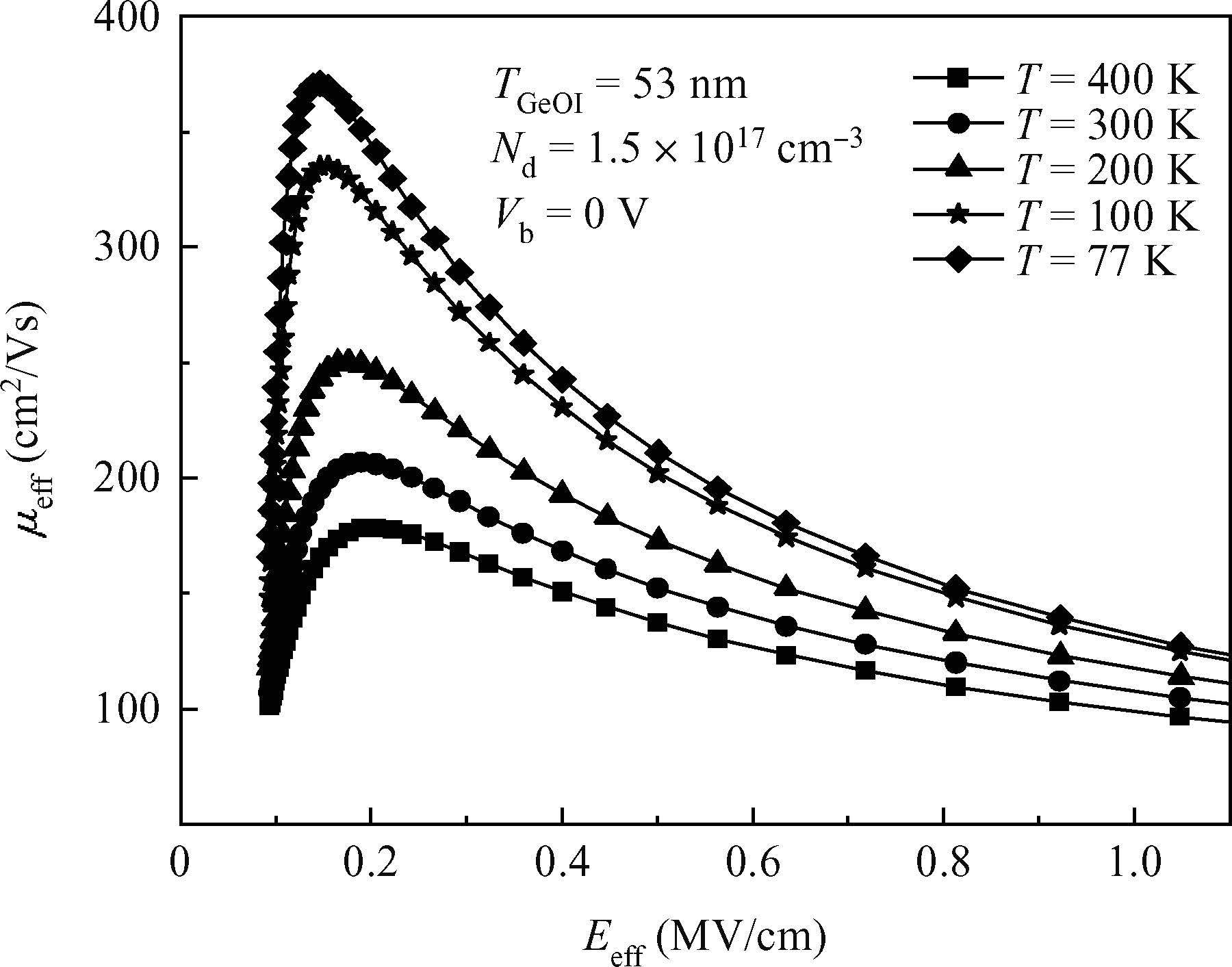
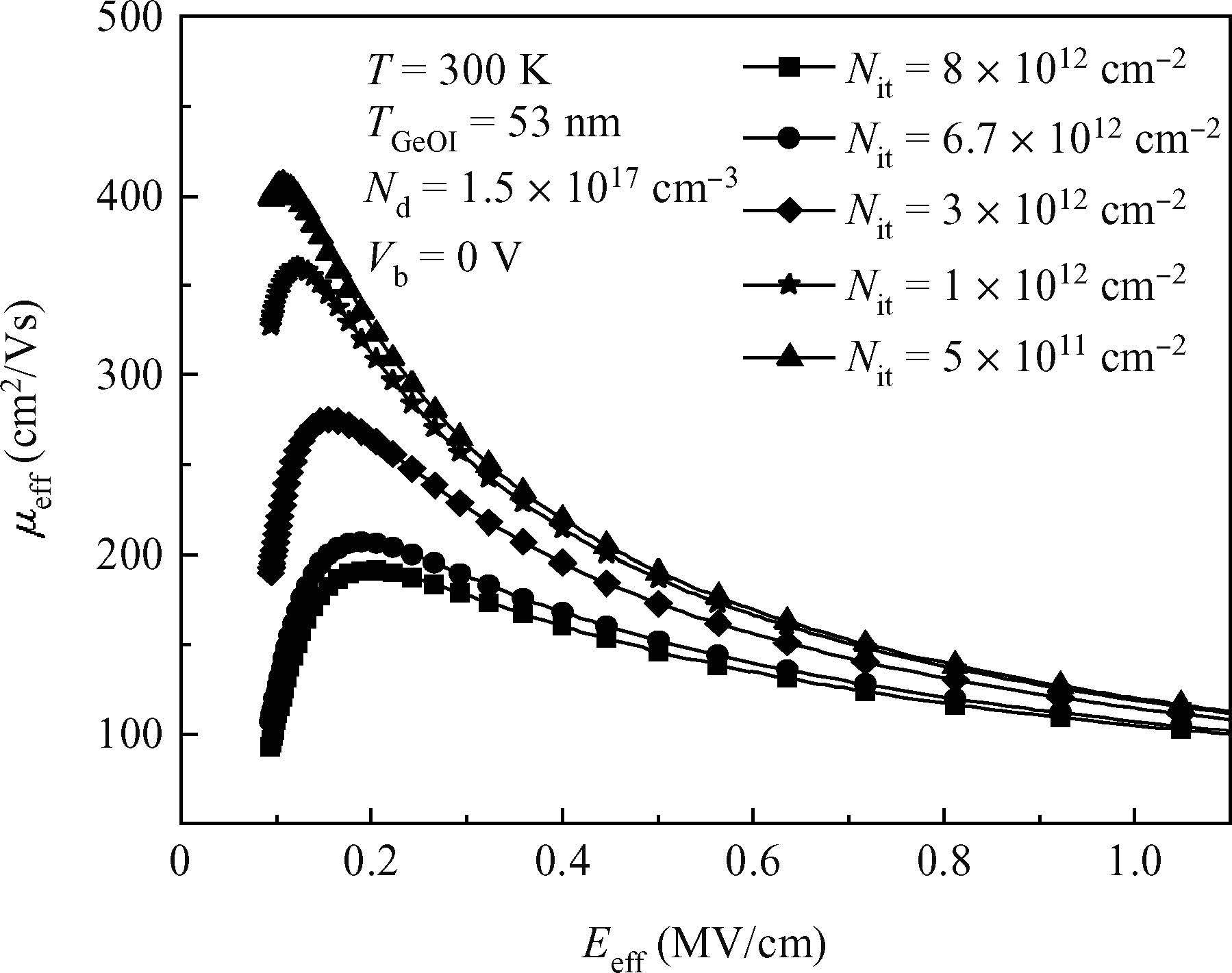
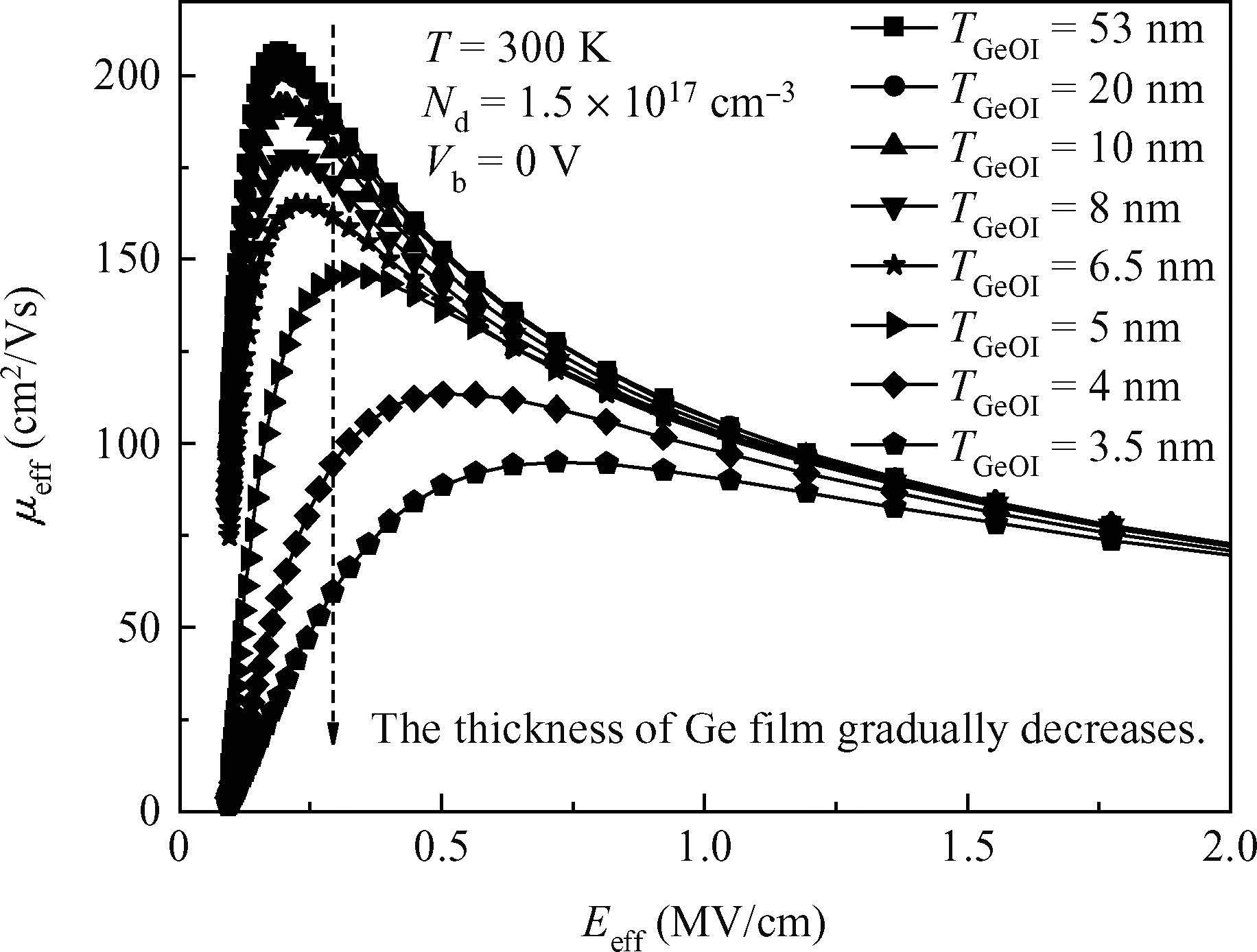
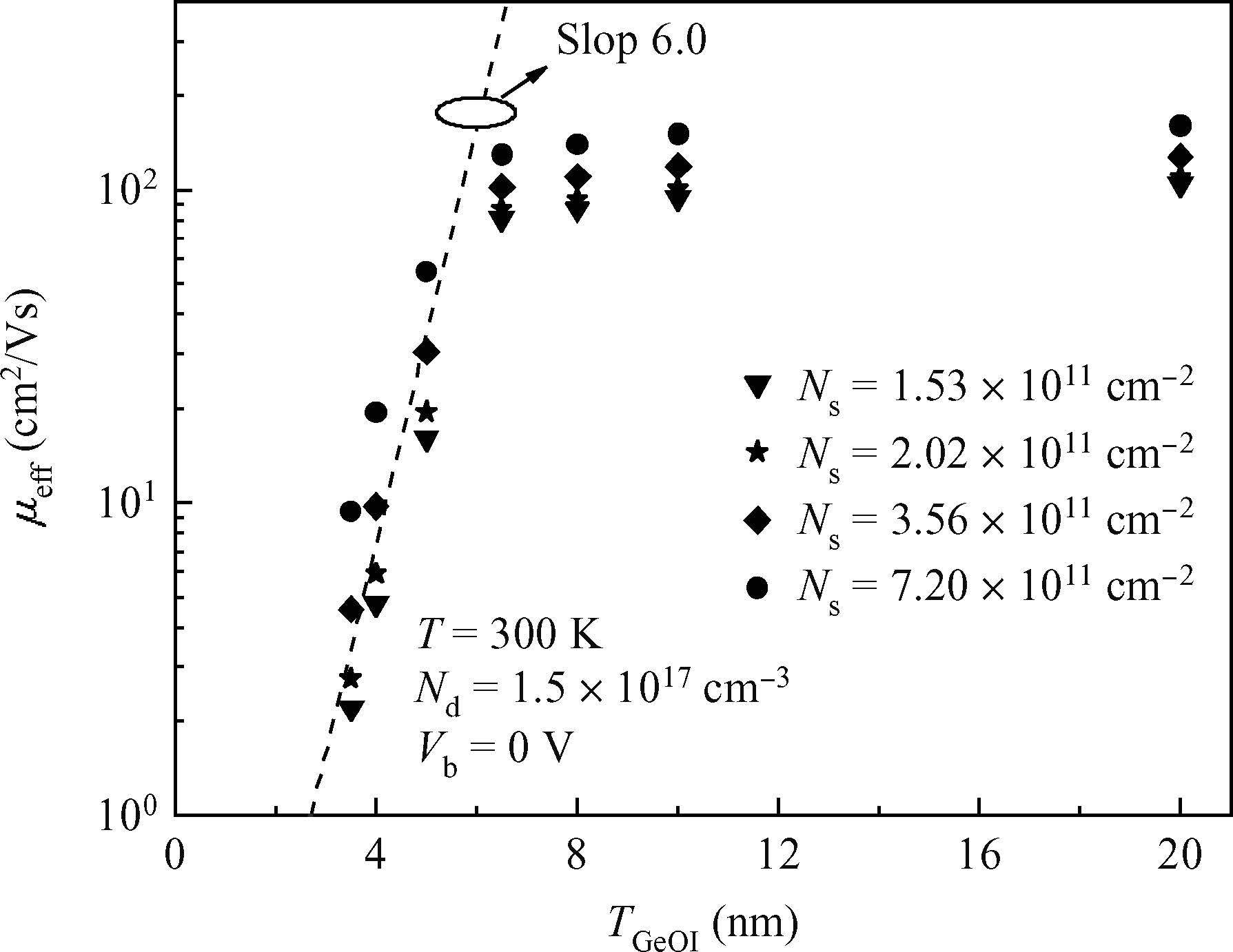
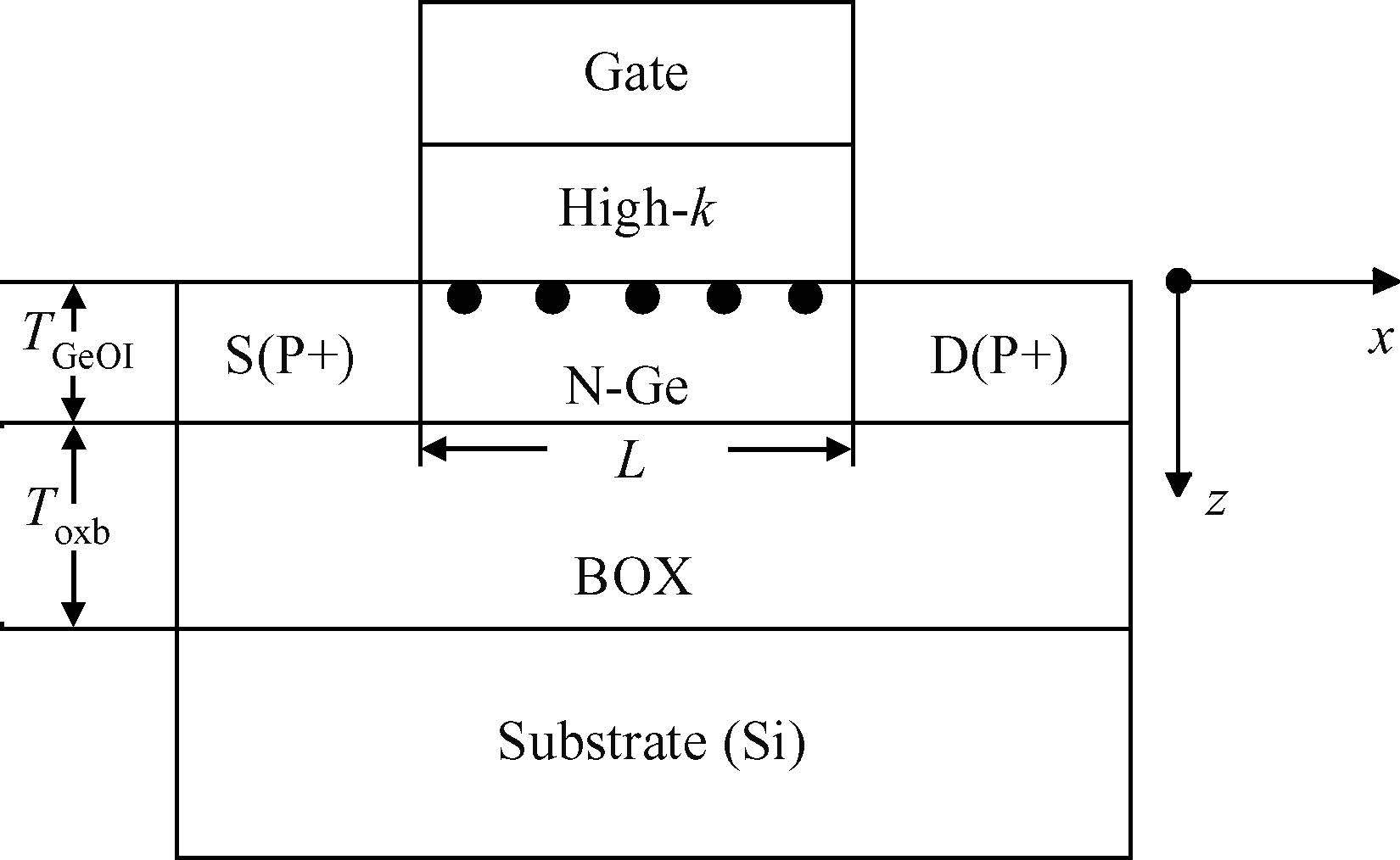
Abstract: A physical model of hole mobility for germanium-on-insulator pMOSFETs is built by analyzing all kinds of scattering mechanisms, and a good agreement of the simulated results with the experimental data is achieved, confirming the validity of this model. The scattering mechanisms involved in this model include acoustic phonon scattering, ionized impurity scattering, surface roughness scattering, coulomb scattering and the scattering caused by Ge film thickness fluctuation. The simulated results show that the coulomb scattering from the interface charges is responsible for the hole mobility degradation in the low-field regime and the surface roughness scattering limits the hole mobility in the high-field regime. In addition, the effects of some factors, e.g. temperature, doping concentration of the channel and the thickness of Ge film, on degradation of the mobility are also discussed using the model, thus obtaining a reasonable range of the relevant parameters.

Key words: GeOI, pMOSFETs, hole mobility, scattering mechanisms



[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]
[26]
[27]
[28]
[29]
[30]
[31]
[32]
Fig. 1.  The schematic diagram of a GeOI pMOSFET structure.

DownLoad: Full-Size Img PowerPoint
Fig. 2.  Schematic model for the roughness of the high-$k$ dielectric/Ge interface,in which the dashed line represents the average position of the interface.

DownLoad: Full-Size Img PowerPoint
Fig. 3.  Comparison between the simulated hole mobilities and the experimental data for GeOI pMOSFETs.

DownLoad: Full-Size Img PowerPoint
Fig. 4.  Hole mobility versus the effective electric field under different doping concentrations of the channel.

DownLoad: Full-Size Img PowerPoint
Fig. 5.  Hole mobility versus the effective electric field for various surface roughness.

DownLoad: Full-Size Img PowerPoint
Fig. 6.  Hole mobility versus the effective electric field under different temperatures.

DownLoad: Full-Size Img PowerPoint
Fig. 7.  Hole mobility versus the effective electric field under different interface charge areal densities.

DownLoad: Full-Size Img PowerPoint
Fig. 8.  Hole mobility versus the effective electric field for different thicknesses of Ge film.

DownLoad: Full-Size Img PowerPoint
Fig. 9.  Hole mobility versus thickness of Ge film for different inversion charge densities under the weak fields.

DownLoad: Full-Size Img PowerPoint

Table 1.   A part of the physical parameters used in simulation.

DownLoad: CSV
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]
[26]
[27]
[28]
[29]
[30]
[31]
[32]

    • Search

    Advanced Search >>

    GET CITATION

    shu

    Export: BibTex EndNote

    Article Metrics

    Article views: 3109 Times PDF downloads: 38 Times Cited by: 0 Times

    History

    Received: 30 July 2015 Revised: Online: Published: 01 April 2016

    Catalog

      Email This Article

      User name:
      Email:*请输入正确邮箱
      Code:*验证码错误
      Send
      Article Navigation >  Journal of Semiconductors  > 2016  >  37(4): 044004
      Wenyu Yuan, Jingping Xu, Lu Liu, Yong Huang, Zhixiang Cheng. A physical model of hole mobility for germanium-on-insulator pMOSFETs[J]. Journal of Semiconductors, 2016, 37(4): 044004. doi: 10.1088/1674-4926/37/4/044004 ****W Y Yuan, J P Xu, L Liu, Y Huang, Z X Cheng. A physical model of hole mobility for germanium-on-insulator pMOSFETs[J]. J. Semicond., 2016, 37(4): 044004. doi: 10.1088/1674-4926/37/4/044004.
      Citation:
      Wenyu Yuan, Jingping Xu, Lu Liu, Yong Huang, Zhixiang Cheng. A physical model of hole mobility for germanium-on-insulator pMOSFETs[J]. Journal of Semiconductors, 2016, 37(4): 044004. doi: 10.1088/1674-4926/37/4/044004 ****
      W Y Yuan, J P Xu, L Liu, Y Huang, Z X Cheng. A physical model of hole mobility for germanium-on-insulator pMOSFETs[J]. J. Semicond., 2016, 37(4): 044004. doi: 10.1088/1674-4926/37/4/044004.
      shu

      A physical model of hole mobility for germanium-on-insulator pMOSFETs

      DOI: 10.1088/1674-4926/37/4/044004

      • School of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan 430074, China

      Funds:

      Project supported by the National Natural Science Foundation of China (Nos. 61274112, 61176100, 61404055).

      More Information
      • Corresponding author: Email:jpxu@hust.edu.cn
      • Received Date: 2015-07-30
      • Accepted Date: 2015-10-14
      • Published Date: 2016-01-25

      Catalog

        Journal of Semiconductors © 2017 All Rights Reserved   京ICP备05085259号-2

        /

        DownLoad:  Full-Size Img  PowerPoint
        Return
        Return