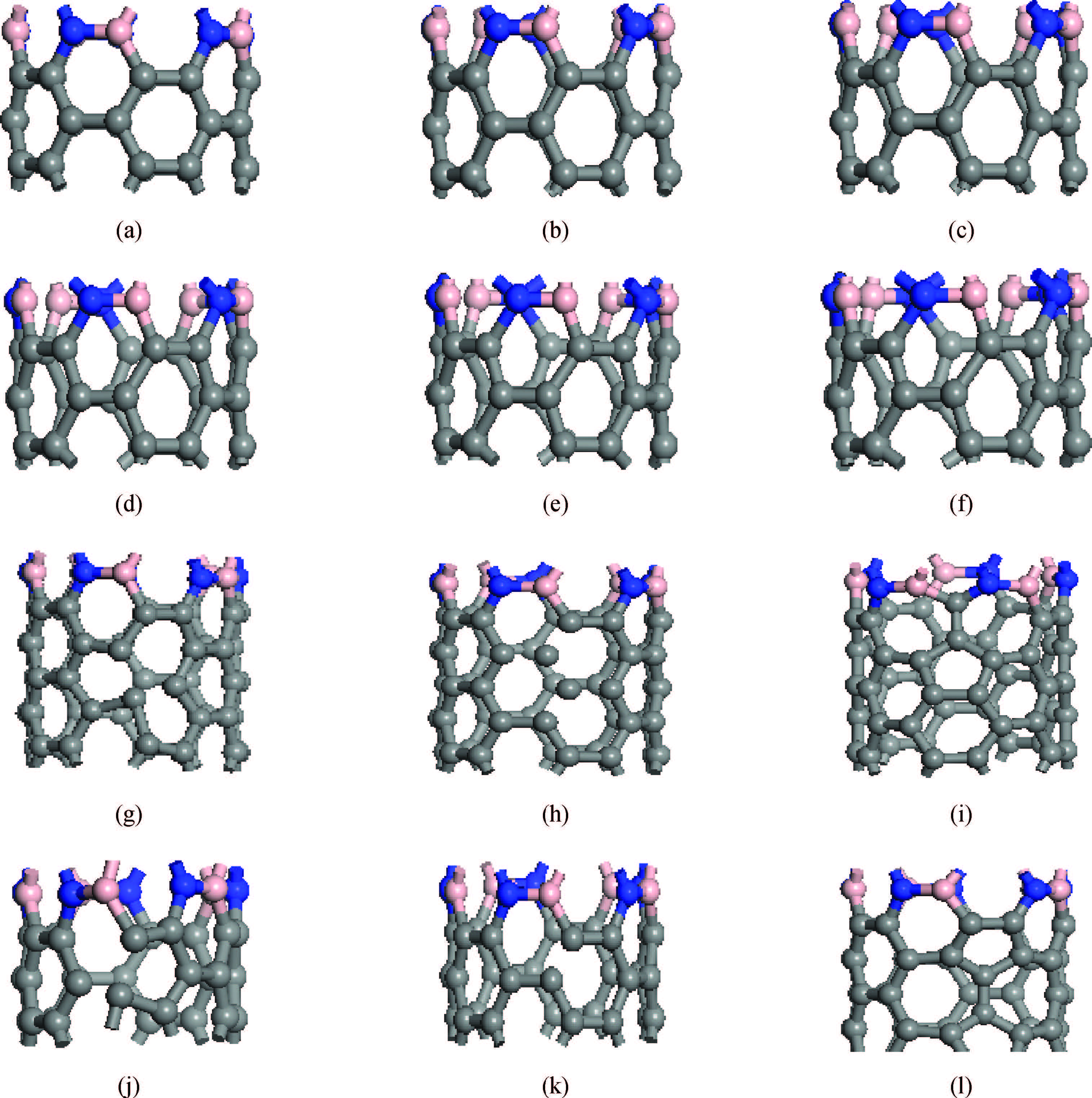
(a)-(f) The model with tension-twisting deformation,in which the twisting angles are 0°,3°,6°,9°,12° and 15°; and tension deformations is 5%. (g)-(i) The model with atomic,bond,STW defects. (j)-(l) The model with the combination of tension-twisting deformation (stretch of 5% and twist of 15%) and atomic,bond and STW defects.
| Citation: |
Guili Liu, Yan Jiang, Yuanyuan Song, Shuang Zhou, Tianshuang Wang. Influence of tension-twisting deformations and defects on optical and electrical properties of B, N doped carbon nanotube superlattices[J]. Journal of Semiconductors, 2016, 37(6): 063004. doi: 10.1088/1674-4926/37/6/063004
****
G L Liu, Y Jiang, Y Y Song, S Zhou, T S Wang. Influence of tension-twisting deformations and defects on optical and electrical properties of B, N doped carbon nanotube superlattices[J]. J. Semicond., 2016, 37(6): 063004. doi: 10.1088/1674-4926/37/6/063004.
|
Influence of tension-twisting deformations and defects on optical and electrical properties of B, N doped carbon nanotube superlattices
DOI: 10.1088/1674-4926/37/6/063004
More Information
-
Abstract
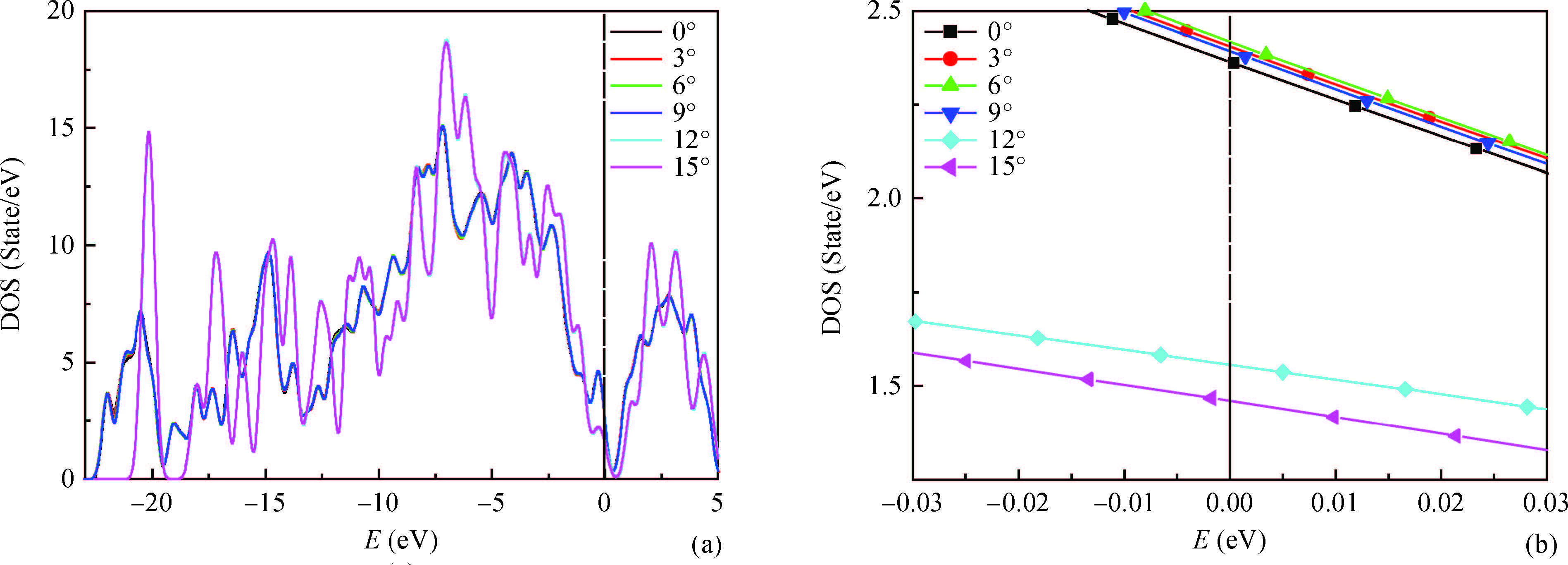
As the era of nanoelectronics is dawning, CNT (carbon nanotube), a one-dimensional nano material with outstanding properties and performances, has aroused wide attention. In order to study its optical and electrical properties, this paper has researched the influence of tension-twisting deformation, defects, and mixed type on the electronic structure and optical properties of the armchair carbon nanotube superlattices doped cyclic alternately with B and N by using the first-principle method. Our findings show that if tension-twisting deformation is conducted, then the geometric structure, bond length, binding energy, band gap and optical properties of B, N doped carbon nanotube superlattices with defects and mixed type will be influenced. As the degree of exerted tension-twisting deformation increases, B, N doped carbon nanotube superlattices become less stable, and B, N doped carbon nanotube superlattices with defects are more stable than that with exerted tension-twisting deformations. Proper tension-twisting deformation can adjust the energy gap of the system; defects can only reduce the energy gap, enhancing the system metallicity; while the mixed type of 5% tension, twisting angle of 15° and atomic defects will significantly increase the energy gap of the system. From the perspective of optical properties, doped carbon nanotubes may transform the system from metallicity into semi-conductivity. -
References
[1] Faria B, Silvestre N, Canongia Lopes J N. Induced anisotropy of chiral carbon nanotubes under combined tension-twisting. Mechanics of Materials, 2013, 58:97[2] Tada K, Yasuda M, Mitsueda T, et al. Molecular dynamics study of electron irradiation effects on mechanical properties of carbon nanotubes. Microelectron Eng, 2013, 107:50[3] Jeong B W, Lim J K, Sinnott S B. Torsional stiffening of carbon nanotube systems. Appl Phys Lett, 2007, 90:023102[4] Wu M H, Li X, Pan D, et al. Synthesis of nitrogen-doped single-walled carbon nanotubes and monitoring of doping by Raman spectroscopy. Chin Phys B, 2013, 22:086101[5] Karimov Kh S, Sulaiman K, Ahmad Z, et al. Novel pressure and displacement sensors based on carbon nanotubes. Chin Phys B, 2015, 24:018801[6] Zhang G X, Wang H H, Chen Y F, et al. Numerical simulations on effcet of Stone-Wales defects on mechanical properties of SWCNTs under axial stretch or twist loads. Journal of East China University of Science and Technology (Natural Science Edition), 2013, 01:8(in Chinese)[7] Zhang X W, Zhang K W. Use the molecular kynamics simulate the stability of single-walled carbon nanotube with vacancy defects. Journal of Jiangnan University (Natural Science Edition), 2011, 02:249(in Chinese)[8] Sharma A, Chandra R, Kumar P, et al. Effect of Stone-Wales and vacancy defects on elastic moduli of carbon nanotubes and their composites using molecular dynamics simulation. Computational Materials Science, 2014, 86:01[9] Partovi-Azar P, Jand S P, Namiranian A, et al. Electronic features induced by Stone-Wales defects in zigzag and chiral carbon nanotubes. Computational Materials Science, 2013, 79:82[10] Qing X Z, Chao Y W, Zhi B F, et al. Effects of various defects on the electronic properties of single-walled carbon nanotubes:a first principle study. Frontiers of Physics, 2014, 09:200[11] Xie Y, Luo Y, Liu S J. The effects of the uniaxial pressure on electronic structures of the (6,6) single-walled carbon nanotube crysta. Acta Physica Sinica, 2008, 57:4364(in Chinese)[12] Jin L, Fu H G, Xie Y, et al, Field emission properties of capped carbon nanotubes doped by alkali metals:a theoretical investigation. Chin Phys B, 2012, 05:651[13] Yu Z Q, Zhang C H, Li S D, et al. Electronic structures and optoelectronic properties of C/Ge-doped silicon nanotubes. Journal of Inorganic Materials, 2015, 03:233(in Chinese)[14] Marlo M, Milman V. Density-functional study of bulk and surface properties of titanium nitride using different exchange-correlation functionals. Phys Rev B, 2000, 62:2899[15] Jiang Y, Liu G L. Infuences of shear deformation on electronic structure and optical properties of B, N doped carbon nanotube superlattices. Acta Physica Sinica, 2015, 64(14):1(in Chinese) -
Proportional views





 DownLoad:
DownLoad: