| Citation: |
Caixia Guo, Congxin Xia, Tianxing Wang, Yufang Liu. Carbon-doping-induced negative differential resistance in armchair phosphorene nanoribbons[J]. Journal of Semiconductors, 2017, 38(3): 033005. doi: 10.1088/1674-4926/38/3/033005
****
C X Guo, C X Xia, T X Wang, Y F Liu. Carbon-doping-induced negative differential resistance in armchair phosphorene nanoribbons[J]. J. Semicond., 2017, 38(3): 033005. doi: 10.1088/1674-4926/38/3/033005.
|
Carbon-doping-induced negative differential resistance in armchair phosphorene nanoribbons
DOI: 10.1088/1674-4926/38/3/033005
More Information
-
Abstract
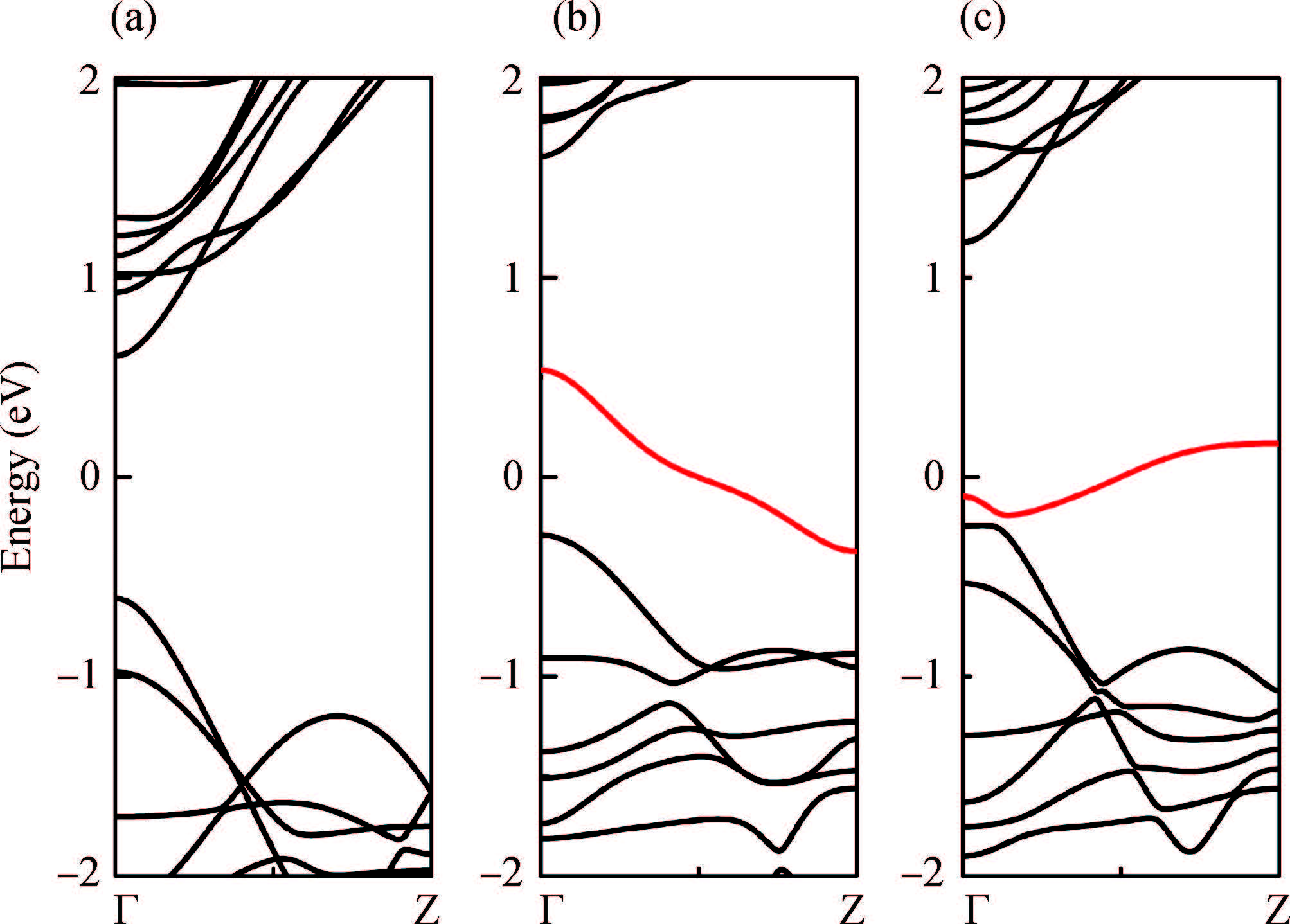
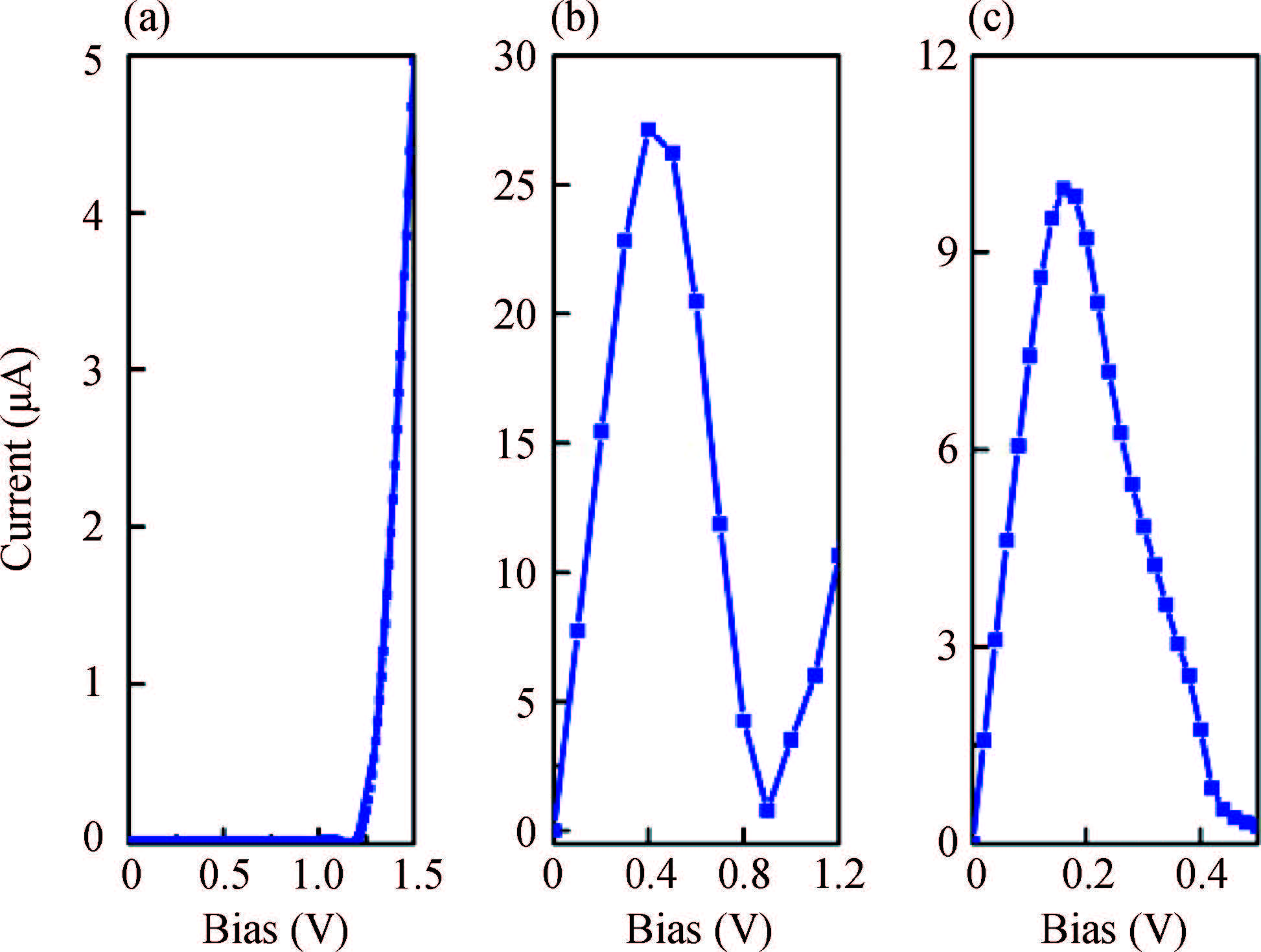
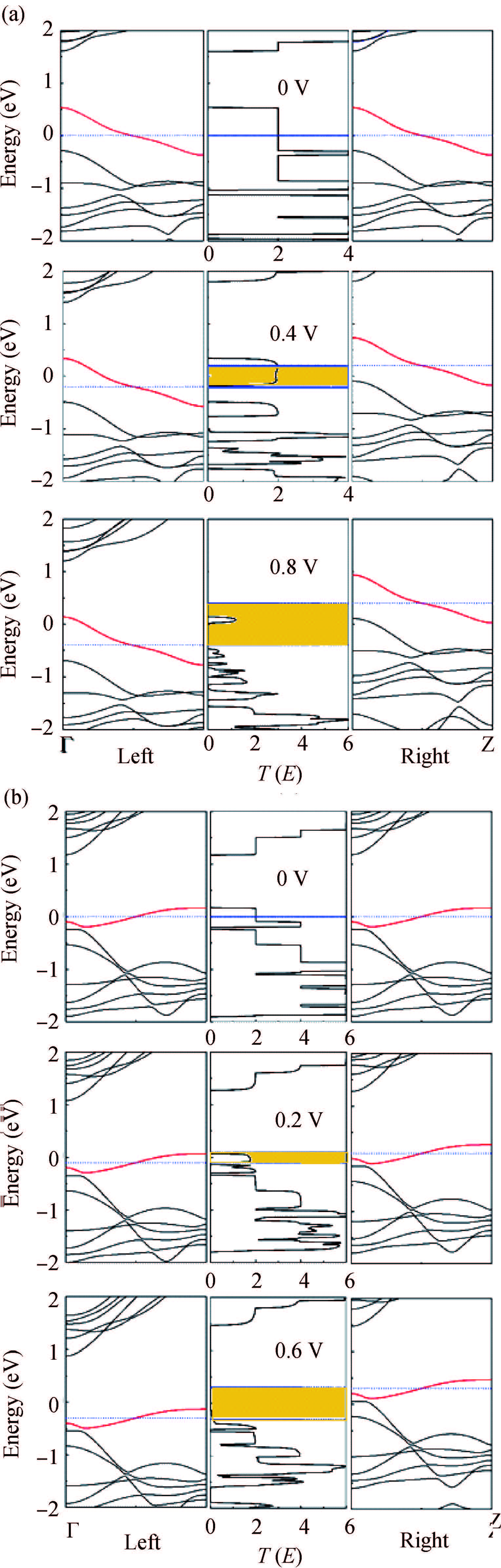
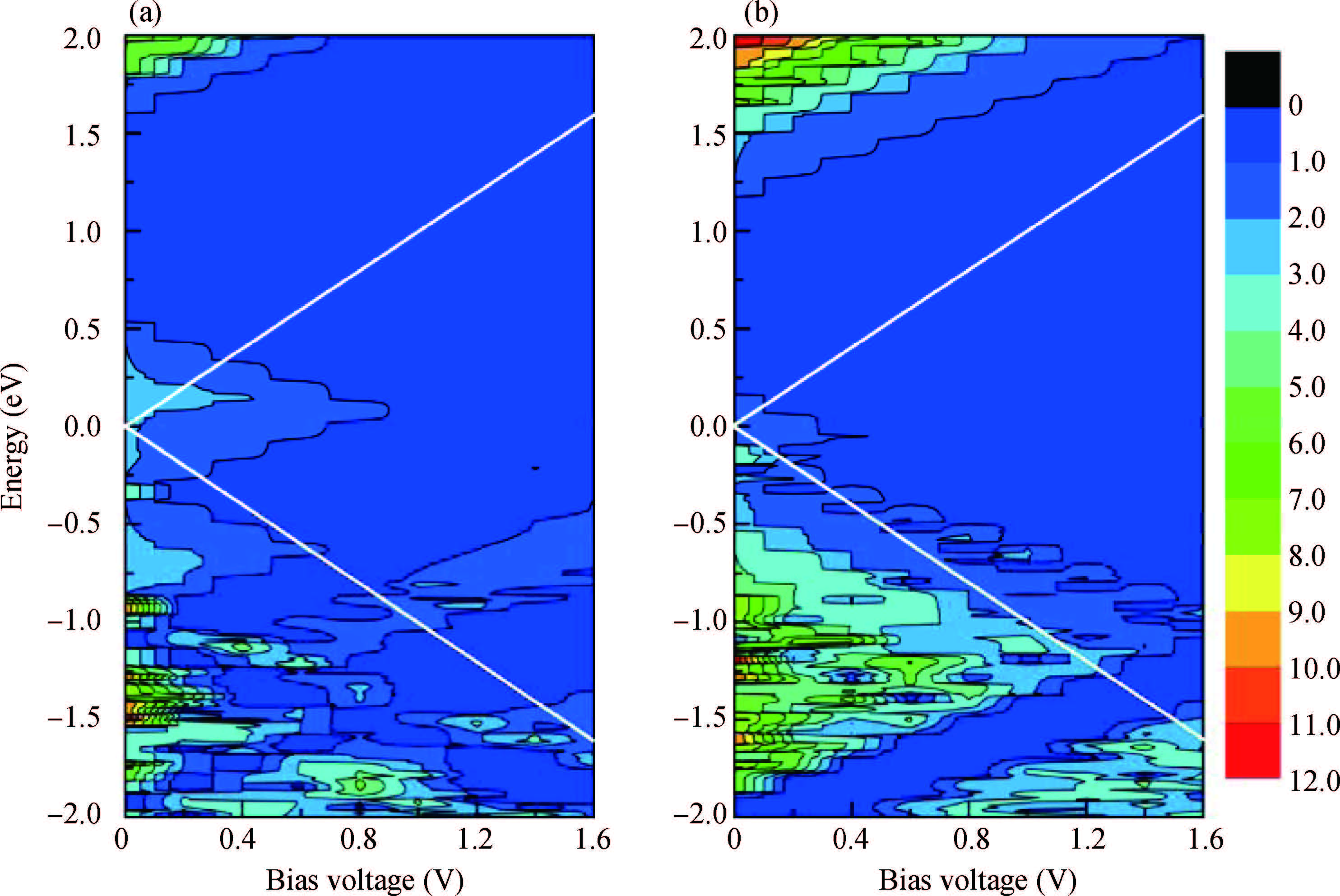
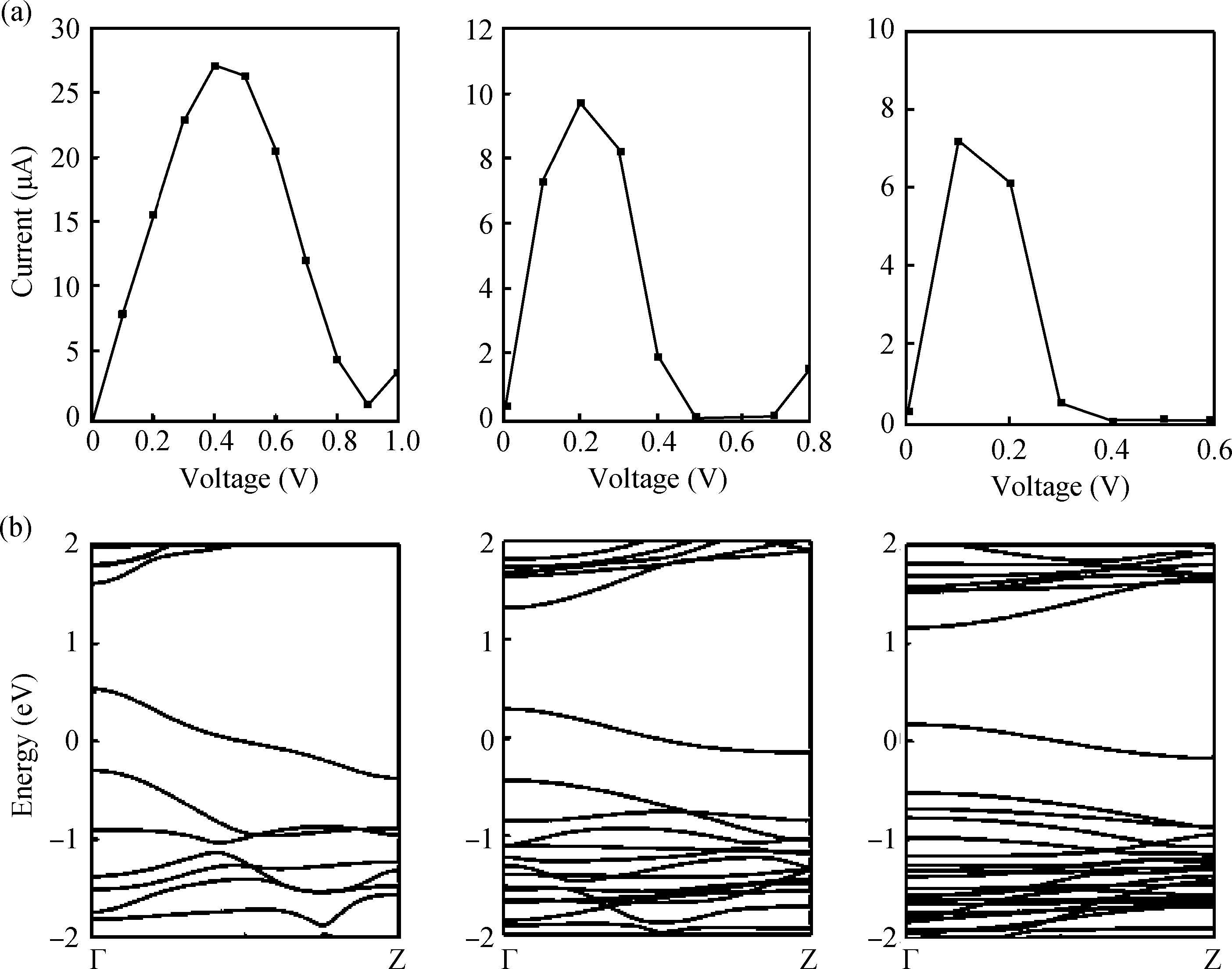
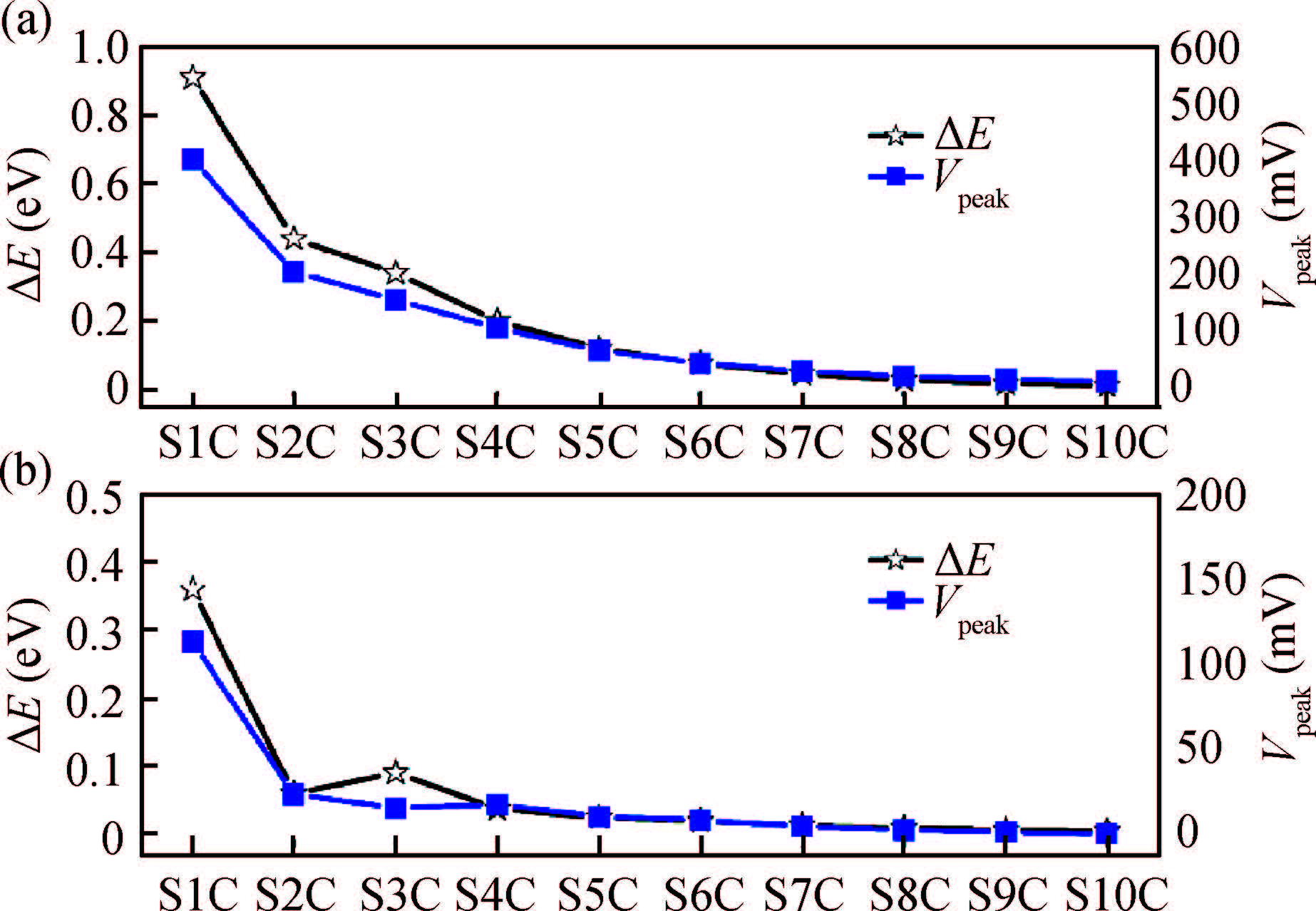
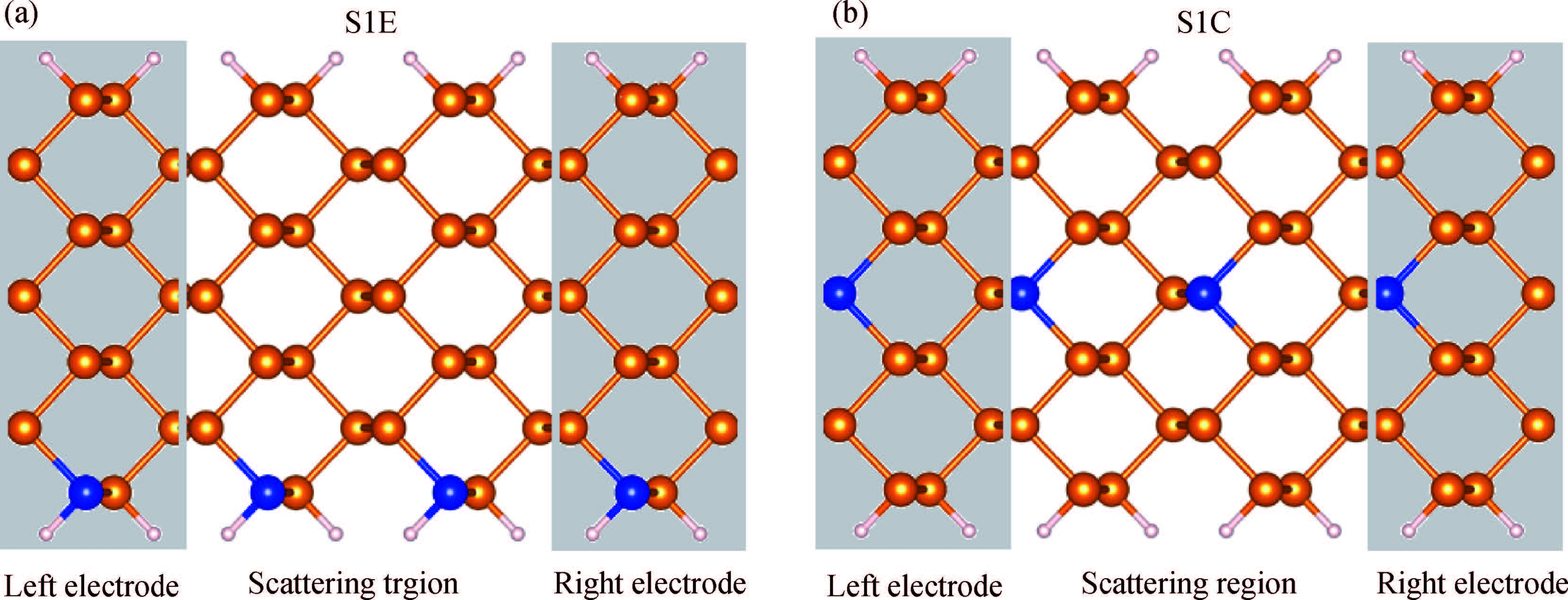
By using a combined method of density functional theory and non-equilibrium Green's function formalism, we investigate the electronic transport properties of carbon-doped armchair phosphorene nanoribbons (APNRs). The results show that C atom doping can strongly affect the electronic transport properties of the APNR and change it from semiconductor to metal. Meanwhile, obvious negative differential resistance (NDR) behaviors are obtained by tuning the doping position and concentration. In particular, with reducing doping concentration, NDR peak position can enter into mV bias range. These results provide a theoretical support to design the related nanodevice by tuning the doping position and concentration in the APNRs. -
References
[1] Li K, Yu Y, Guo J, et al. Black phosphorus field-effect transistors. Nat Nanotechnol, 2014, 9(5):372 doi: 10.1038/nnano.2014.35[2] Nathaniel G, Darshana W, Shi Y, et al. Gate tunable quantum oscillations in air-stable and high mobility few-layer phosphorene heterostructures. 2D Mater, 2015, 2:011001 https://www.researchgate.net/publication/269116255_Gate_Tunable_Quantum_Oscillations_in_Air-Stable_and_High_Mobility_Few-Layer_Phosphorene_Heterostructures[3] Qiao J, Kong X H, Hu Z X, et al. High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus. Nat Commun, 2014, 5:4475 http://www.doc88.com/p-7078266727511.html[4] Zhang C, Xiang G, Lan M, et al. Homostructured negative differential resistance device based on zigzag phosphorene nanoribbons. RSC Adv, 2015, 5(50):40358 doi: 10.1039/C5RA04056F[5] Brown E R, Söderström J R, Parker C D, et al. Oscillations up to 712 GHz in InAs/AlSb resonant-tunneling diodes. Appl Phys Lett, 1991, 58(20):2291 doi: 10.1063/1.104902[6] Broekaert T P, Brar B, Van der Wagt J P A, et al. A monolithic 4- bit 2-Gsps resonant tunneling analog-to-digital converter. IEEE J Solid-State Circuits, 1998, 33(9):1342 doi: 10.1109/4.711333[7] Büttiker M, Imry Y, Landauer R, et al. Generalized many-channel conductance formula with application to small rings. Phys Rev B, 1985, 31(10):6207 doi: 10.1103/PhysRevB.31.6207[8] Rommel S L, Dillon T E, Berger P R, et al. Si-based interband tunneling devices for high-speed logic and low power memory applications. International Electron Devices Meeting, 1998:1035 http://www.academia.edu/15052314/Si-based_interband_tunneling_devices_for_high-speed_logic_and_low_power_memory_applications[9] An Y P, Wei X, Yang Z. Improving electronic transport of zigzag graphene nanoribbons by ordered doping of B or N atoms. Phys Chem Chem Phys, 2012, 14(45):15802 doi: 10.1039/c2cp42123b[10] Liu N, Liu J B, Gao G Y, et al. Carbon doping induced giant low bias negative differential resistance in boron nitride nanoribbon. Phys Lett A, 2014, 378(30/31):2217 https://www.researchgate.net/publication/263202268_Carbon_doping_induced_giant_low_bias_negative_differential_resistance_in_boron_nitride_nanoribbon[11] Pramanik A, Sarkar S, Sarkar P. Doped GNR p-n junction as high performance NDR and rectifying device. J Phys Chem C, 2012, 116(34):18064 doi: 10.1021/jp304582k[12] Hao R, Li Q, Luo Y, et al. Graphene nanoribbon as a negative differential resistance device. Appl Phys Lett, 2009, 94(17):173110 doi: 10.1063/1.3126451[13] Zhao P, Liu D S, Li S J, et al. Giant low bias negative differential resistance induced by nitrogen doping in graphene nanoribbon. Chem Phys Lett, 2012, 554:172 doi: 10.1016/j.cplett.2012.10.045[14] Zhao P, Liu D S, Liu H Y, et al. Low bias negative differential resistance in C60 dimer modulated by gate voltage. Organ Electron, 2013, 14(4):1109 doi: 10.1016/j.orgel.2013.01.034[15] Min Y, Yao K L, Fu H H, et al. First-principles study of strong rectification and negative differential resistance induced by charge distribution in single molecule. J Chem Phys, 2010, 132(21):214703 doi: 10.1063/1.3447380[16] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett, 1996, 77(18):3865 doi: 10.1103/PhysRevLett.77.3865[17] Yu W, Zhu Z, Niu C Y, et al. Anomalous doping effect in black phosphorene using first-principles calculations. Phys Chem Chem Phys, 2015, 17(25):16351 doi: 10.1039/C5CP01732G[18] Li W, Zhang G, Zhang Y W. Electronic properties of edgehydrogenated phosphorene nanoribbons:a first-principles study. J Phys Chem C, 2014, 118(38):22368 doi: 10.1021/jp506996a[19] Fei R, Yang L. Strain-engineering the anisotropic electrical conductance of few-layer black phosphorus. Nano Lett, 2014, 14(5):2884 doi: 10.1021/nl500935z[20] Guo C X, Xia C X, Fang L Z, et al. Tuning anisotropic electronic transport properties of phosphorene via substitutional doping. Phys Chem Chem Phys, 2016, 18:25869 doi: 10.1039/C6CP04508A[21] Wu Y, Wang Y, Wang J, et al. Electrical transport across metal=two-dimensional carbon junctions:edge versus side contacts. AIP Adv, 2012, 2(1):012132 doi: 10.1063/1.3684617 -
Proportional views





 DownLoad:
DownLoad: