| Citation: |
M. Koizumi, J. Goto, S. Matsuki. Dynamic nuclear self-polarization of III–V semiconductors[J]. Journal of Semiconductors, 2018, 39(8): 082001. doi: 10.1088/1674-4926/39/8/082001
****
M. Koizumi, J. Goto, S. Matsuki, Dynamic nuclear self-polarization of III–V semiconductors[J]. J. Semicond., 2018, 39(8): 082001. doi: 10.1088/1674-4926/39/8/082001.
|
Dynamic nuclear self-polarization of III–V semiconductors
DOI: 10.1088/1674-4926/39/8/082001
More Information
-
Abstract
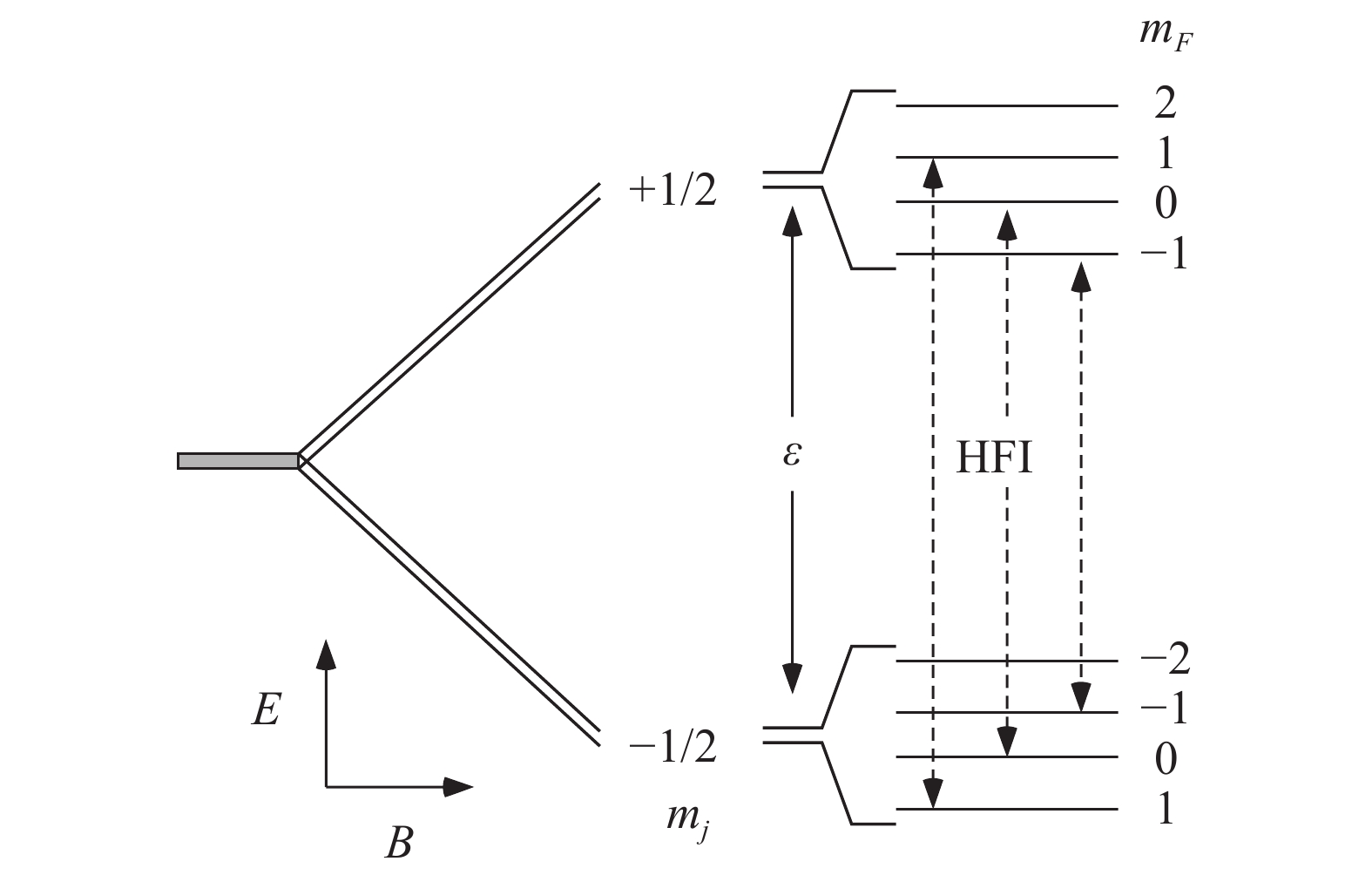
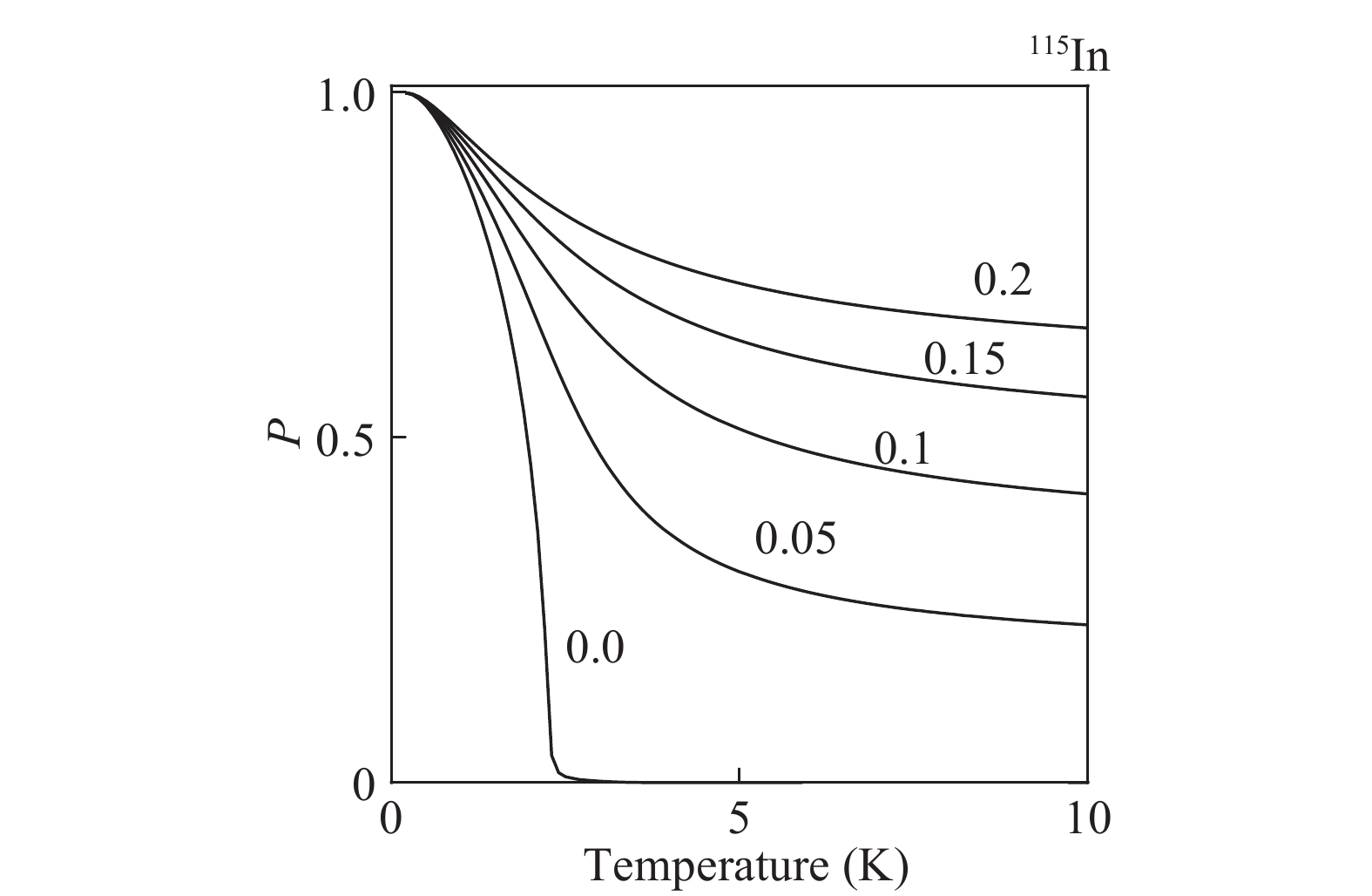
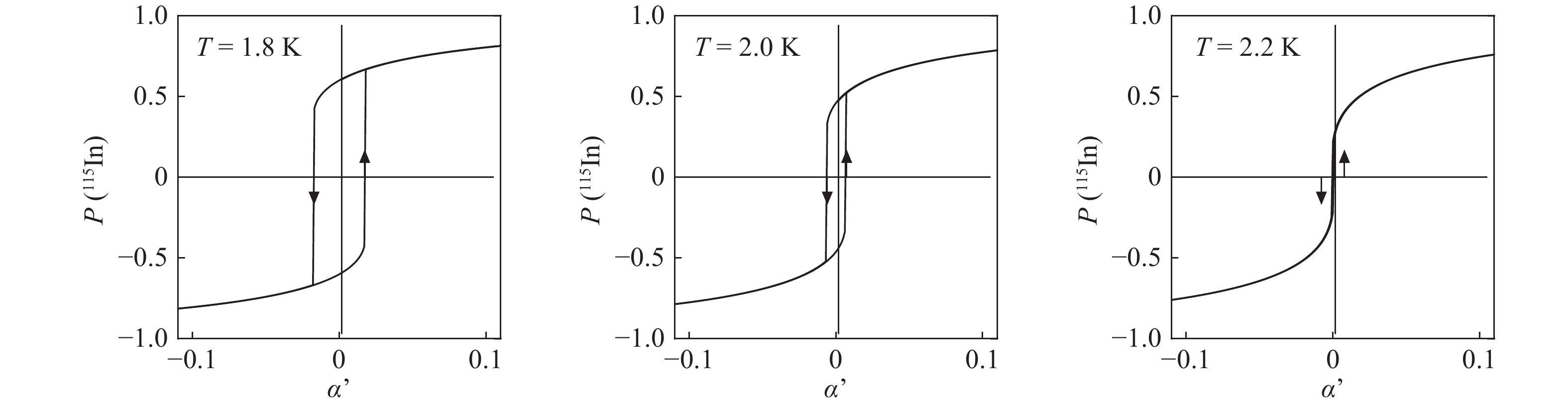
III–V semiconductors exhibit dynamic nuclear self-polarization (DYNASP) owing to the contact hyperfine interaction (HFI) between optically excited conduction electrons and lattice nuclei. In the self-polarization process at a low temperature, electron spin state and the nuclear polarization (magnetization) exchange a positive feedback, increasing energy splitting of the conduction electron states, thereby a large nuclear polarization. This phenomenon was theoretically predicted previously for conduction electrons excited linearly and elliptically polarized light. The polarization of the conduction electrons was represented by a parameterα in a formula for nuclear polarization (Eq. (9) in Ref. [1]); however, the effect of external magnetic fields on the nuclear polarization was not considered. Therefore, this study introduces this effect by further extending the previous studies. Herein, α′ represents the combination of the effects of elliptically polarized electrons and an external magnetic field, which is used in the equations presented in previous studies. When α′ = 0, a large nuclear polarization is obtained below critical temperature Tc, but no polarization occurs above Tc. When α′ > 0, the nuclear polarization is enhanced above Tc. Below Tc, the nuclear polarization follows a hysteresis curve when α′ is partially manipulated by adjusting the degree of the polarization of the exciting laser.-
Keywords:
- nuclear polarization,
- optical polarization,
- InP,
- overhauser,
- III–V semiconductor
-
References
[1] Koizumi M, Goto J, Matsuki S. Dynamic nuclear self-polarization with circularly polarized light. J Appl Phys, 2011, 110: 013911 doi: 10.1063/1.3602118[2] Sealy B J. Review of III–V semiconductor materials and devices. J Institution of Electron Radio Eng, 1987, 57: S2 doi: 10.1049/jiere.1987.0012[3] Mokkapati S, Jagadish C. III–V compound SC for optoelectronic devices. Mater Today, 2009, 12: 22 doi: 10.1016/S1369-7021(09)70110-5[4] Tanabe K. A review of ultrahigh efficiency III–V semiconductor compound solar cells: multijunction tandem, lower dimensional, photonic up/down conversion and plasmonic nanometallic structures. Energies, 2009, 2: 504 doi: 10.3390/en20300504[5] Dasgupta N P, Sun J, Liu C, et al. Transparent electrodes: highly conductive PEDOT:PSS nanofibrils induced by solution‐processed crystallization. Adv Mater, 2014, 26: 2137 doi: 10.1002/adma.v26.14[6] Tamirat Y. The role of nanotechnology in semiconductor industry. J Mater Sci Nanotechnol, 2017, 5: 202[7] Liu Y, Liang B, Guo Q, et al. Electronic coupling in nanoscale InAs/GaAs quantum dot pairs separated by a thin Ga(Al)As spacer. Nanoscale Res Lett, 2015, 10: 271 doi: 10.1186/s11671-015-0973-5[8] Frolov S M, Plissard S R, Nadj-Perge S, et al. Quantum computing based on semiconductor nanowires. Mater Res Soc, 2013, 38: 809 doi: 10.1557/mrs.2013.205[9] Ohno H. Quantum computing based on semiconductor nanowires. J Magn Magn Mater, 1999, 200: 110 doi: 10.1016/S0304-8853(99)00444-8[10] Jungwirth T, Sinova J, Maček J, et al. Theory of ferromagnetic (III,Mn)V semiconductors. Rev Mod Phys, 2006, 78: 809 doi: 10.1103/RevModPhys.78.809[11] Chen Y, Kim J, Puls J, et al. Current‐induced control of the electron–nuclear spin system in semiconductors on a micrometer scale. Phys Status Solidi B, 2014, 251: 1777 doi: 10.1002/pssb.201350255[12] Dyakonov M I, Perel V I. Dynamic self-polarization of nuclei in solids. JETP Lett, 1972, 16: 398[13] Dyakonov M I. Optical recording of dynamic self-polarization of nuclei in semiconductors. Sov Phys JETP, 1975, 40: 746[14] Dyakonov M I, Perel V I. Optical orientation. Edited by F Meier, B. Zakharchenya. North-Holand, 1984: 11[15] Koizumi M, Goto J, Matsuki S, et al. Dynamic nuclear self-polarization for measurements of nuclear magnetic moments. Nucl Instr Meth Phys Res B, 2013, 317: 689 doi: 10.1016/j.nimb.2013.07.042[16] Overhauser A W. Polarization of nuclei in metals. Phys Rev, 1953, 92: 411 doi: 10.1103/PhysRev.92.411[17] Paget D, Lampel G, Sapoval B, et al. Low field electron-nuclear spin coupling in gallium arsenide under optical pumping conditions. Phys Rev B, 1977, 15: 5780 doi: 10.1103/PhysRevB.15.5780[18] Gotschy B, Denninger G, Obloh H, et al. Overhauser shift and dynamic nuclear polarization in InP. Solid State Commun, 1989, 71: 629 doi: 10.1016/0038-1098(89)90551-6[19] Clerjaud B, Gendron F, Obloh H, et al. Effect of nuclear polarization on the conduction-electron spin resonance in InP. Phys Rev B, 1989, 40: 2042[20] Raghavan P. Table of nuclear moments. Atomic Data and Nuclear Data Tables, 1989, 42: 189 doi: 10.1016/0092-640X(89)90008-9[21] Michal C A, Tycko R. Stray-field NMR imaging and wavelength dependence of optically pumped nuclear spin polarization in InP. Phys Rev B, 1999, 60: 8672 doi: 10.1103/PhysRevB.60.8672[22] Goto A, Hashi K, Shimizu T, et al. Efficiency of the optical pumping qubit initializer for solid-state NMR quantum computers. J Magn Magn Mater, 2004, 272-276: E1669 doi: 10.1016/j.jmmm.2003.12.958[23] Rikovska J, Giles T, Stone N J, et al. First on-line beta-NMR on oriented nuclei: magnetic dipole moments of the (νp1/2)−1 1/2− ground state in N67i and (πp3/2)+1 3/2− ground state in C69u. Phys Rev Lett, 2000, 85: 1392 doi: 10.1103/PhysRevLett.85.1392[24] Nagae D, Ueno H, Kameda D, et al. Ground-state electric quadrupole moment of Al31. Phys Rev C, 2009, 79: 027301 doi: 10.1103/PhysRevC.79.027301 -
Proportional views





 DownLoad:
DownLoad: