| Citation: |
Yilun Gu, Shengli Guo, Fanlong Ning. Progress on microscopic properties of diluted magnetic semiconductors by NMR and μSR[J]. Journal of Semiconductors, 2019, 40(8): 081506. doi: 10.1088/1674-4926/40/8/081506
****
Y L Gu, S L Guo, F L Ning, Progress on microscopic properties of diluted magnetic semiconductors by NMR and μSR[J]. J. Semicond., 2019, 40(8): 081506. doi: 10.1088/1674-4926/40/8/081506.
|
Progress on microscopic properties of diluted magnetic semiconductors by NMR and μSR
DOI: 10.1088/1674-4926/40/8/081506
More Information
-
Abstract
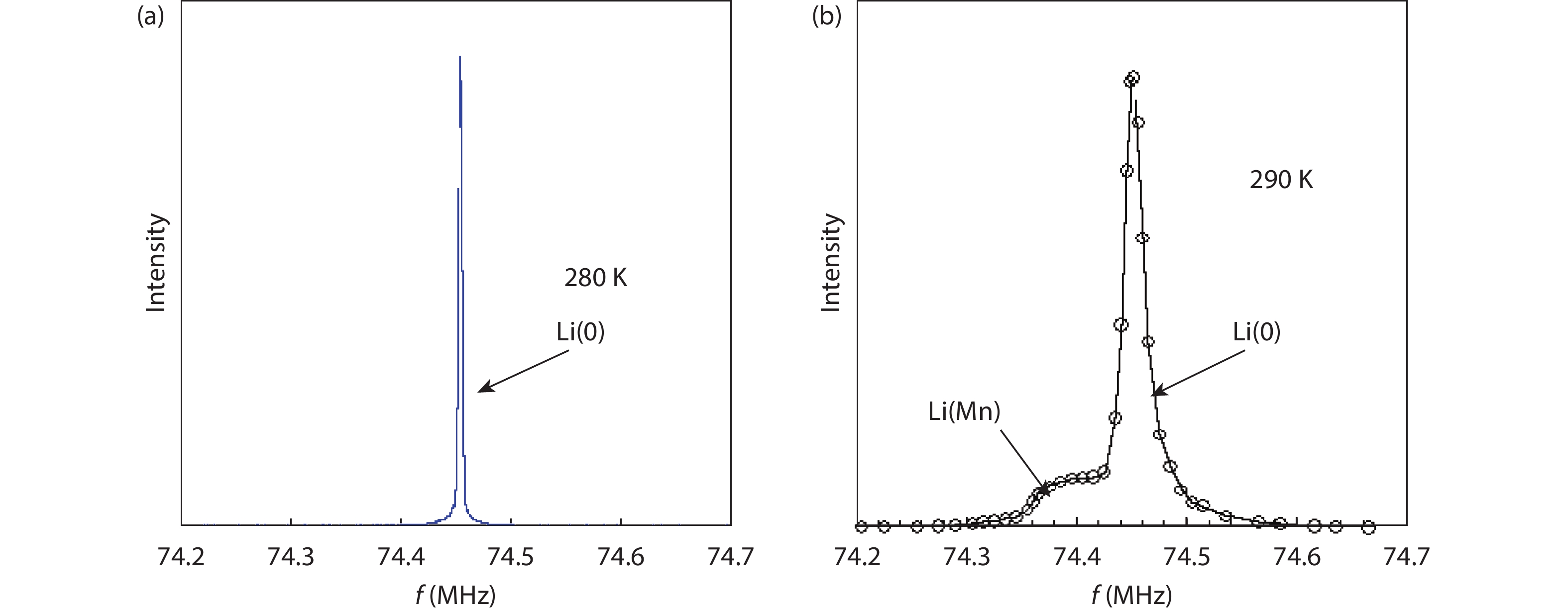
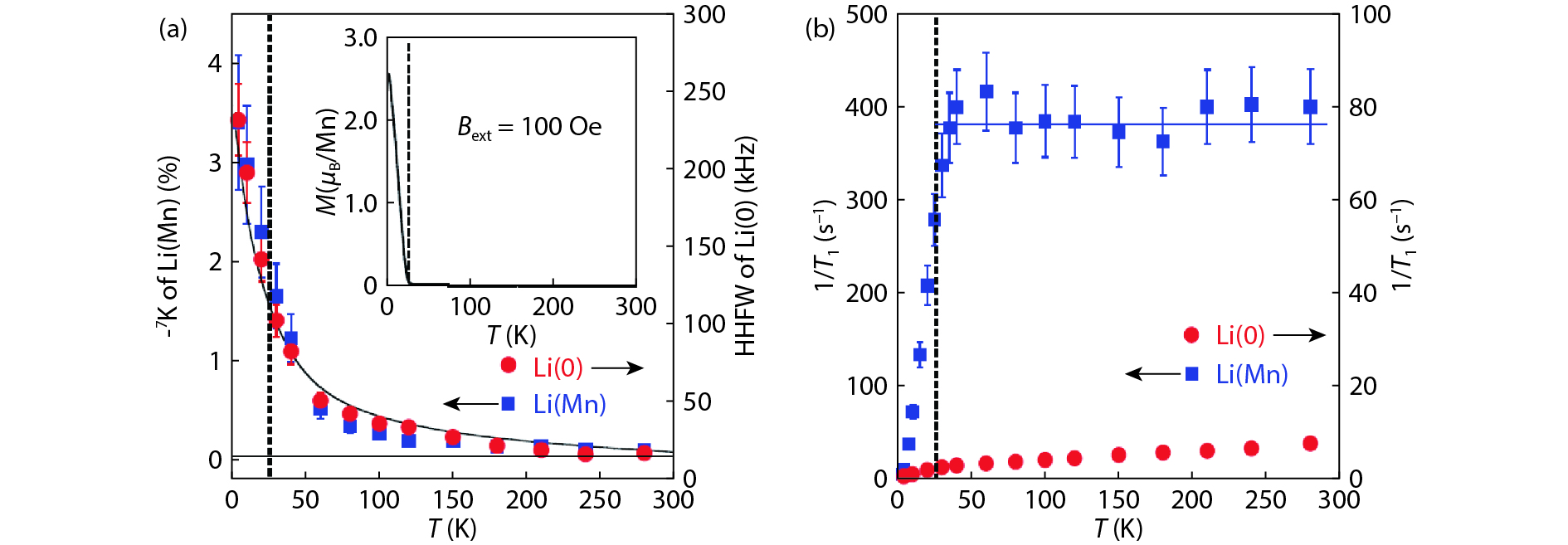
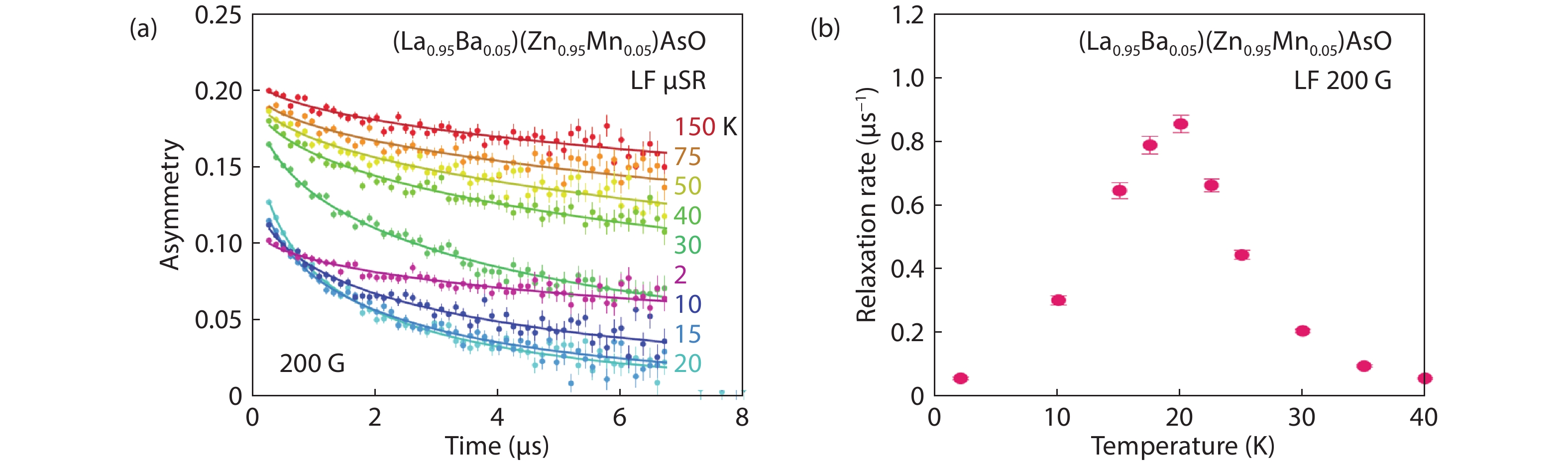
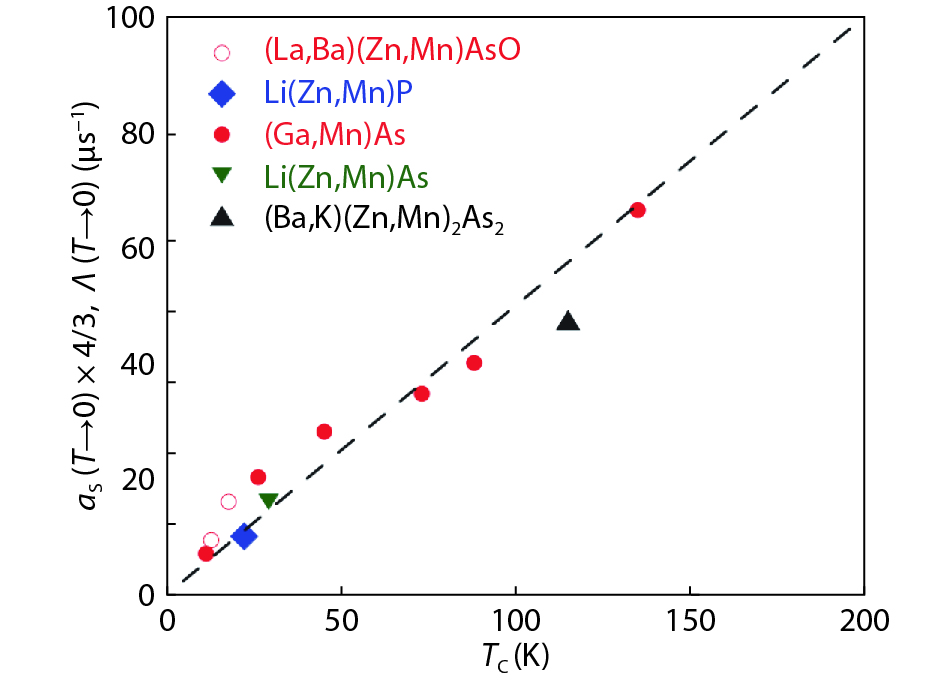
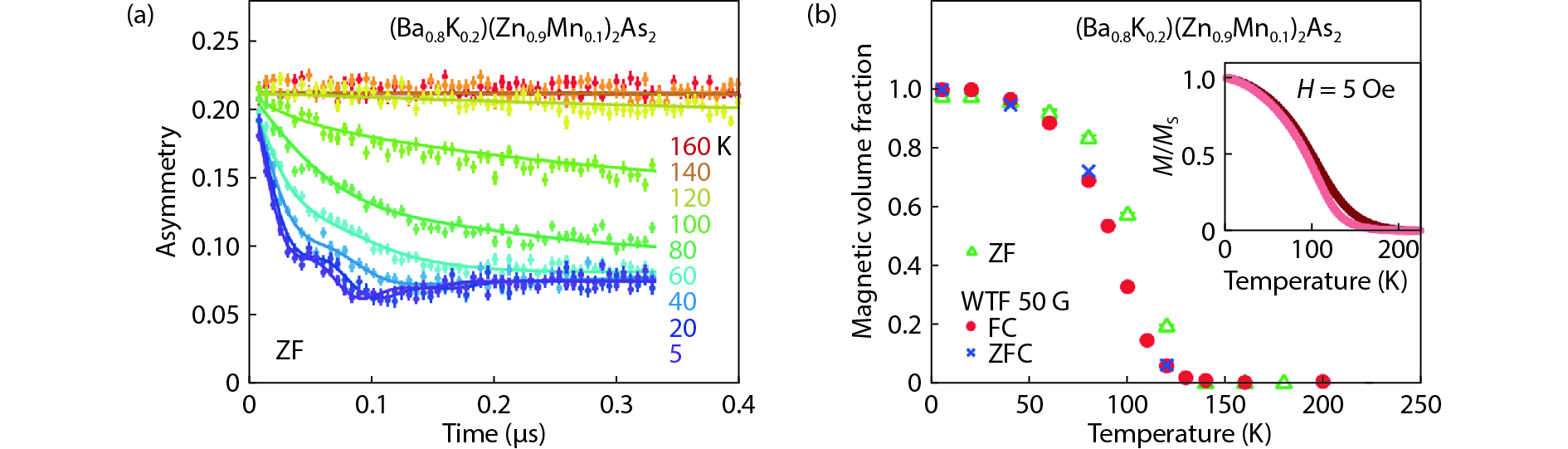
Diluted magnetic semiconductors (DMSs) that possess both properties of semiconductors and ferromagnetism, have attracted a lot of attentions due to its potential applications for spin-sensitive electronic devices. Recently, a series of bulk form DMSs isostructural to iron-based superconductors have been reported, which can be readily investigated by microscopic experimental techniques such as nuclear magnetic resonance (NMR) and muon spin rotation (μSR). The measurements have demonstrated that homogeneous ferromagnetism is achieved in these DMSs. In this review article, we summarize experimental evidences from both NMR and μSR measurements. NMR results have shown that carriers facilitate the interactions between distant Mn atoms, while μSR results indicate that these bulk form DMSs and (Ga,Mn)As share a common mechanism for the ferromagnetic exchange interactions. -
References
[1] Von Molnar S, Read D. New materials for semiconductor spin-electronics. Proc IEEE, 2003, 91(5), 715 doi: 10.1109/JPROC.2003.811803[2] Matthias B T, Bozorth R M, Van Vleck J H. Ferromagnetic interaction in EuO. Phys Rev Lett, 1961, 7(5), 160 doi: 10.1103/PhysRevLett.7.160[3] Menyuk N, Dwight K, Arnott R J, et al. Ferromagnetism in CdCr2Se4 and CdCr2S4. J Appl Phys, 1966, 37(3), 1387 doi: 10.1063/1.1708484[4] Twardowski A, Swagten H J M, de Jonge W J M, et al. Magnetic behavior of the diluted magnetic semiconductor Zn1– xMnxSe. Phys Rev B, 1987, 36(13), 7013 doi: 10.1103/PhysRevB.36.7013[5] Ferrand D, Cibert J, Wasiela A, et al. Carrier-induced ferromagnetism in p-Zn1– xMn xTe. Phys Rev B, 2001, 63(8), 085201 doi: 10.1103/PhysRevB.63.085201[6] Aggarwal R L, Jasperson S N, Stankiewicz J, et al. Magnetoreflectance at the band edge in Cd1– xMnxSe. Phys Rev B, 1983, 28(12), 6907 doi: 10.1103/PhysRevB.28.6907[7] Haury A, Wasiela A, Arnoult A, et al. Observation of a ferromagnetic transition induced by two-dimensional hole gas in modulation-doped CdMnTe quantum wells. Phys Rev Lett, 1997, 79(3), 511 doi: 10.1103/PhysRevLett.79.511[8] Ohno H, Shen A, Matsukura F, et al. (Ga, Mn)As: A new diluted magnetic semiconductor based on GaAs. Appl Phys Lett, 1996, 69(3), 363 doi: 10.1063/1.118061[9] Ohno H. Making nonmagnetic semiconductors ferromagnetic. Science, 1998, 281(5379), 951 doi: 10.1126/science.281.5379.951[10] Jungwirth T, Sinova J, Mašek J, et al. Theory of ferromagnetic (III,Mn)V semiconductors. Rev Mod Phys, 2006, 78(3), 809 doi: 10.1103/RevModPhys.78.809[11] Dietl T. A ten-year perspective on dilute magnetic semiconductors and oxides. Nat Mater, 2010, 9(12), 965 doi: 10.1038/nmat2898[12] Wang M, Campion R P, Rushforth A W, et al. Achieving high curie temperature in (Ga, Mn)As. Appl Phys Lett, 2008, 93(13), 132103 doi: 10.1063/1.2992200[13] Chen L, Yan S, Xu P F, et al. Low-temperature magnetotransport behaviors of heavily Mn-doped (Ga, Mn)As films with high ferromagnetic transition temperature. Appl Phys Lett, 2009, 95(18), 182505 doi: 10.1063/1.3259821[14] Chen L, Yang X, Yang F, et al. Enhancing the Curie temperature of ferromagnetic semiconductor (Ga, Mn)As to 200 K via nanostructure engineering. Nano Lett, 2011, 11(7), 2584 doi: 10.1021/nl201187m[15] Tanaka M, Ohya S, Hai P N. Recent progress in III–V based ferromagnetic semiconductors: Band structure, Fermi level, and tunneling transport. Appl Phys Rev, 2014, 1(1), 011102 doi: 10.1063/1.4840136[16] Deng Z, Zhao K, Gu B, et al. Diluted ferromagnetic semiconductor Li(Zn, Mn)P with decoupled charge and spin doping. Phys Rev B, 2013, 88(8), 081203 doi: 10.1103/PhysRevB.88.081203[17] Deng Z, Jin C Q, Liu Q Q, et al. Li(Zn, Mn)As as a new generation ferromagnet based on a I–II–V semiconductor. Nat Commun, 2011, 2(1), 422 doi: 10.1038/ncomms1425[18] Ding C, Man H, Qin C, et al. (La1– xBax)(Zn1– xMnx)AsO: A two-dimensional 1111-type diluted magnetic semiconductor in bulk form. Phys Rev B, 2013, 88(4), 041102 doi: 10.1103/PhysRevB.88.041102[19] Zhao K, Deng Z, Wang X C, et al. New diluted ferromagnetic semiconductor with Curie temperature up to 180 K and isostructural to the ’122’ iron-based superconductors. Nat Commun, 2013, 4(1), 1442 doi: 10.1038/ncomms2447[20] Guo S, Man H, Wang K, et al. Ba(Zn, Co)2As2: A diluted ferromagnetic semiconductor with n-type carriers and isostructural to 122 iron-based superconductors. Phys Rev B, 2019, 99(15), 155201 doi: 10.1103/PhysRevB.99.155201[21] Zhao K, Chen B, Zhao G, et al. Ferromagnetism at 230 K in (Ba0:7K0:3)(Zn0:85Mn0:15)2As2 diluted magnetic semiconductor. Chin Scie Bull, 2014, 59(21), 2524 doi: 10.1007/s11434-014-0398-z[22] Guo S, Ning F L. Progress of novel diluted ferromagnetic semiconductors with decoupled spin and charge doping: Counterparts of fe-based superconductors. Chin Phys B, 2018, 27(9), 097502 doi: 10.1088/1674-1056/27/9/097502[23] Dunsiger S R, Carlo J P, Goko T, et al. Spatially homogeneous ferromagnetism of (Ga, Mn)As. Nat Mater, 2010, 9(4), 299 doi: 10.1038/nmat2715[24] Masek J, Kudrnovsk J, Mca F, et al. Dilute moment n-type ferromagnetic semiconductor Li(Zn, Mn)As. Phys Rev Lett, 2007, 98(6), 067202 doi: 10.1103/PhysRevLett.98.067202[25] Han W, Chen B J, Gu B, et al. Li(Cd, Mn)P: a new cadmium based diluted ferromagnetic semiconductor with independent spin & charge doping. Sci Rep, 2019, 9(1), 7490 doi: 10.1038/s41598-019-43754-x[26] Wang Q, Man H, Ding C, et al. Li1.1(Zn1– xCrx)As: Cr doped I–II–V diluted magnetic semiconductors in bulk form. J Appl Phys, 2014, 115(8), 083917 doi: 10.1063/1.4867299[27] Guo S L, Zhao Y, Man H Y, et al. μSR investigation of a new diluted magnetic semiconductor Li(Zn, Mn, Cu)As with Mn and Cu codoping at the same Zn sites. J Phys: Condens Matter, 2016, 28(36), 366001 doi: 10.1088/0953-8984/28/36/366001[28] Ding C, Qin C, Man H, et al. NMR investigation of the diluted magnetic semiconductor Li(Zn1– xMnx)P (x = 0. Phys Rev B, 2013, 88(4), 041108 doi: 10.1103/PhysRevB.88.041108[29] Ning F L, Man H, Gong X, et al. Suppression of TC by overdoped Li in the diluted ferromagnetic semiconductor Li1+ y(Zn1- xMnx)P: A μSR investigation. Phys Rev B, 2014, 90(8), 085123 doi: 10.1103/PhysRevB.90.085123[30] Mazin I I, Singh D J, Johannes M D, et al. Unconventional superconductivity with a sign reversal in the order parameter of LaFeAsO1– xFx. Phys Rev Lett, 2008, 101(5), 057003 doi: 10.1103/PhysRevLett.101.057003[31] Ding C, Gong X, Man H, et al. The suppression of Curie temperature by Sr doping in diluted ferromagnetic semiconductor (La1– xSrx)(Zn1– yMny)AsO. EPL, 2014, 107(1), 17004 doi: 10.1209/0295-5075/107/17004[32] Han W, Zhao K, Wang X, et al. Diluted ferromagnetic semiconductor (LaCa)(ZnMn)SbO isostructural to 1111 type iron pnictide superconductors. Sci Chin Phys, Mechan Astron, 2013, 56(11), 2026 doi: 10.1007/s11433-013-5320-1[33] Chen B, Deng Z, Li W, et al. New fluoride-arsenide diluted magnetic semiconductor (Ba, K)F(Zn, Mn)As with independent spin and charge doping. Sci Rep, 2016, 6(1), 36578 doi: 10.1038/srep36578[34] Yang X, Li Y, Shen C,et al. Sr and Mn co-doped LaCuSO: A wide band gap oxide diluted magnetic semiconductor with TC around 200K. Appl Phys Lett, 2013, 103(2), 022410 doi: 10.1063/1.4813540[35] Guo S, Man H, Gong X, et al. (Ba1– xKx)(Cu2– xMnx)Se2: A copper-based bulk form diluted magnetic semiconductor with orthorhombic BaCu2S2-type structure. J Magn Magn Mater, 2016, 400, 295 doi: 10.1016/j.jmmm.2015.07.005[36] Zhao K, Chen B J, Deng Z, et al. (Ca, Na)(Zn, Mn)2As2: A new spin and charge doping decoupled diluted ferromagnetic semiconductor. J Appl Phys, 2014, 116(16), 163906 doi: 10.1063/1.4899190[37] Chen B, Deng Z, Li W, et al. (Sr1– xNax)(Cd1– xMnx)2As2: A new charge and spin doping decoupled diluted magnetic semiconductors with CaAl2Si2-type structure. J Appl Phys, 2016, 120(8), 083902 doi: 10.1063/1.4961565[38] Yang X, Li Y, Zhang P, et al. K and Mn co-doped BaCd2As2: A hexagonal structured bulk diluted magnetic semiconductor with large magnetoresistance. J Appl Phys, 2013, 114(22), 223905 doi: 10.1063/1.4842875[39] Man H, Ding C, Guo S, et al. Ba(Zn1–2xMnxCox)2As2: a bulk form diluted magnetic semiconductor with n-type carriers. arXiv: 1403.4019, 2014[40] Gu B, Maekawa S. Diluted magnetic semiconductors with narrow band gaps. Phys Rev B, 2016, 94(15), 155202 doi: 10.1103/PhysRevB.94.155202[41] Suzuki H, Zhao K, Shibata G, et al. Photoemission and x-ray absorption studies of the isostructural to Fe-based superconductors diluted magnetic semiconductor Ba1– xKx(Zn1– yMny)2As2. Phys Rev B, 2015, 91(14), 140401 doi: 10.1103/PhysRevB.91.140401[42] Suzuki H, Zhao G Q, Zhao K, et al. Fermi surfaces and p-d hybridization in the diluted magnetic semiconductor Ba1– xKx(Zn1– yMny)2As2 studied by soft X-ray angle-resolved photoemission spectroscopy. Phys Rev B, 2015, 92(23), 235120 doi: 10.1103/PhysRevB.92.235120[43] Sun F, Li N N, Chen B J, et al. Pressure effect on the magnetism of the diluted magnetic semiconductor (Ba1– xKx)(Zn1– yMny)2As2 with independent spin and charge doping. Physl Rev B, 2016, 93(22), 224403 doi: 10.1103/PhysRevB.93.224403[44] Sun F, Zhao G Q, Escanhoela C A, et al. Hole doping and pressure effects on the II–II–V-based diluted magnetic semiconductor (Ba1– xKx)(Zn1– yMny)2As2. Phys Rev B, 2017, 95(9), 094412 doi: 10.1103/PhysRevB.95.094412[45] Surmach M A, Chen B J, Deng Z, et al. Weak doping dependence of the antiferromagnetic coupling between nearest-neighbor Mn2+ spins in (Ba1– xKx)(Zn1– yMny)2As2. Phys Rev B, 2018, 97(10), 104418 doi: 10.1103/PhysRevB.97.104418 -
Proportional views






 DownLoad:
DownLoad: