| Citation: |
Zhiguo Sun, Bo Cai, Xi Chen, Wenxian Wei, Xiaoming Li, Dandan Yang, Cuifang Meng, Ye Wu, Haibo Zeng. Prediction and observation of defect-induced room-temperature ferromagnetism in halide perovskites[J]. Journal of Semiconductors, 2020, 41(12): 122501. doi: 10.1088/1674-4926/41/12/122501
****
Z G Sun, B Cai, X Chen, W X Wei, X M Li, D D Yang, C F Meng, Y Wu, H B Zeng, Prediction and observation of defect-induced room-temperature ferromagnetism in halide perovskites[J]. J. Semicond., 2020, 41(12): 122501. doi: 10.1088/1674-4926/41/12/122501.
|
Prediction and observation of defect-induced room-temperature ferromagnetism in halide perovskites
DOI: 10.1088/1674-4926/41/12/122501
More Information
-
Abstract
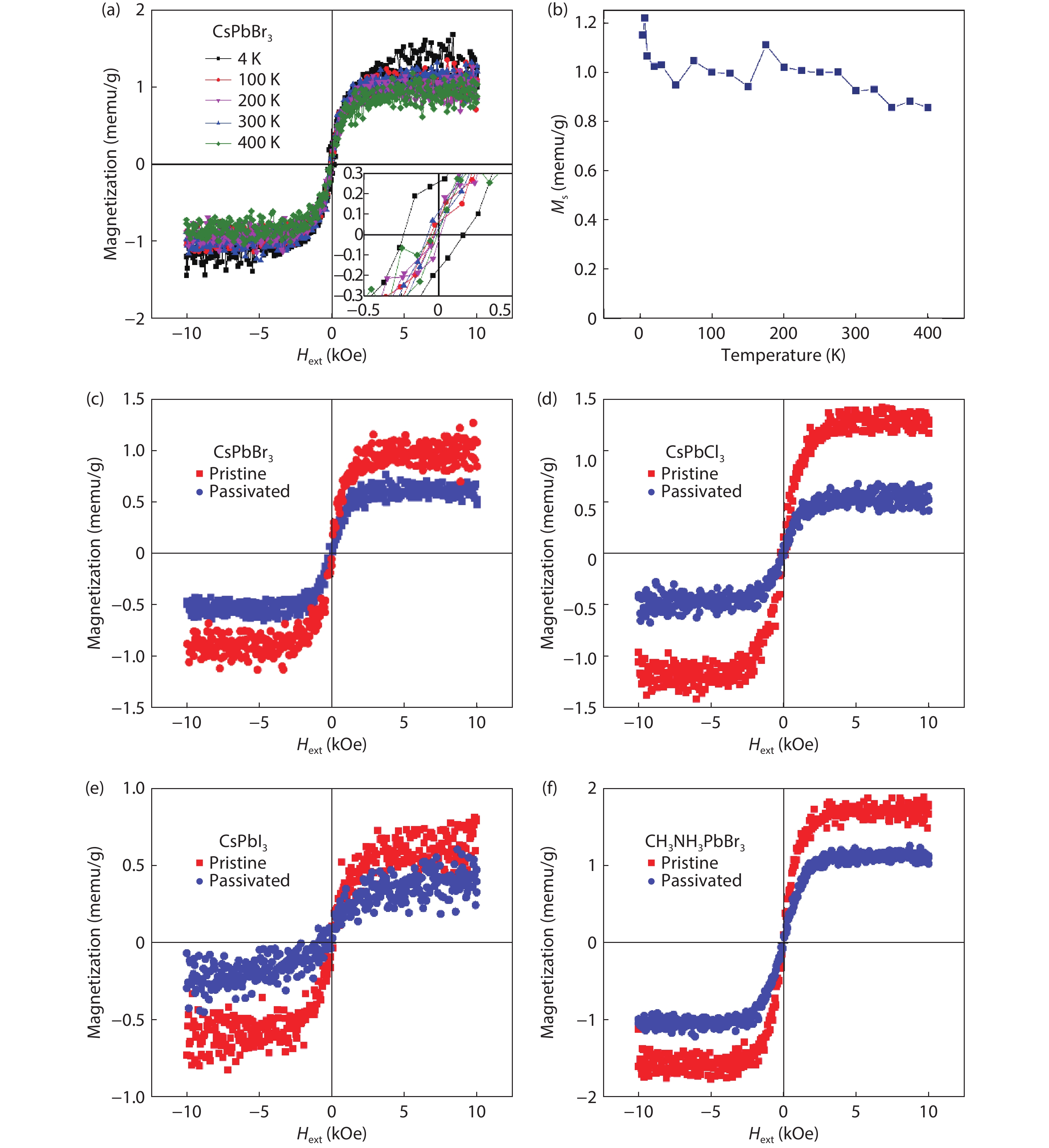
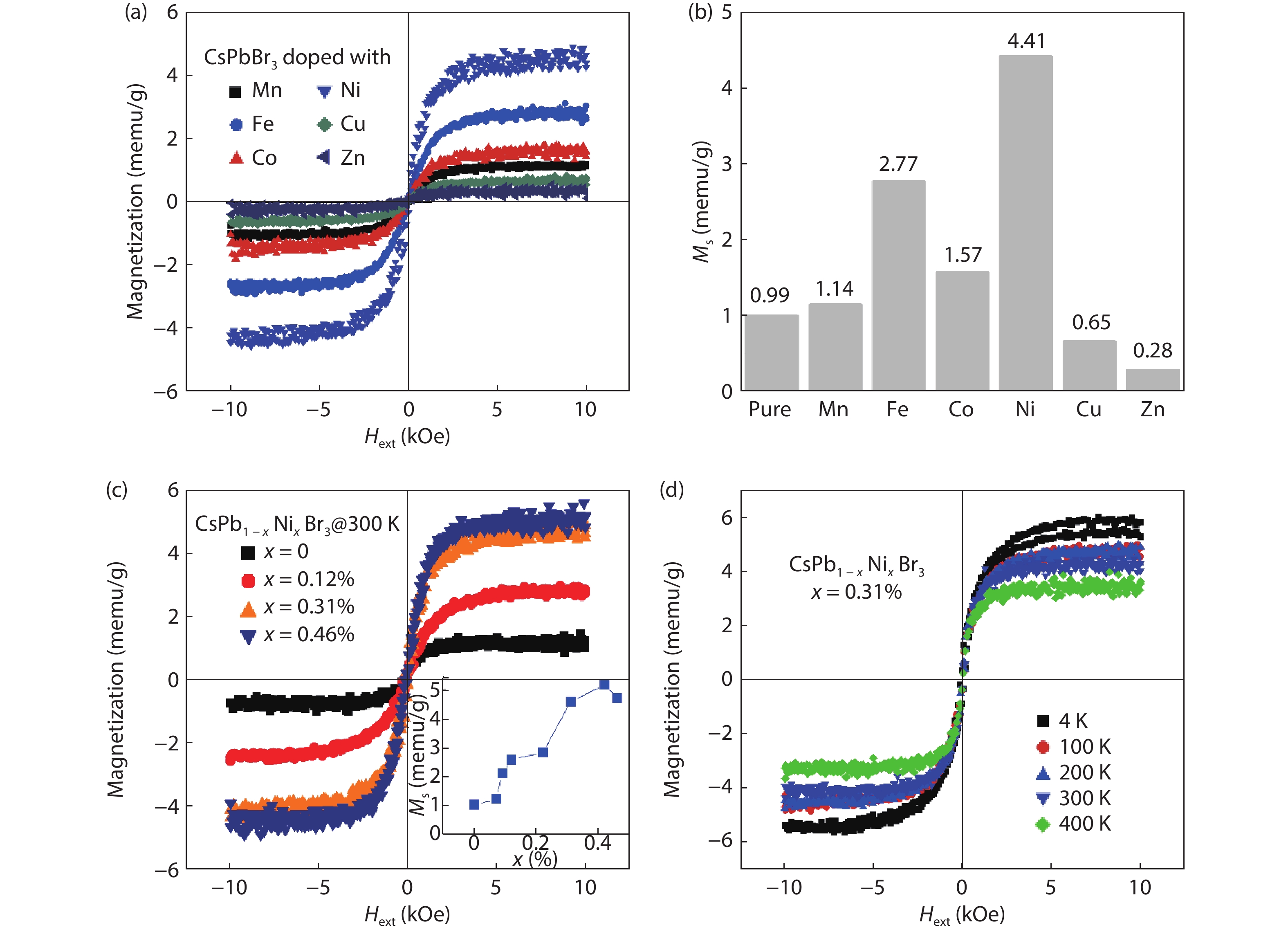
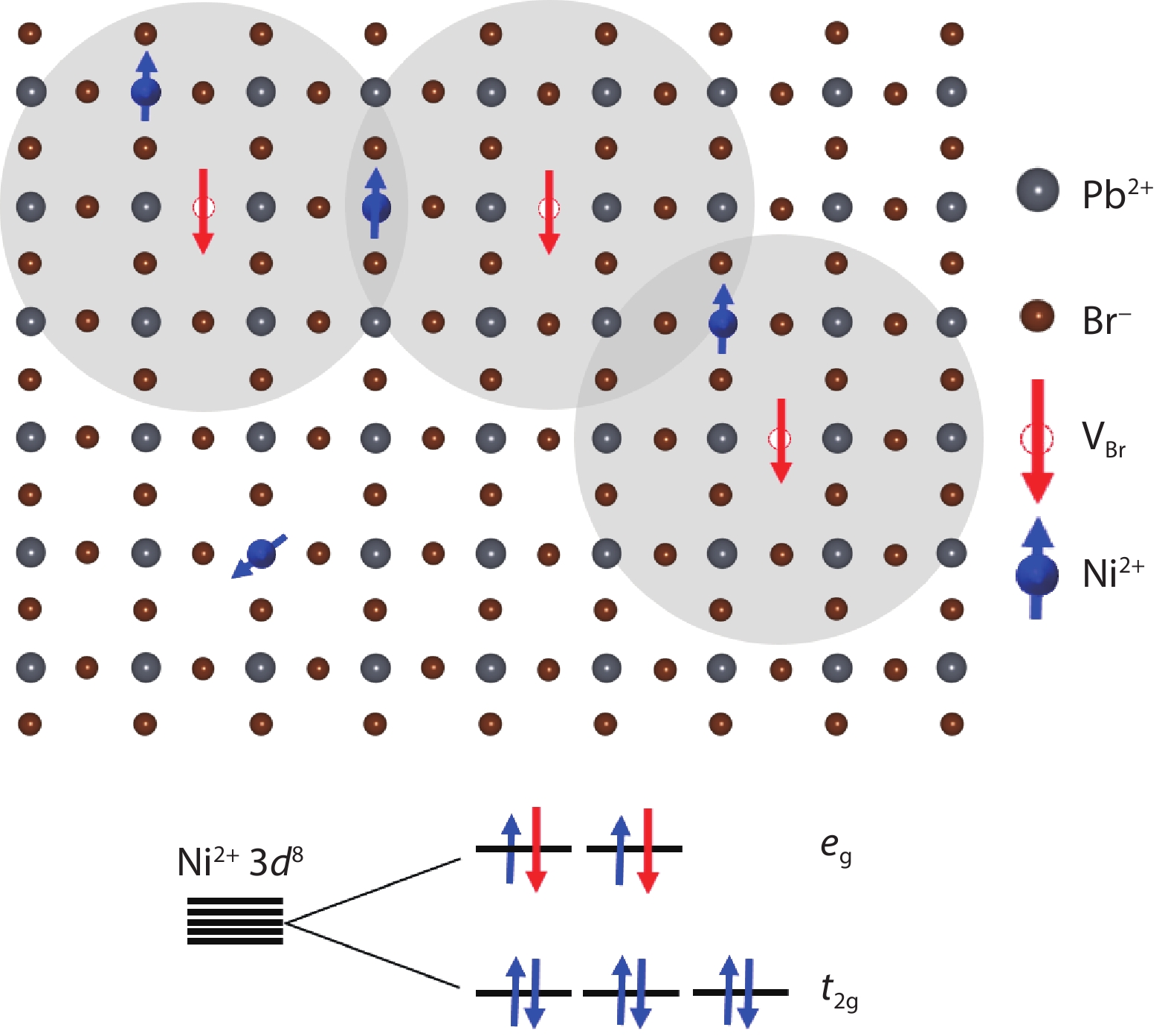
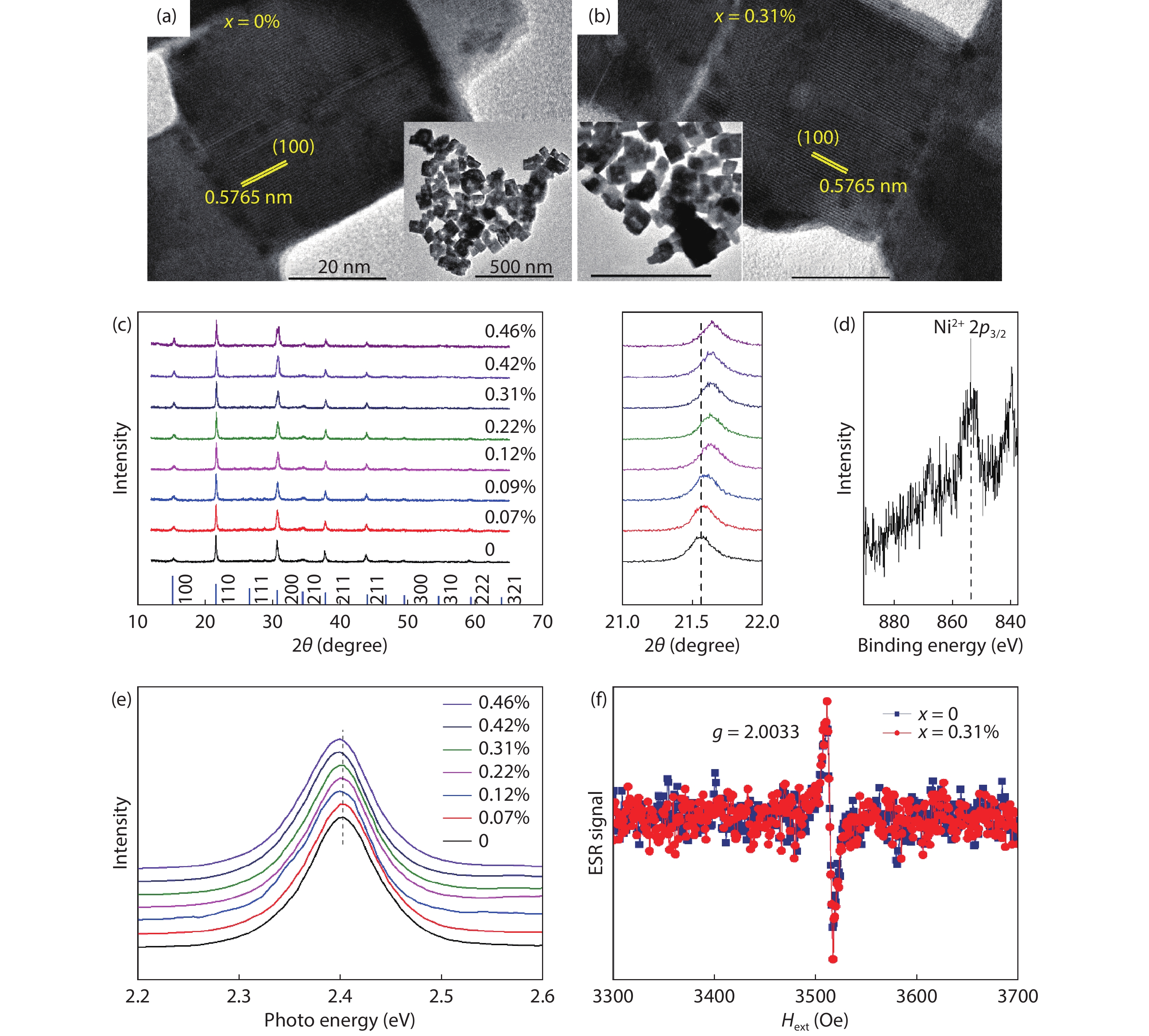
The possibility to induce a macroscopic magnetic moment in lead halide perovskites (LHPs), combined with their excellent optoelectronic properties, is of fundamental interest and has promising spintronic applications. However, these possibilities remain an open question in both theory and experiment. Here, theoretical and experimental studies are performed to explore ferromagnetic states in LHPs originated from lattice defects. First-principle calculations reveal that shallow-level Br vacancies in defective CsPbBr3 can produce spin-splitting states and the coupling between them leads to a ferromagnetic ground state. Experimentally, ferromagnetism at 300 K is observed in room-temperature synthesized CsPbBr3 nanocrystals, but is not observed in hot-injection prepared CsPbBr3 quantum dots and in CsPbBr3 single crystals, highlighting the significance played by vacancy defects. Furthermore, the ferromagnetism in the CsPbBr3 nanocrystals can be enhanced fourfold with Ni2+ ion dopants, due to enhancement of the exchange coupling between magnetic polarons. Room-temperature ferromagnetism is also observed in other LHPs, which suggests that vacancy-induced ferromagnetism may be a universal feature of solution-processed LHPs, which is useful for future spintronic devices. -
References
[1] Žutić I, Fabian J, Das Sarma S. Spintronics: Fundamentals and applications. Rev Mod Phys, 2004, 76, 323 doi: 10.1103/RevModPhys.76.323[2] Qi B, Ólafsson S, Gíslason H P. Vacancy defect-induced d0 ferromagnetism in undoped ZnO nanostructures: Controversial origin and challenges. Prog Mater Sci, 2017, 90, 45 doi: 10.1016/j.pmatsci.2017.07.002[3] Matsumoto Y, Murakami M, Shono T, et al. Room-temperature ferromagnetism in transparent transition metal-doped titanium dioxide. Science, 2001, 291, 854 doi: 10.1126/science.1056186[4] Sharma P, Gupta A, Rao K V, et al. Ferromagnetism above room temperature in bulk and transparent thin films of Mn-doped ZnO. Nat Mater, 2003, 2, 673 doi: 10.1038/nmat984[5] Ogale S B, Choudhary R J, Buban J, et al. High temperature ferromagnetism with a giant magnetic moment in transparent Co-doped SnO2− δ. Phys Rev Lett, 2003, 91, 077205 doi: 10.1103/PhysRevLett.91.077205[6] Fernandes V, Klein J J, Mattoso N, et al. Room temperature ferromagnetism in Co-doped CeO2 films on Si(001). Phys Rev B, 2007, 75, 121304(R doi: 10.1103/PhysRevB.75.121304[7] Reed M L, El-Masry N A, Stadelmaier H H, et al. Room temperature ferromagnetic properties of (Ga, Mn)N. Appl Phys Lett, 2001, 79, 3473 doi: 10.1063/1.1419231[8] Coey J M D. d0 Ferromagnetism. Solid State Sci, 2005, 7, 660 doi: 10.1016/j.solidstatesciences.2004.11.012[9] Sundaresan A, Bhargavi R, Rangarajan N, et al. Ferromagnetism as a universal feature of nanoparticles of the otherwise nonmagnetic oxides. Phys Rev B, 2006, 74, 161306 doi: 10.1103/PhysRevB.74.161306[10] Rumaiz A K, Ali B, Ceylan A, et al. Experimental studies on vacancy induced ferromagnetism in undoped TiO2. Solid State Commun, 2007, 144, 334 doi: 10.1016/j.ssc.2007.08.034[11] Zhan P, Wang W P, Liu C, et al. Oxygen vacancy–induced ferromagnetism in un-doped ZnO thin films. J Appl Phys, 2012, 111, 033501 doi: 10.1063/1.3679560[12] Niu G, Hildebrandt E, Schubert M A, et al. Oxygen vacancy induced room temperature ferromagnetism in Pr-doped CeO2 thin films on silicon. ACS Appl Mater Interfaces, 2014, 6, 17496 doi: 10.1021/am502238w[13] Roul B, Rajpalke M K, Bhat T N, et al. Experimental evidence of Ga-vacancy induced room temperature ferromagnetic behavior in GaN films. Appl Phys Lett, 2011, 99, 162512 doi: 10.1063/1.3654151[14] Wang H X, Zong Z C, Yan Y. Mechanism of multi-defect induced ferromagnetism in undoped rutile TiO2. J Appl Phys, 2014, 115, 233909 doi: 10.1063/1.4884223[15] Han X P, Lee J, Yoo H I. Oxygen-vacancy-induced ferromagnetism in CeO2 from first principles. Phys Rev B, 2009, 79, 100403 doi: 10.1103/PhysRevB.79.100403[16] Dev P, Xue Y, Zhang P H. Defect-Induced intrinsic magnetism in wide-gap III nitrides. Phys Rev Lett, 2008, 100, 117204 doi: 10.1103/PhysRevLett.100.117204[17] Wang Y R, Piao J Y, Xing G Z, et al. Zn vacancy induced ferromagnetism in K doped ZnO. J Mater Chem C, 2015, 3, 11953 doi: 10.1039/C5TC02936H[18] Ahn C H, Kim Y Y, Kim D C, et al. Erratum: “A comparative analysis of deep level emission in ZnO layers deposited by various methods ” [J. Appl. Phys. 105, 013502 (2009)]. J Appl Phys, 2009, 105, 089902 doi: 10.1063/1.3112042[19] Fabbri F, Villani M, Catellani A, et al. Zn vacancy induced green luminescence on non-polar surfaces in ZnO nanostructures. Sci Rep, 2014, 4, 5158 doi: 10.1038/srep05158[20] Morgan B J, Watson G W. Polaronic trapping of electrons and holes by native defects in anatase TiO2. Phys Rev B, 2009, 80, 233102 doi: 10.1103/PhysRevB.80.233102[21] Lyons J L, van de Walle C G. Computationally predicted energies and properties of defects in GaN. npj Comput Mater, 2017, 3, 12 doi: 10.1038/s41524-017-0014-2[22] Akkerman Q A, Rainò G, Kovalenko M V, et al. Genesis, challenges and opportunities for colloidal lead halide perovskite nanocrystals. Nat Mater, 2018, 17, 394 doi: 10.1038/s41563-018-0018-4[23] Walsh A, Scanlon D O, Chen S Y, et al. Self-regulation mechanism for charged point defects in hybrid halide perovskites. Angew Chem Int Ed, 2015, 54, 1791 doi: 10.1002/anie.201409740[24] Dong Q F, Fang Y J, Shao Y C, et al. Solar cells. Electron-hole diffusion lengths > 175 μm in solution-grown CH3NH3PbI3 single crystals. Science, 2015, 347, 967 doi: 10.1126/science.aaa5760[25] Dutta A, Behera R K, Pal P, et al. Near-unity photoluminescence quantum efficiency for all CsPbX3 (X = Cl, Br, and I) perovskite nanocrystals: A generic synthesis approach. Angew Chem Int Ed, 2019, 58, 5552 doi: 10.1002/anie.201900374[26] Jeon N J, Na H, Jung E H, et al. A fluorene-terminated hole-transporting material for highly efficient and stable perovskite solar cells. Nat Energy, 2018, 3, 682 doi: 10.1038/s41560-018-0200-6[27] Lin K, Xing J, Quan L N, et al. Perovskite light-emitting diodes with external quantum efficiency exceeding 20 per cent. Nature, 2018, 562, 245 doi: 10.1038/s41586-018-0575-3[28] Cao Y, Wang N N, Tian H, et al. Perovskite light-emitting diodes based on spontaneously formed submicrometre-scale structures. Nature, 2018, 562, 249 doi: 10.1038/s41586-018-0576-2[29] Yin W J, Shi T T, Yan Y F. Unusual defect physics in CH3NH3PbI3 perovskite solar cell absorber. Appl Phys Lett, 2014, 104, 063903 doi: 10.1063/1.4864778[30] Kang J, Wang L W. High defect tolerance in lead halide perovskite CsPbBr3. J Phys Chem Lett, 2017, 8, 489 doi: 10.1021/acs.jpclett.6b02800[31] Zhai Y X, Baniya S, Zhang C, et al. Giant Rashba splitting in 2D organic-inorganic halide perovskites measured by transient spectroscopies. Sci Adv, 2017, 3, e1700704 doi: 10.1126/sciadv.1700704[32] Zhang C, Sun D L, Yu Z G, et al. Field-induced spin splitting and anomalous photoluminescence circular polarization in CH3NH3PbI3 films at high magnetic field. Phys Rev B, 2018, 97, 134412 doi: 10.1103/PhysRevB.97.134412[33] Sun D L, Zhang C, Kavand M, et al. Surface-enhanced spin current to charge current conversion efficiency in CH3NH3PbBr3-based devices. J Chem Phys, 2019, 151, 174709 doi: 10.1063/1.5125230[34] Wang J, Zhang C, Liu H, et al. Spin-optoelectronic devices based on hybrid organic-inorganic trihalide perovskites. Nat Commun, 2019, 10, 129 doi: 10.1038/s41467-018-07952-x[35] Kresse, Furthmüller. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B, 1996, 54, 11169 doi: 10.1103/PhysRevB.54.11169[36] Perdew J P, Ruzsinszky A, Csonka G I, et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys Rev Lett, 2008, 100, 136406 doi: 10.1103/PhysRevLett.100.136406[37] Jakes P, Zimmermann J, von Seggern H, et al. Eu2+-doped CsBr photostimulable X-ray storage phosphors: Analysis of defect structure by high-frequency EPR. Funct Mater Lett, 2014, 7, 1350073 doi: 10.1142/S1793604713500732[38] Coey M, Ackland K, Venkatesan M, et al. Collective magnetic response of CeO2 nanoparticles. Nat Phys, 2016, 12, 694 doi: 10.1038/nphys3676[39] Coey J M D. Magnetism in d0 oxides. Nat Mater, 2019, 18, 652 doi: 10.1038/s41563-019-0365-9[40] Yuan Y B, Huang J S. Ion migration in organometal trihalide perovskite and its impact on photovoltaic efficiency and stability. Acc Chem Res, 2016, 49, 286 doi: 10.1021/acs.accounts.5b00420[41] Yong Z J, Guo S Q, Ma J P, et al. Doping-enhanced short-range order of perovskite nanocrystals for near-unity violet luminescence quantum yield. J Am Chem Soc, 2018, 140, 9942 doi: 10.1021/jacs.8b04763[42] Kaminski A, Das Sarma S. Polaron percolation in diluted magnetic semiconductors. Phys Rev Lett, 2002, 88, 247202 doi: 10.1103/PhysRevLett.88.247202[43] Coey J M D, Venkatesan M, Fitzgerald C B. Donor impurity band exchange in dilute ferromagnetic oxides. Nat Mater, 2005, 4, 173 doi: 10.1038/nmat1310[44] Kang Y, Han S. Intrinsic carrier mobility of cesium lead halide perovskites. Phys Rev Appl, 2018, 10, 044013 doi: 10.1103/PhysRevApplied.10.044013[45] Pan F, Song C, Liu X J, et al. Ferromagnetism and possible application in spintronics of transition-metal-doped ZnO films. Mater Sci Eng R, 2008, 62, 1 doi: 10.1016/j.mser.2008.04.002 -
Supplements
 20040016suppl.pdf
20040016suppl.pdf

-
Proportional views





 DownLoad:
DownLoad: