| Citation: |
Shaojie Li, Peide Han. Effects of high temperature annealing and laser irradiation on activation rate of phosphorus[J]. Journal of Semiconductors, 2020, 41(12): 122701. doi: 10.1088/1674-4926/41/12/122701
****
S J Li, P D Han, Effects of high temperature annealing and laser irradiation on activation rate of phosphorus[J]. J. Semicond., 2020, 41(12): 122701. doi: 10.1088/1674-4926/41/12/122701.
|
Effects of high temperature annealing and laser irradiation on activation rate of phosphorus
DOI: 10.1088/1674-4926/41/12/122701
More Information
-
Abstract
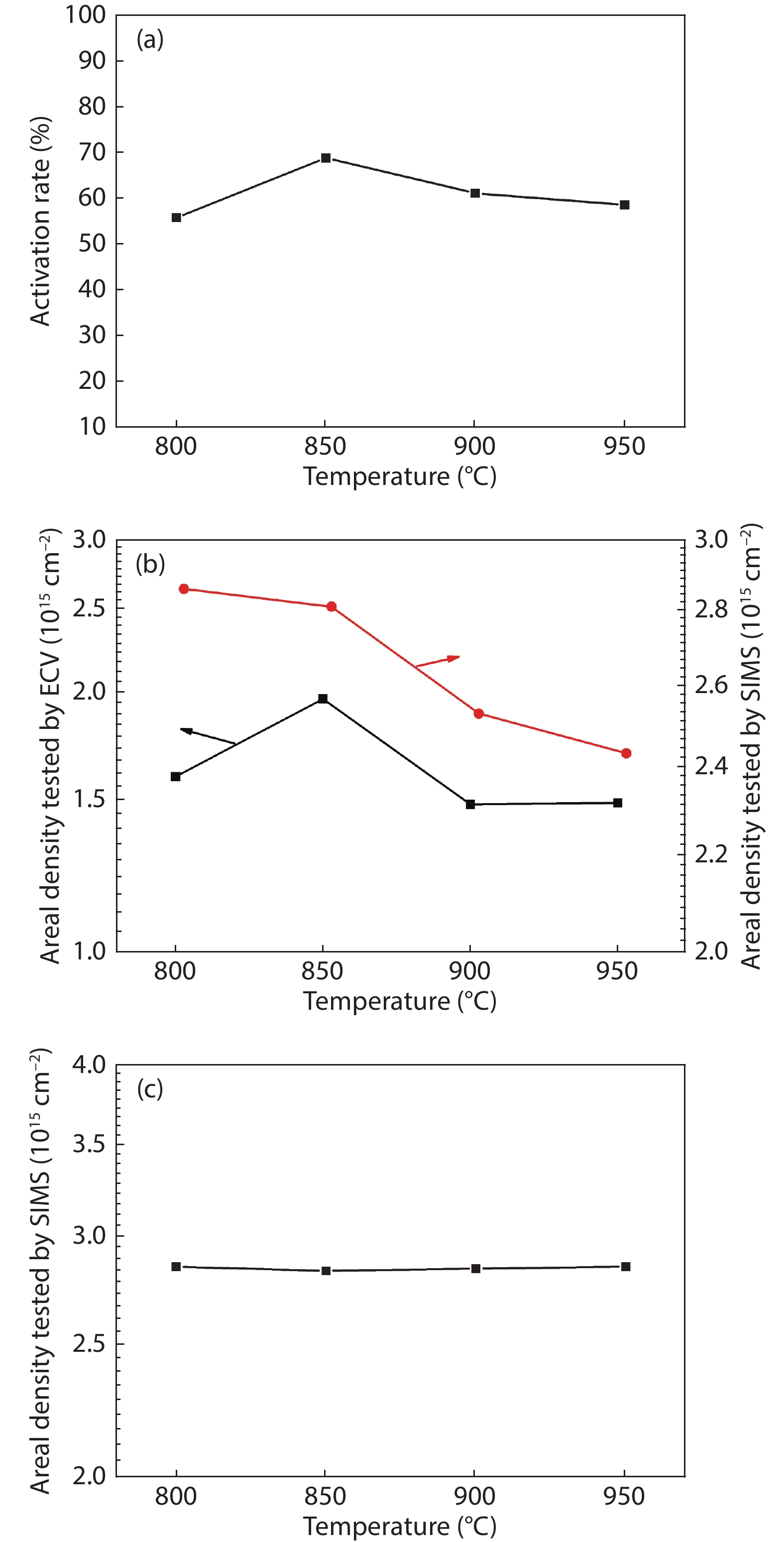
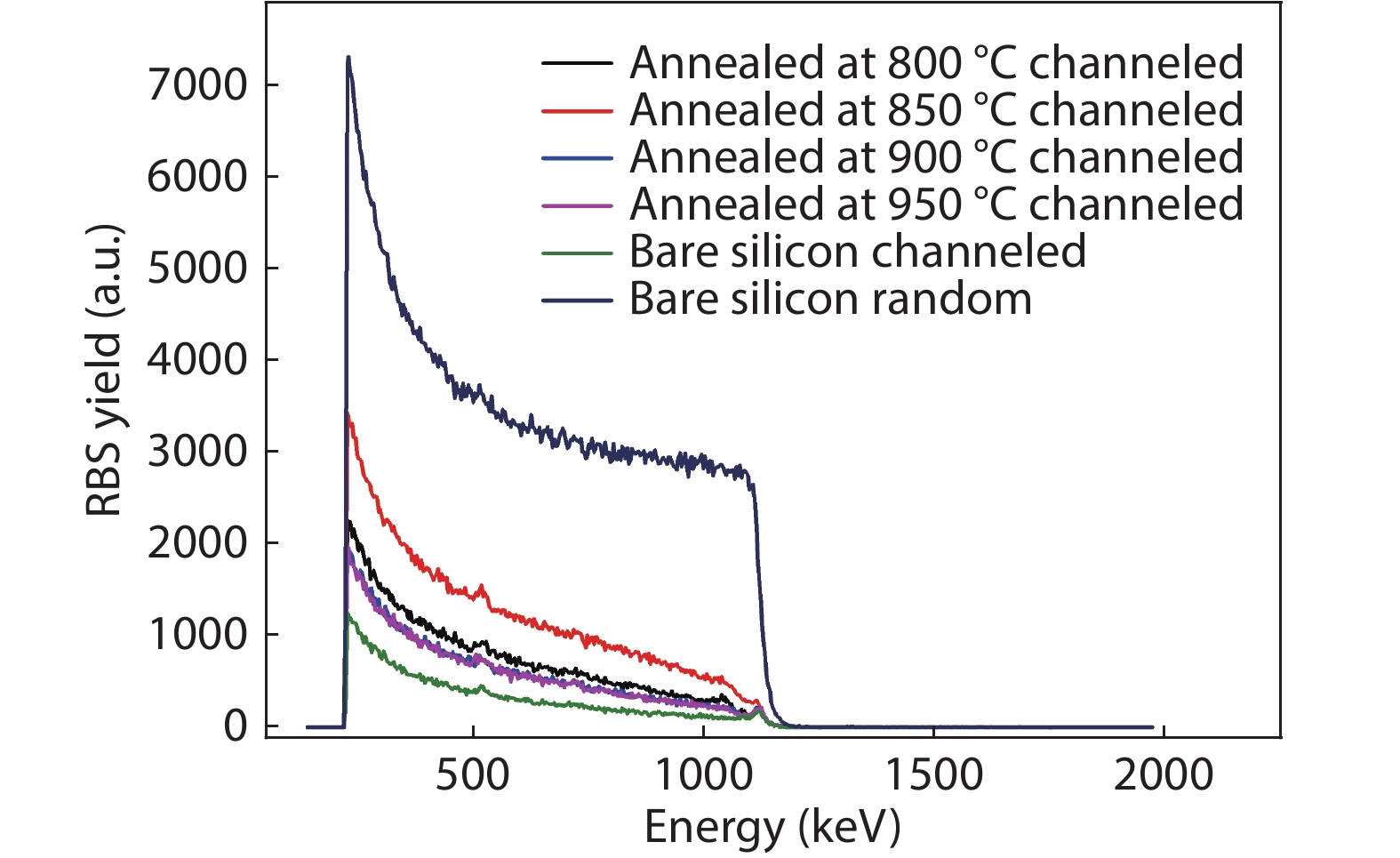
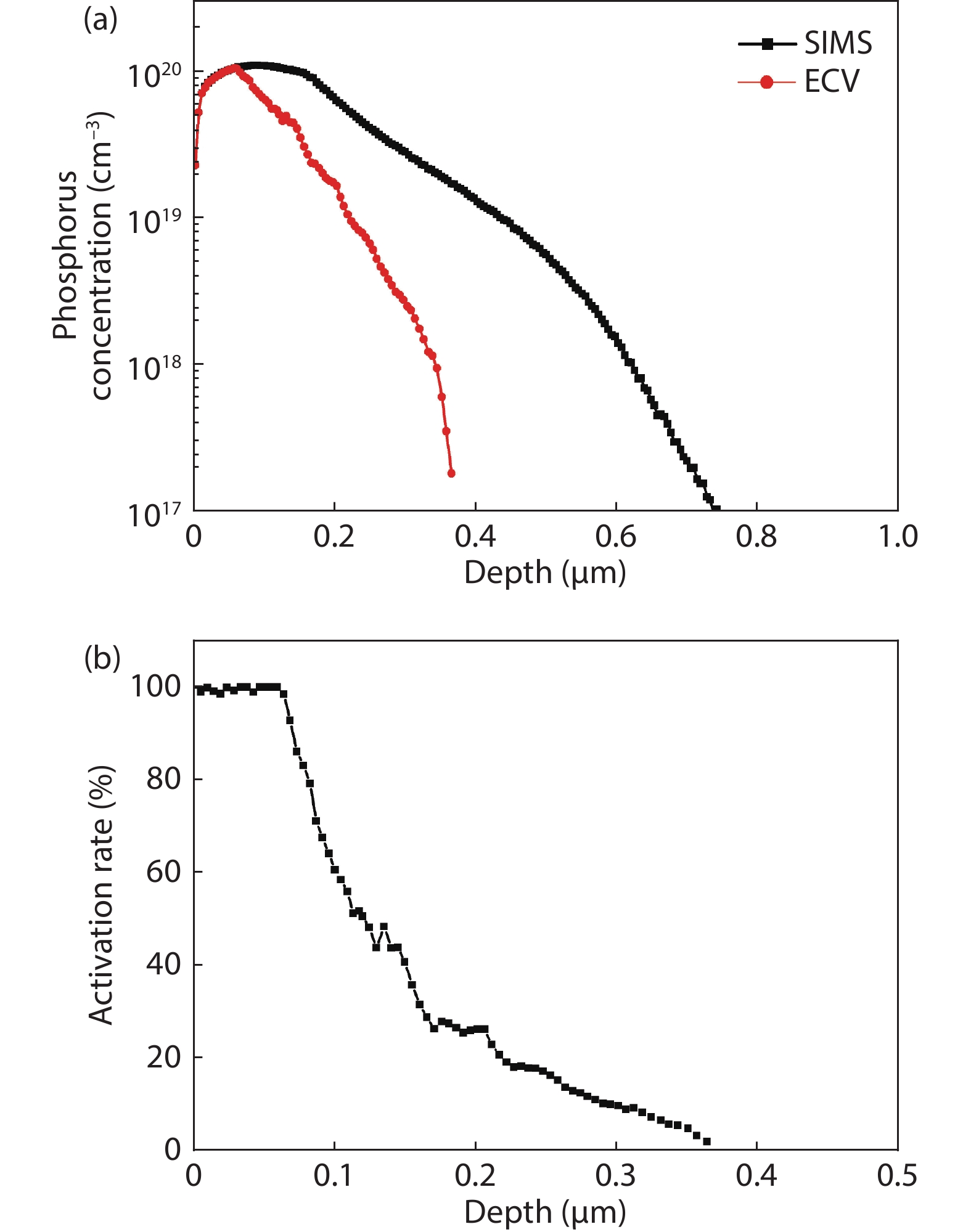
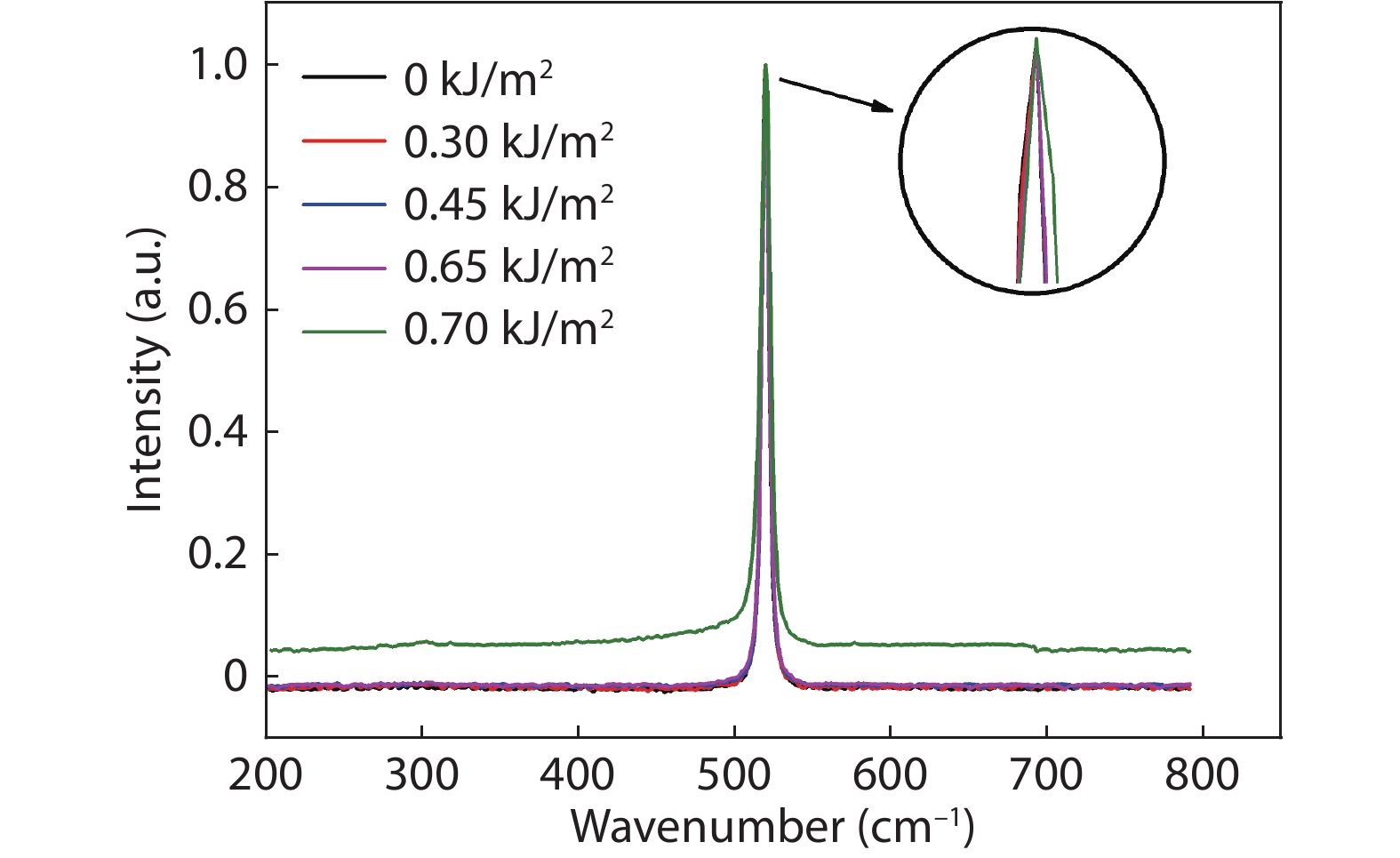
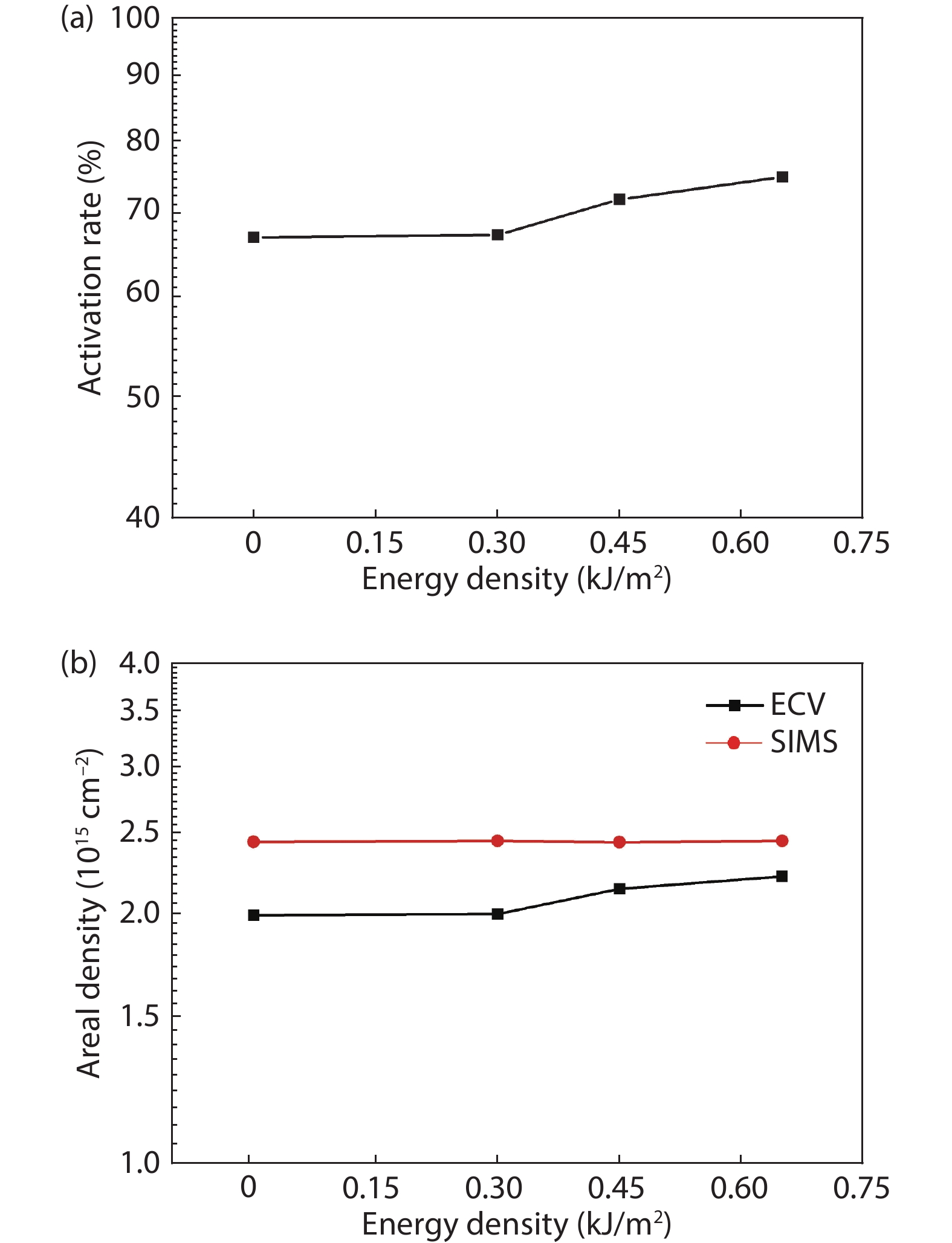
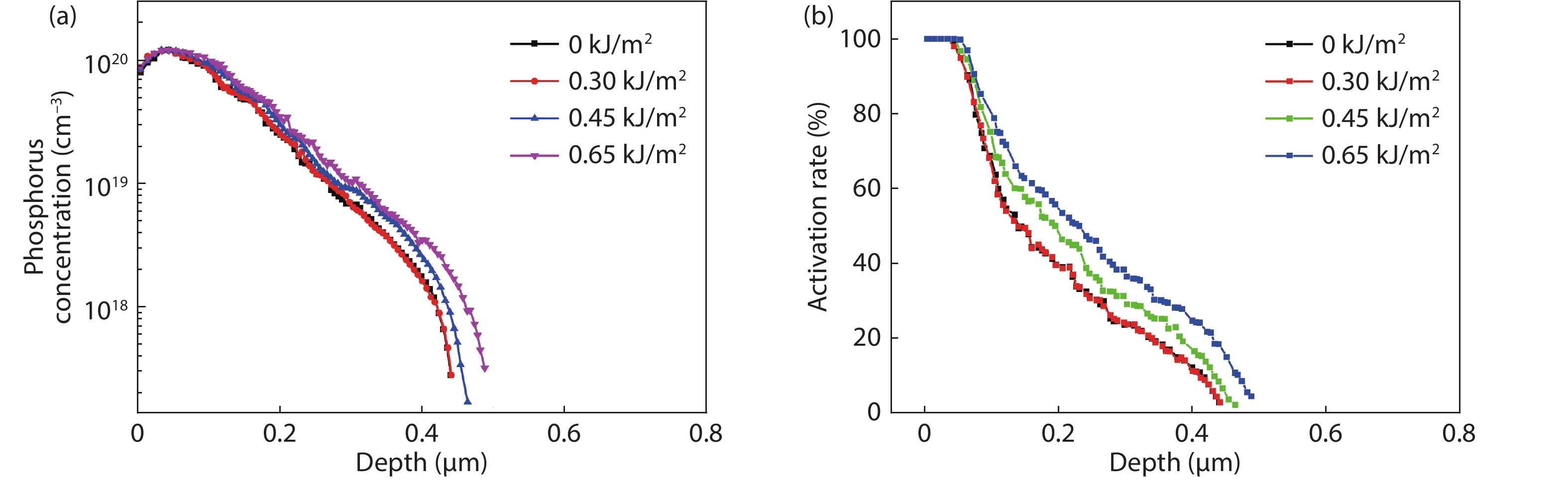
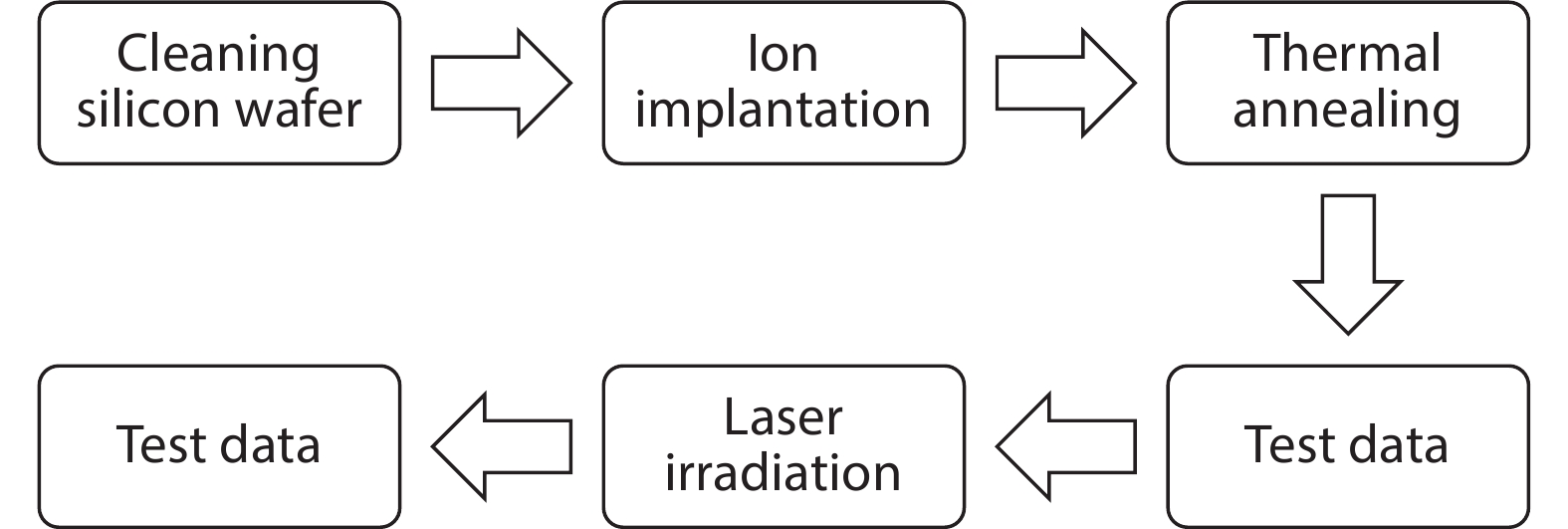
Thermal annealing and laser irradiation were used to study the activation rate of phosphorus in silicon after ion implantation. The activation rate refers to the ratio of activated impurity number to the total impurity number in the sample. After injecting phosphorus with the dose and energy (energy = 55 keV, dose = 3 × 1015 cm–2), the samples were annealed at different temperatures, and laser irradiation experiments were performed after annealing. The experimental results showed that the activation rate of phosphorus was the highest at 850 °C, and the highest activation rate was 67%. Upon femtosecond laser irradiation samples after thermal annealing, while keeping the crystalline silicon surface without damage, the activation rate was improved. When the energy-flux density of the femtosecond laser was 0.65 kJ/cm2, the activation rate was the highest, increasing from 67% to 74.81%. -
References
[1] Hofker W K. Implantation of boron in silicon. Philips Res Rep, 1975, 15(3), 189 doi: 10.1007/BF02726346[2] Skorupa W, Wieser E, Groetzschel R, et al. High energy implantation and annealing of phosphorus in silicon. Nucl Instrum Methods Phys Res, 1987, 19/20(Part1), 335 doi: 10.1016/S0168-583X(87)80068-X[3] Kisielewicz M A. The damage-dependent atom and carrier profiles in phosphorus-implanted silicon. Thin Solid Films, 1983, 109(1), 11 doi: 10.1016/0040-6090(83)90026-3[4] Tsai M Y, Streetman B G. Recrystallization of implanted amorphous silicon layers. I. Electrical properties of silicon implanted with BF+2 or Si++B+. J Appl Phys, 1979, 50(1), 183 doi: 10.1063/1.325688[5] Landi E, Guimaraes S, Solmi S. Influence of nucleation on the kinetics of boron precipitation in silicon. Appl Phys A, 1987, 44(2), 135 doi: 10.1007/BF00626414[6] Solmi S, Landi E, Baruffaldi F. High-concentration boron diffusion in silicon: Simulation of the precipitation phenomena. J Appl Phys, 1990, 68(7), 3250 doi: 10.1063/1.346376[7] Stolk P A, Gossmann H J, Eaglesham D J, et al. Physical mechanisms of transient enhanced dopant diffusion in ion-implanted silicon. J Appl Phys, 1997, 81(9), 6031 doi: 10.1063/1.364452[8] Suzuki K, Tada Y, Kataoka Y, et al. Maximum active concentration of ion-implanted phosphorus during solid-phase epitaxial recrystallization. IEEE Trans Electron Devices, 2007, 54(8), 1985 doi: 10.1109/TED.2007.901157[9] Hadjersi T. Annihilation kinetics of defects induced by phosphorus ion implantation in silicon. Appl Surf Sci, 2001, 185(1/2), 140 doi: 10.1016/S0169-4332(01)00776-0[10] Wu C, Crouch C H, Zhao L, et al. Near-unity below-band-gap absorption by microstructured silicon. Appl Phys Lett, 2001, 78(13), 1850 doi: 10.1063/1.1358846[11] Crouch C H, Carey J E, Shen M, et al. Infrared absorption by sulfur-doped silicon formed by femtosecond laser irradiation. Appl Phys A, 2004, 79(7), 1635 doi: 10.1007/s00339-004-2676-0[12] Köhler J R, Eisele S J. Phosphorus out-diffusion in laser molten silicon. J Appl Phys, 2015, 117(14), 145701 doi: 10.1063/1.4917048[13] Winkler M T, Recht D, Sher M J, et al. Insulator-to-metal transition in sulfur-doped silicon. Phys Rev Lett, 2011, 106(17), 51 doi: 10.1103/PhysRevLett.106.178701[14] Normann H B, Svensson B G, Monakhov E. Formation of shallow front emitters for solar cells by rapid thermal processing. Phys Status Solidi, 2012, 9(11), 2138 doi: 10.1002/pssc.201200202[15] Uematsu M. Simulation of boron, phosphorus, and arsenic diffusion in silicon based on an integrated diffusion model, and the anomalous phosphorus diffusion mechanism. J Appl Phys, 1997, 82(5), 2228 doi: 10.1063/1.366030[16] Othonos A. Probing ultrafast carrier and phonon dynamics in semiconductors. J Appl Phys, 1998, 83(4), 1789 doi: 10.1063/1.367411[17] Cerva H. Comparison of transmission electron microscope cross sections of amorphous regions in ion implanted silicon with point-defect density calculations. J Electrochem Soc, 1992, 139(12), 3631 doi: 10.1149/1.2069134[18] Uematsu M. Implantation species dependence of transient enhanced diffusion in silicon. J Appl Phys, 1998, 83(1), 120 doi: 10.1063/1.366708[19] Schroer E, Uematsu M. Simulation of clustering and pile-up during post-implantation annealing of phosphorus in silicon. Jpn J Appl Phys, 1999, 38(1A), 7 doi: 10.1143/jjap.38.7[20] Uematsu M. Simulation of clustering and transient enhanced diffusion of boron in silicon. J Appl Phys, 1998, 84(9), 4781 doi: 10.1063/1.368720[21] Uematsu M. Simulation of high-concentration phosphorus diffusion in silicon taking into account phosphorus clustering and pile-up. Jpn J Appl Phys, 1999, 38(11), 6188 doi: 10.1143/JJAP.38.6188[22] Mayer J W, Nicolet M, Chu W K. Backscattering spectrometry. Academic Press, 1978[23] Sundaram S K, Mazur E. Inducing and probing non-thermal transitions in semiconductors using femtosecond laser pulses. Nat Mater, 2002, 1(4), 271 doi: 10.1038/nmat767[24] Silvestrelli P L, Alavi A, Parrinello M, et al. Ab initio molecular dynamics simulation of laser melting of silicon. Phys Rev Lett, 1996, 77(15), 3149 doi: 10.1103/PhysRevLett.77.3149[25] Lo H W, Compaan A. Raman measurement of lattice temperature during pulsed laser heating of silicon. Phys Rev Lett, 1980, 44(24), 1604 doi: 10.1103/PhysRevLett.44.1604 -
Proportional views





 DownLoad:
DownLoad: