| Citation: |
Xuefen Cai, Peng Zhang, Su-Huai Wei. Revisit of the band gaps of rutile SnO2 and TiO2: a first-principles study[J]. Journal of Semiconductors, 2019, 40(9): 092101. doi: 10.1088/1674-4926/40/9/092101
****
X F Cai, P Zhang, S H Wei, Revisit of the band gaps of rutile SnO2 and TiO2: a first-principles study[J]. J. Semicond., 2019, 40(9): 092101. doi: 10.1088/1674-4926/40/9/092101.
|
Revisit of the band gaps of rutile SnO2 and TiO2: a first-principles study
DOI: 10.1088/1674-4926/40/9/092101
More Information
-
Abstract
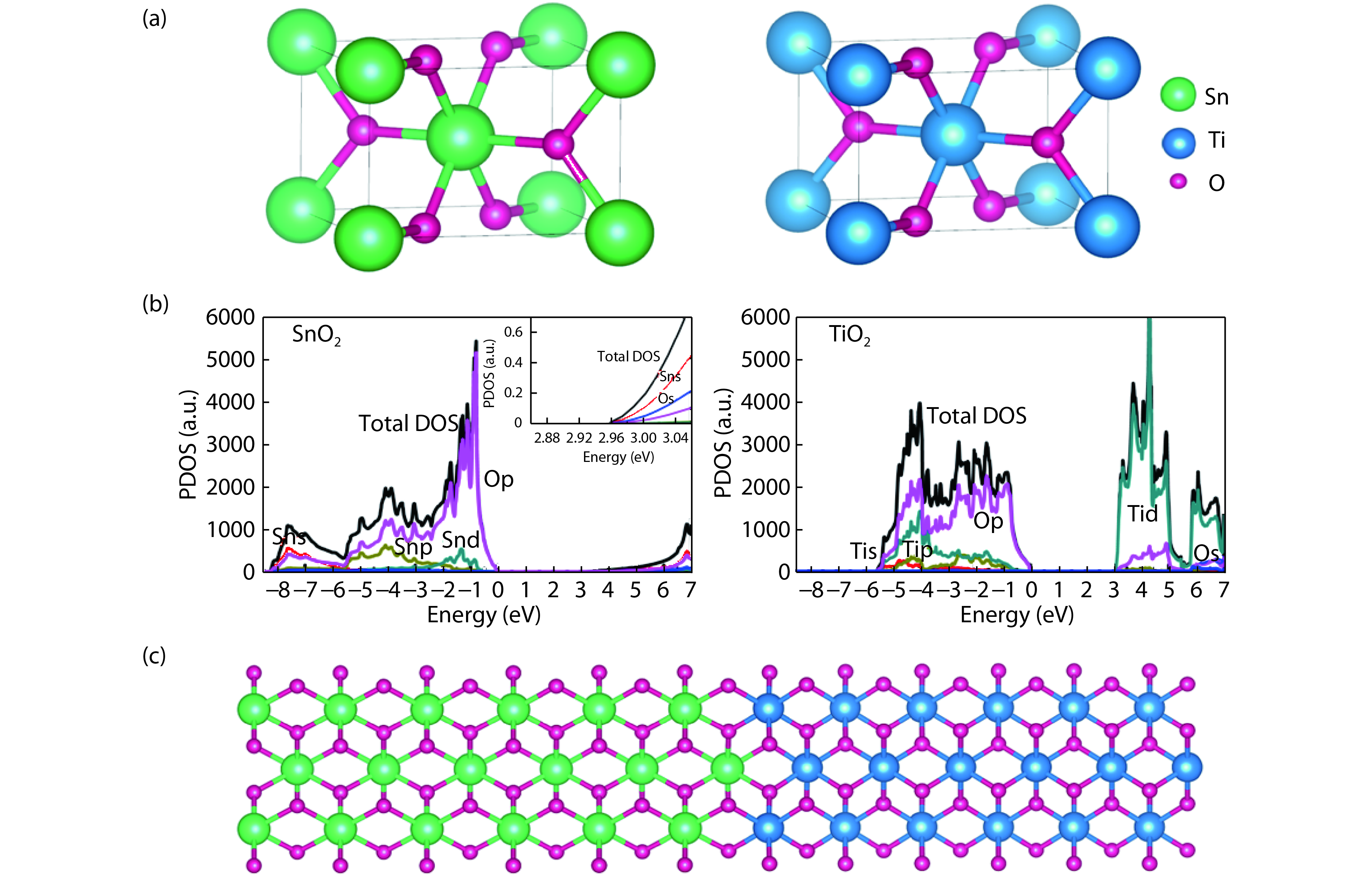
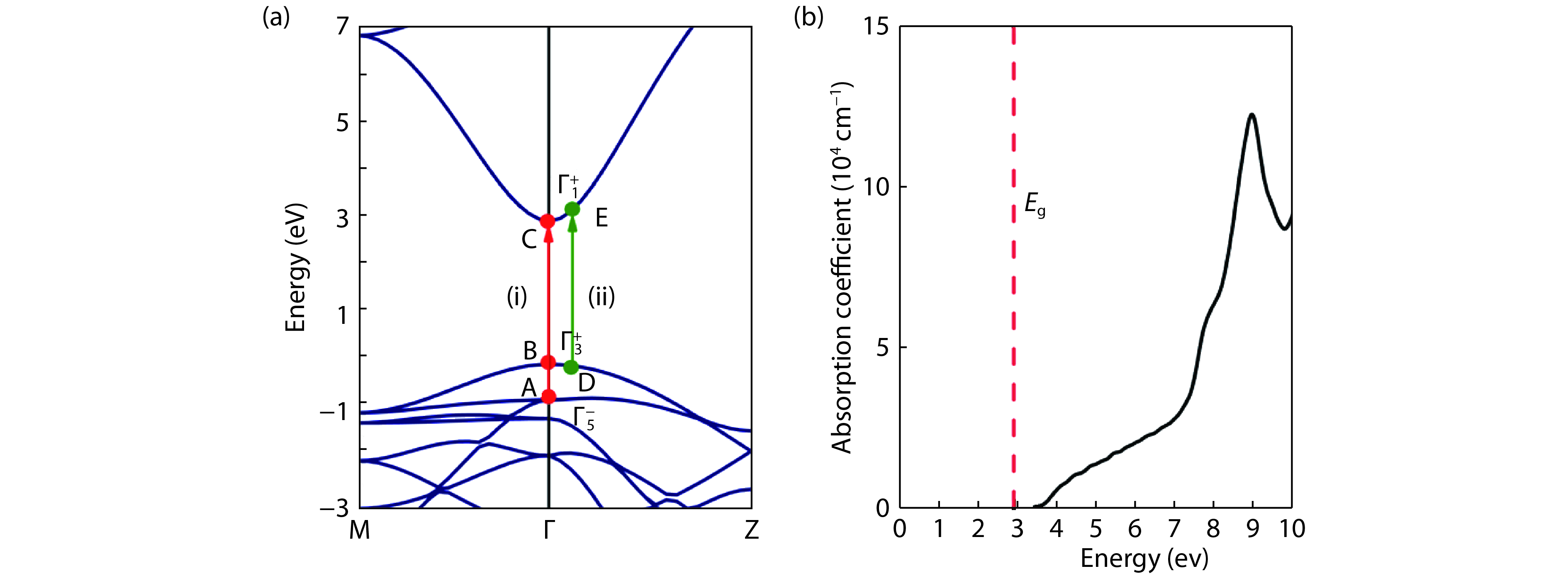
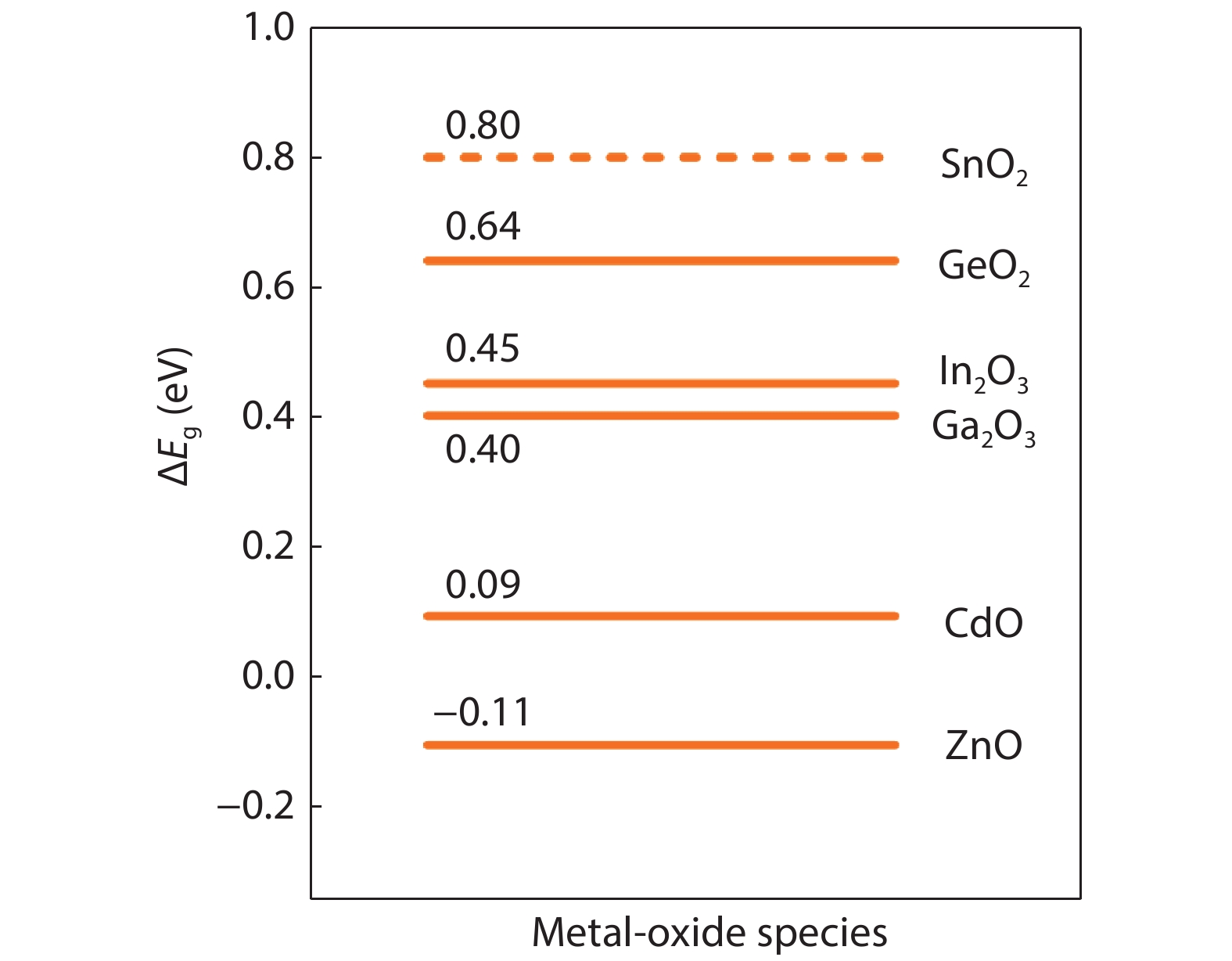
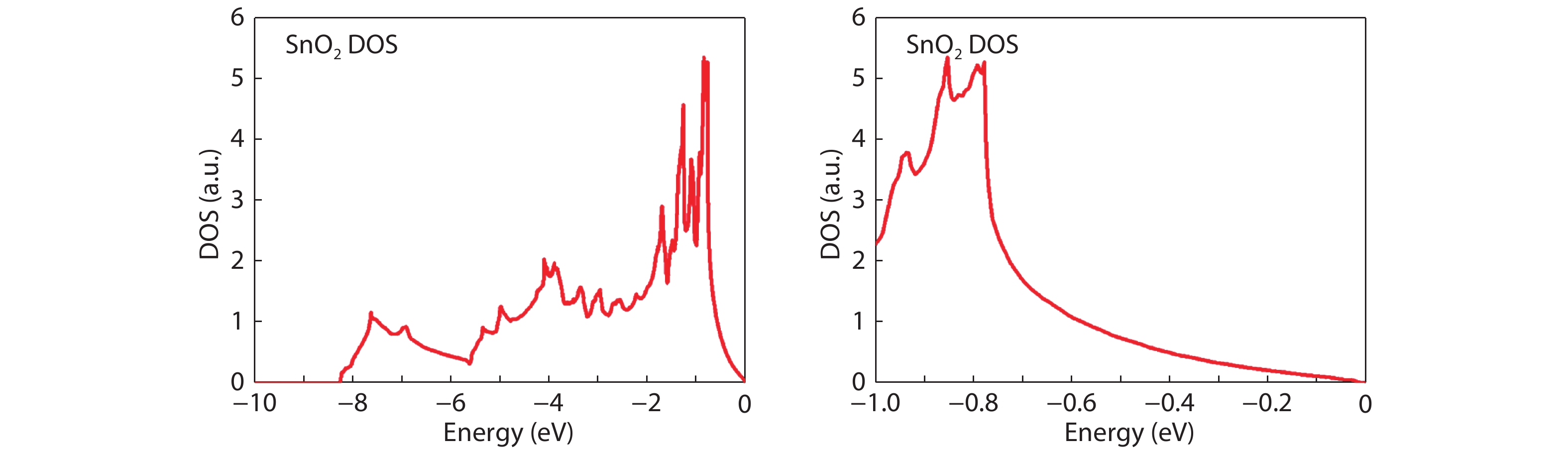
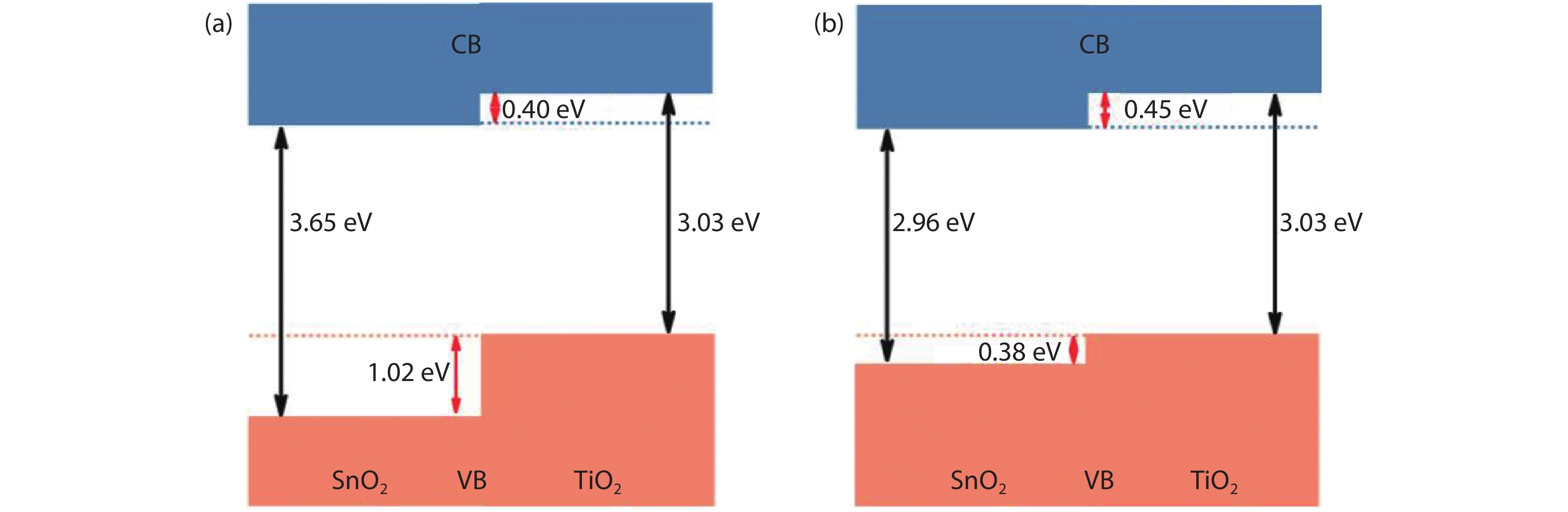
From the recent experimentally observed conduction band offset and previously reported band gaps, one may deduce that the valence band offset between rutile SnO2 and TiO2 is around 1 eV, with TiO2 having a higher valence band maximum. This implication sharply contradicts the fact that the two compounds have the same rutile structure and the Γ3+ VBM state is mostly an oxygen p state with a small amount of cation d character, thus one would expect that SnO2 and TiO2 should have small valence band offset. If the valence band offset between SnO2 and TiO2 is indeed small, one may question the correctness of the previously reported band gaps of SnO2 and TiO2. In this paper, using first-principles calculations with different levels of computational methods and functionals within the density functional theory, we reinvestigate the long-standing band gap problem for SnO2. Our analysis suggests that the fundamental band gap of SnO2 should be similar to that of TiO2, i.e., around 3.0 eV. This value is significantly smaller than the previously reported value of about 3.6 eV, which can be attributed as the optical band gap of this material. Similar to what has been found in In2O3, the discrepancy between the fundamental and optical gaps of SnO2 can be ascribed to the inversion symmetry of its crystal structure and the resultant dipole-forbidden transitions between its band edges. Our results are consistent with most of the optical and electrical measurements of the band gaps and band offset between SnO2 and TiO2, thus provide new understanding of the band structure and optical properties of SnO2. Experimental tests of our predictions are called for.-
Keywords:
- SnO2,
- TiO2,
- band gap,
- band offset,
- dipole-forbidden transition
-
References
[1] Chopra K, Major S, Pandya D. Transparent conductors-a status review. Thin Solid Films, 1983, 102, 1 doi: 10.1016/0040-6090(83)90256-0[2] Nomura K, Ohta H, Ueda K, et al. Thin-film transistor fabricated in single-crystalline transparent oxide semiconductor. Science, 2003, 300, 1269 doi: 10.1126/science.1083212[3] Wager J F. Transparent electronics. Science, 2003, 300, 1245 doi: 10.1126/science.1085276[4] Nomura K, Ohta H, Takagi A, et al. Room-temperature fabrication of transparent flexible thin-film transistors using amorphous oxide semiconductors. Nature, 2004, 432, 488 doi: 10.1038/nature03090[5] Minami T. Transparent conducting oxide semiconductors for transparent electrodes. Semicond Sci Technol, 2005, 20, S35 doi: 10.1088/0268-1242/20/4/004[6] Granqvist C G. Transparent conductors as solar energy materials: a panoramic review. Sol Energy Mater Sol Cells, 2007, 91, 1529 doi: 10.1016/j.solmat.2007.04.031[7] Zhang K H, Xi K, Blamire M G, et al. P-type transparent conducting oxides. J Phys Condens Matter, 2016, 28, 383002 doi: 10.1088/0953-8984/28/38/383002[8] Weiher R, Ley R. Optical properties of indium oxide. J Appl Phys, 1966, 37, 299 doi: 10.1063/1.1707830[9] Erhart P, Klein A, Egdell R G, et al. Band structure of indium oxide: Indirect versus direct band gap. Phys Rev B, 2007, 75, 153205 doi: 10.1103/PhysRevB.75.153205[10] Karazhanov S Z, Ravindran P, Vajeeston P, et al. Phase stability, electronic structure, and optical properties of indium oxide polytypes. Phys Rev B, 2007, 76, 075129 doi: 10.1103/PhysRevB.76.075129[11] Walsh A, Da Silva J L, Wei S H, et al. Nature of the band gap of In2O3 revealed by first-principles calculations and X-ray spectroscopy. Phys Rev Lett, 2008, 100, 167402 doi: 10.1103/PhysRevLett.100.167402[12] Reimann K, Steube M. Experimental determination of the electronic band structure of SnO2. Solid State Commun, 1998, 105, 649 doi: 10.1016/S0038-1098(97)10151-X[13] Fröhlich D, Kenklies R, Helbig R. Band-gap assignment in SnO2 by two-photon spectroscopy. Phys Rev Lett, 1978, 41, 1750 doi: 10.1103/PhysRevLett.41.1750[14] Nagasawa M, Shionoya S. Temperature dependence of the fundamental optical absorption edge in stannic oxide. J Phys Soc Jpn, 1971, 30, 1118 doi: 10.1143/JPSJ.30.1118[15] Schleife A, Varley J, Fuchs F, et al. Tin dioxide from first principles: Quasiparticle electronic states and optical properties. Phys Rev B, 2011, 83, 035116 doi: 10.1103/PhysRevB.83.035116[16] Berger J, Reining L, Sottile F. Efficient GW calculations for SnO2, ZnO, and rubrene: The effective-energy technique. Phys Rev B, 2012, 85, 085126 doi: 10.1103/PhysRevB.85.085126[17] Sabino F P, Oliveira L N, Wei S H, et al. Optical and fundamental band gaps disparity in transparent conducting oxides: new findings for the In2O3 and SnO2 systems. J Phys: Condens Matter, 2017, 29, 085501 doi: 10.1088/1361-648X/aa4e8c[18] Snaith H J, Ducati C. SnO2-based dye-sensitized hybrid solar cells exhibiting near unity absorbed photon-to-electron conversion efficiency. Nano Lett, 2010, 10, 1259 doi: 10.1021/nl903809r[19] Jiang Q, Zhang L, Wang H, et al. Enhanced electron extraction using SnO2 for high-efficiency planar-structure HC(NH2)2PbI3-based perovskite solar cells. Nat Energy, 2017, 2, 16177 doi: 10.1038/nenergy.2016.177[20] Scanlon D O, Dunnill C W, Buckeridge J, et al. Band alignment of rutile and anatase TiO2. Nat Mater, 2013, 12, 798 doi: 10.1038/nmat3697[21] Harrison W A. Elementary theory of heterojunctions. J Vac Sci Technol, 1977, 14, 1016 doi: 10.1116/1.569312[22] Wei S H, Zunger A. Role ofdorbitals in valence-band offsets of common-anion semiconductors. Phys Rev Lett, 1987, 59, 144 doi: 10.1103/PhysRevLett.59.144[23] Wei S H, Zunger A. Calculated natural band offsets of all II–VI and III–V semiconductors: Chemical trends and the role of cation d orbitals. Appl Phys Lett, 1998, 72, 2011 doi: 10.1063/1.121249[24] Walsh A, Da Silva J L F, Wei S H. Multi-component transparent conducting oxides: Progress in materials modelling. J Phys: Condens Matter, 2011, 23, 334210 doi: 10.1088/0953-8984/23/33/334210[25] Chen W, Pasquarello A. Band-edge positions in GW: effects of starting point and self-consistency. Phys Rev B, 2014, 90, 165133 doi: 10.1103/PhysRevB.90.165133[26] Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B, 1999, 59, 1758 doi: 10.1103/PhysRevB.59.1758[27] Heyd J, Scuseria G E, Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J Chem Phys, 2003, 118, 8207 doi: 10.1063/1.1564060[28] Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci, 1996, 6, 15 doi: 10.1016/0927-0256(96)00008-0[29] Haines J, Léger J M. X-ray diffraction study of the phase transitions and structural evolution of tin dioxide at high pressure: Relationships between structure types and implications for other rutile-type dioxides. Phys Rev B, 1997, 55, 11144 doi: 10.1103/PhysRevB.55.11144[30] Landmann M, Rauls E, Schmidt W G. The electronic structure and optical response of rutile, anatase and brookite TiO2. J Phys: Condens Matter, 2012, 24, 195503 doi: 10.1088/0953-8984/24/19/195503[31] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett, 1996, 77, 3865 doi: 10.1103/PhysRevLett.77.3865[32] Aryasetiawan F, Gunnarsson O. The GW method. Rep Prog Phys, 1998, 61, 237 doi: 10.1088/0034-4885/61/3/002[33] Wei S H, Zunger A. Valence band splittings and band offsets of AlN, GaN, and InN. Appl Phys Lett, 1996, 69, 2719 doi: 10.1063/1.117689[34] Kang Y, Kang G, Nahm H H, et al. GW calculations on post-transition-metal oxides. Phys Rev B, 2014, 89[35] Reynolds D C, Look D C, Jogai B, et al. Valence-band ordering in ZnO. Phys Rev B, 1999, 60, 2340 doi: 10.1103/PhysRevB.60.2340[36] Koffyberg F P. Thermoreflectance spectra of CdO: Band gaps and band-population effects. Phys Rev B, 1976, 13, 4470 doi: 10.1103/PhysRevB.13.4470[37] Rebien M, Henrion W, Hong M, et al. Optical properties of gallium oxide thin films. Appl Phys Lett, 2002, 81, 250 doi: 10.1063/1.1491613[38] Trukhin A, Kink M, Maksimov Y, et al. Luminescence of GeO2 glass, rutile-like and α-quartz-like crystals. J Non-Cryst Solids, 2006, 352, 160 doi: 10.1016/j.jnoncrysol.2005.11.027[39] Borgatti F, Berger J A, Céolin D, et al. Revisiting the origin of satellites in core-level photoemission of transparent conducting oxides: The case of n-doped SnO2. Phys Rev B, 2018, 97, 155102 doi: 10.1103/PhysRevB.97.155102 -
Proportional views





 DownLoad:
DownLoad: