| Citation: |
Zheng Zhou, Yixin Li, Zhiyuan Wu, Xinping Ma, Shichang Fan, Shaoyun Huang. The exchange interaction between neighboring quantum dots: physics and applications in quantum information processing[J]. Journal of Semiconductors, 2024, 45(10): 101701. doi: 10.1088/1674-4926/24050043
****
Z Zhou, Y X Li, Z Y Wu, X P Ma, S C Fan, and S Y Huang, The exchange interaction between neighboring quantum dots: physics and applications in quantum information processing[J]. J. Semicond., 2024, 45(10), 101701 doi: 10.1088/1674-4926/24050043
|
The exchange interaction between neighboring quantum dots: physics and applications in quantum information processing
DOI: 10.1088/1674-4926/24050043
CSTR: 32376.14.1674-4926.24050043
More Information-
Abstract
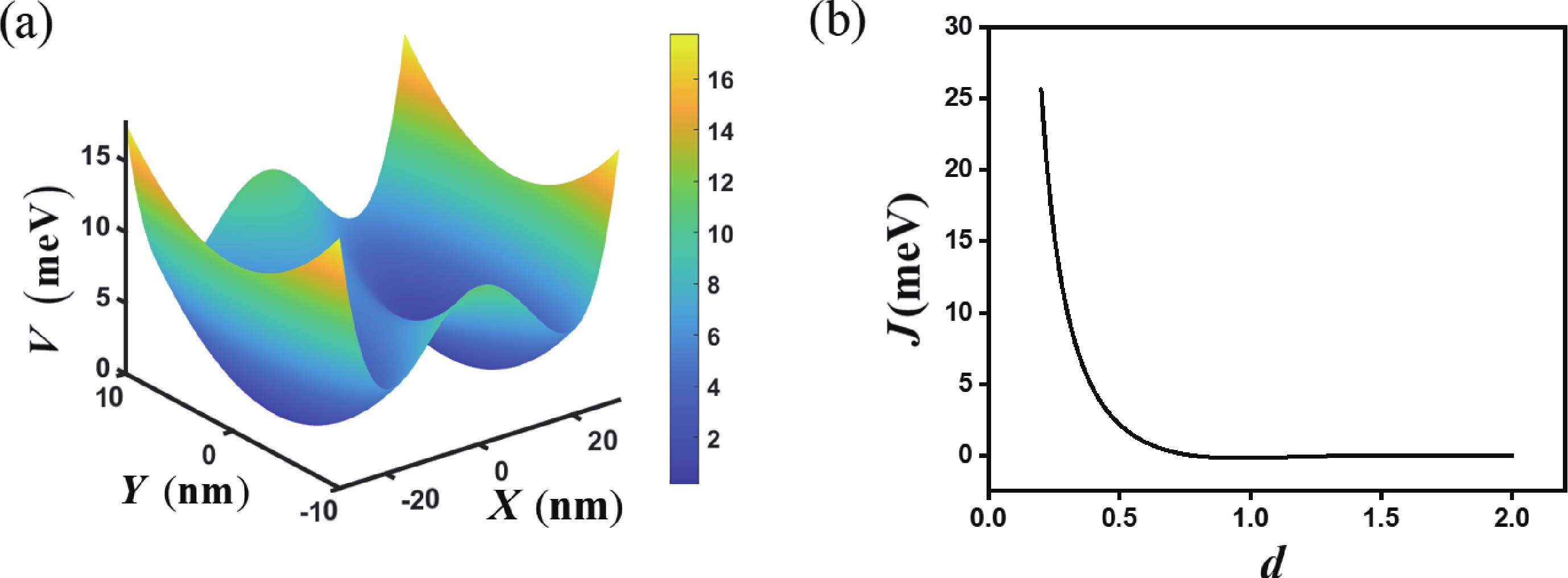
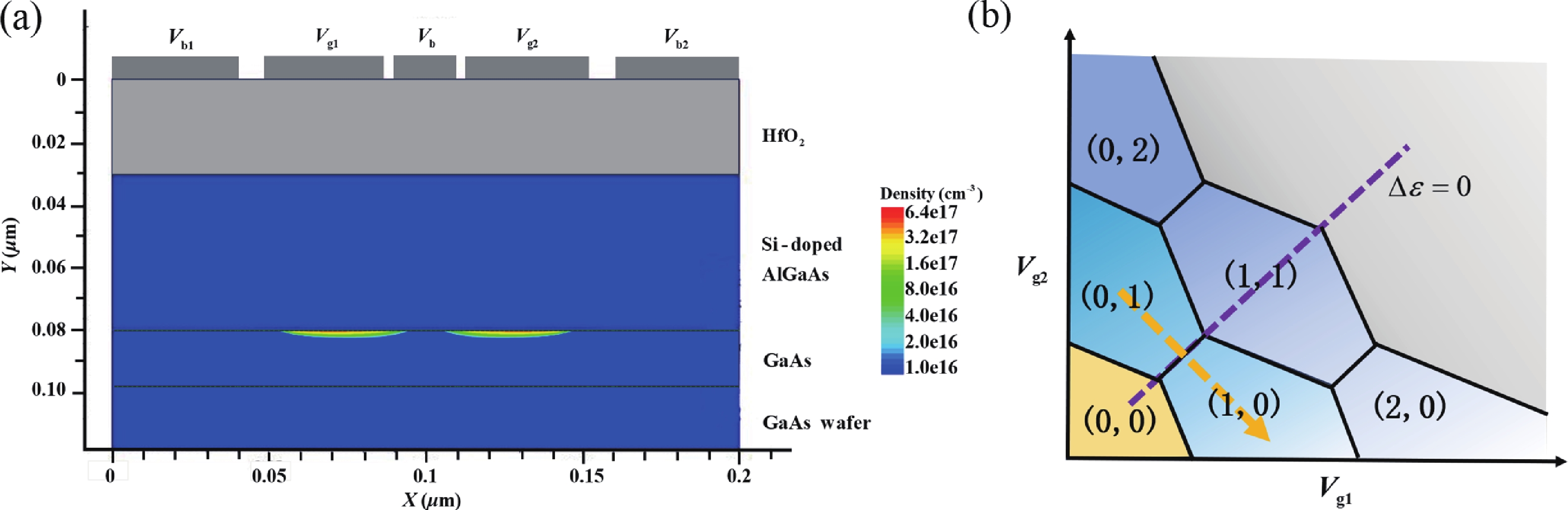
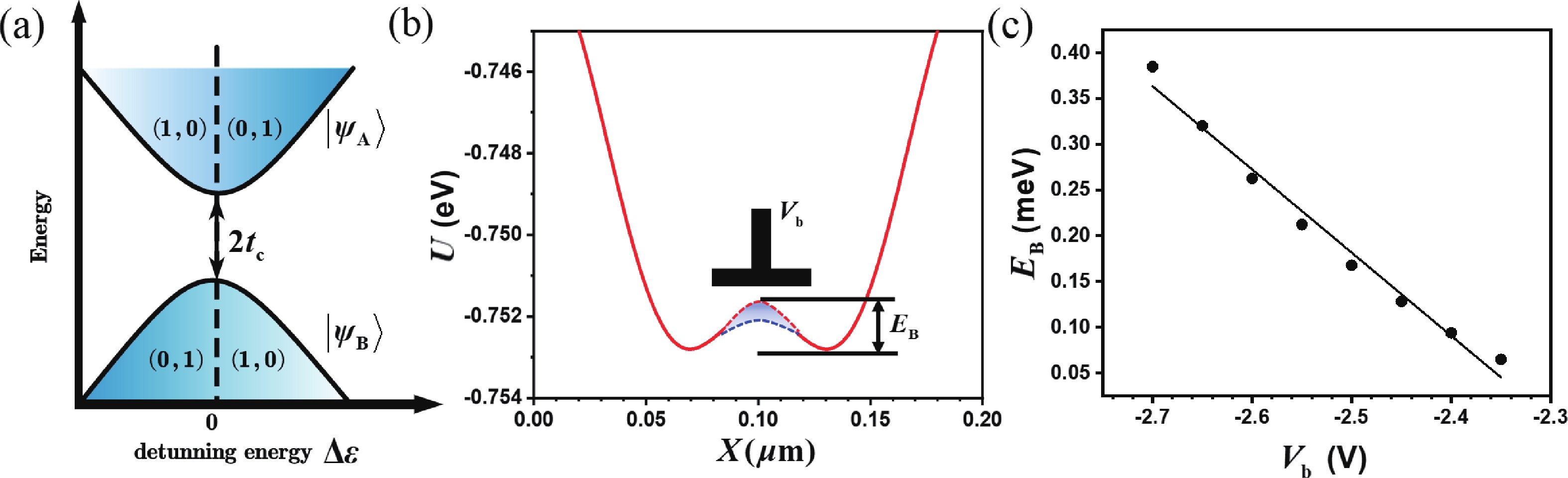
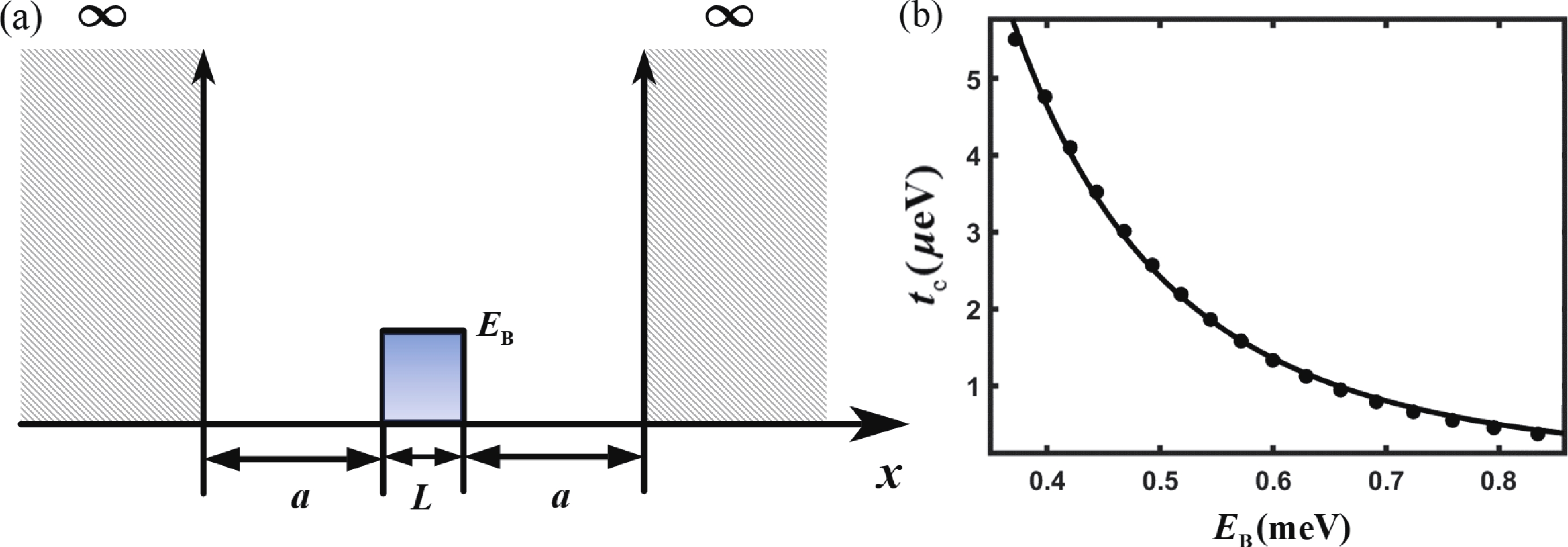
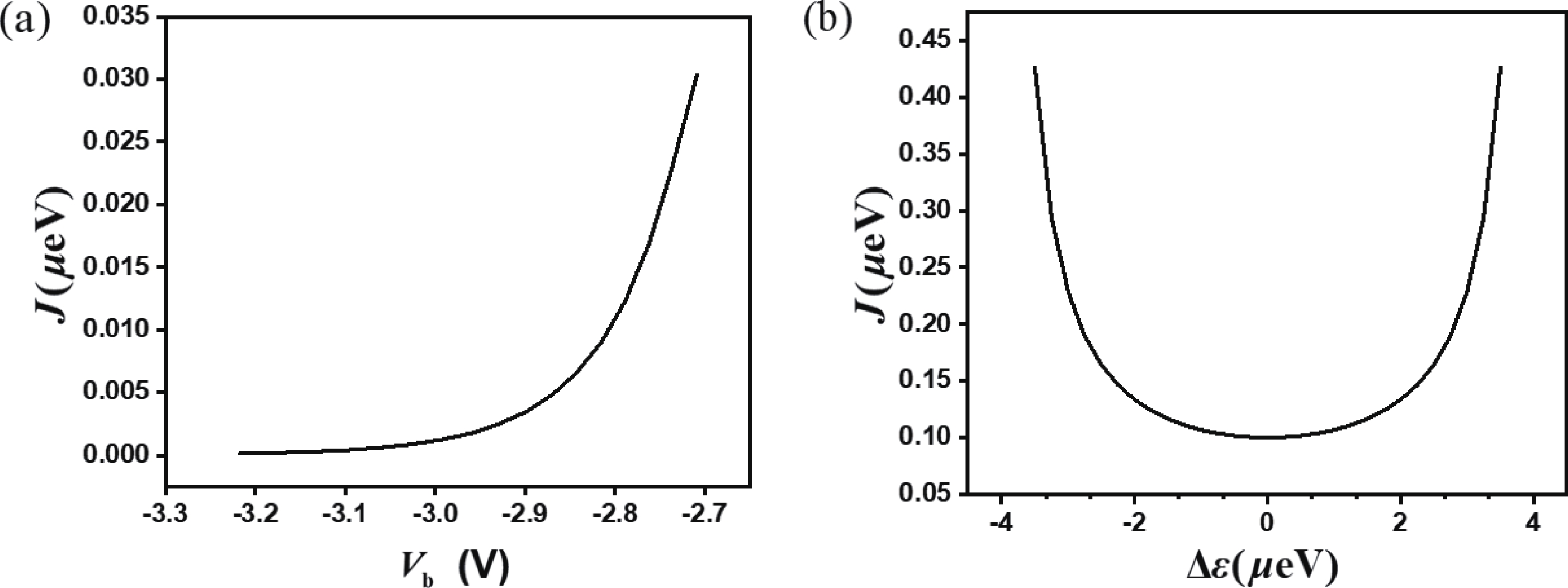
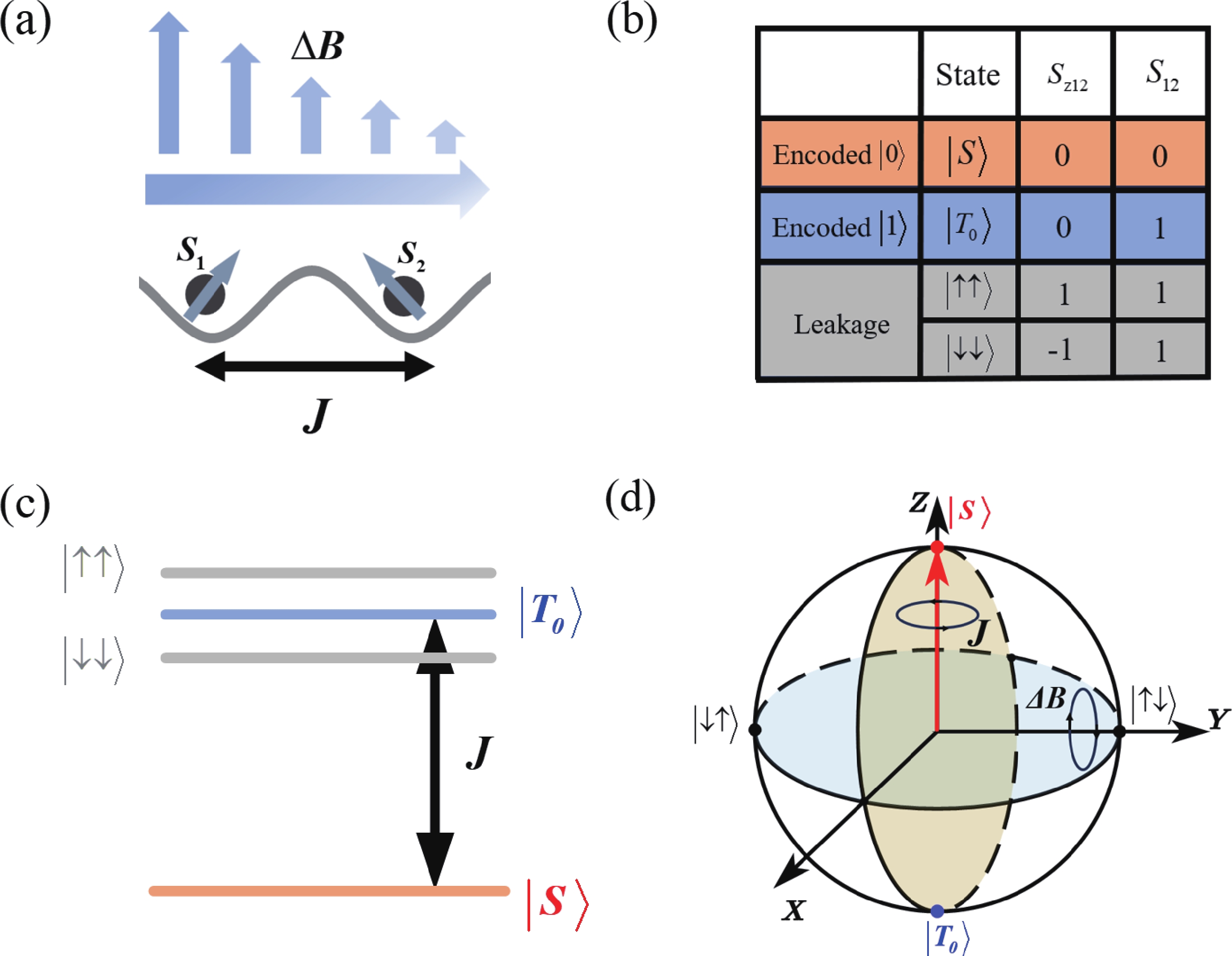
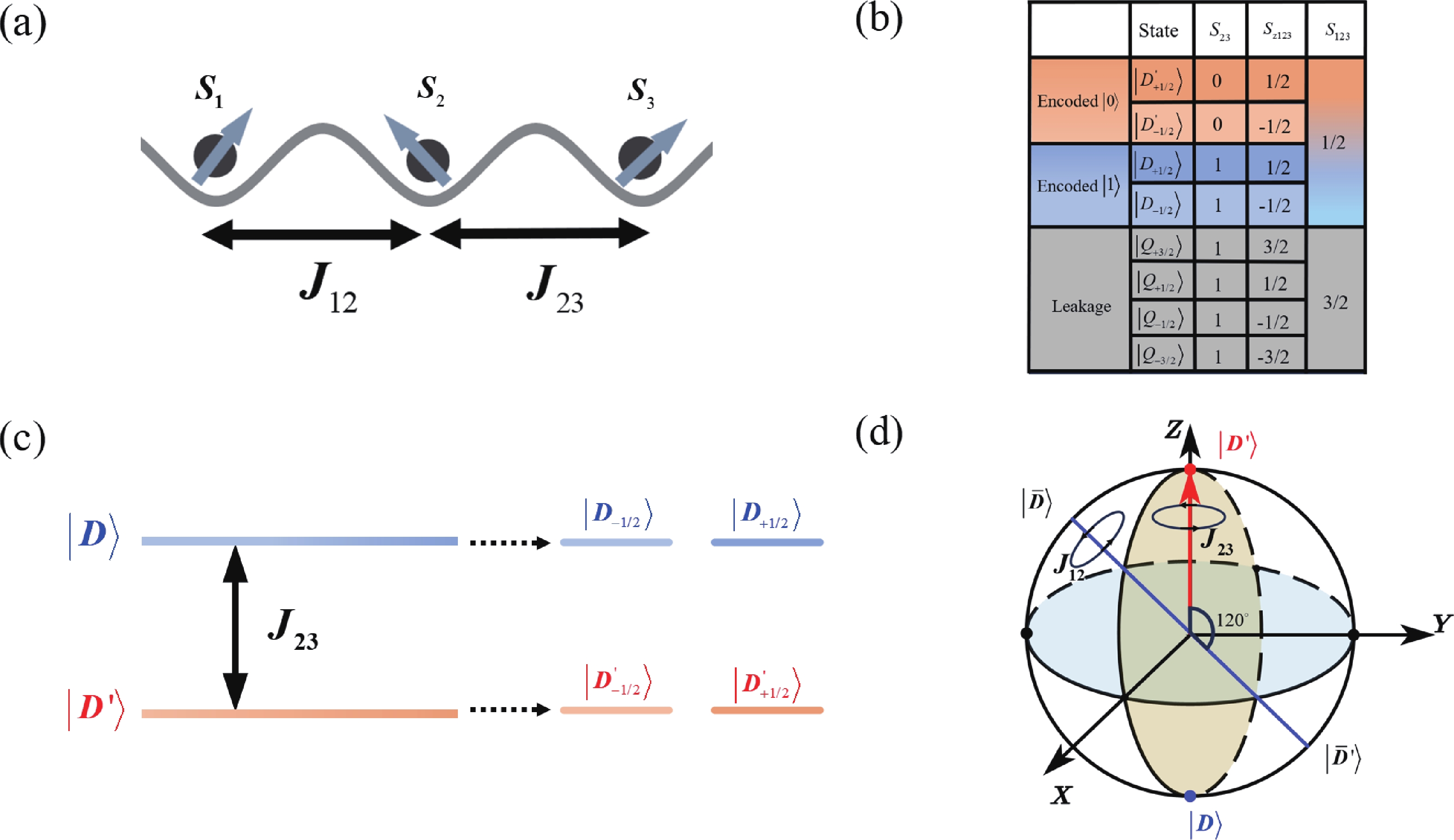
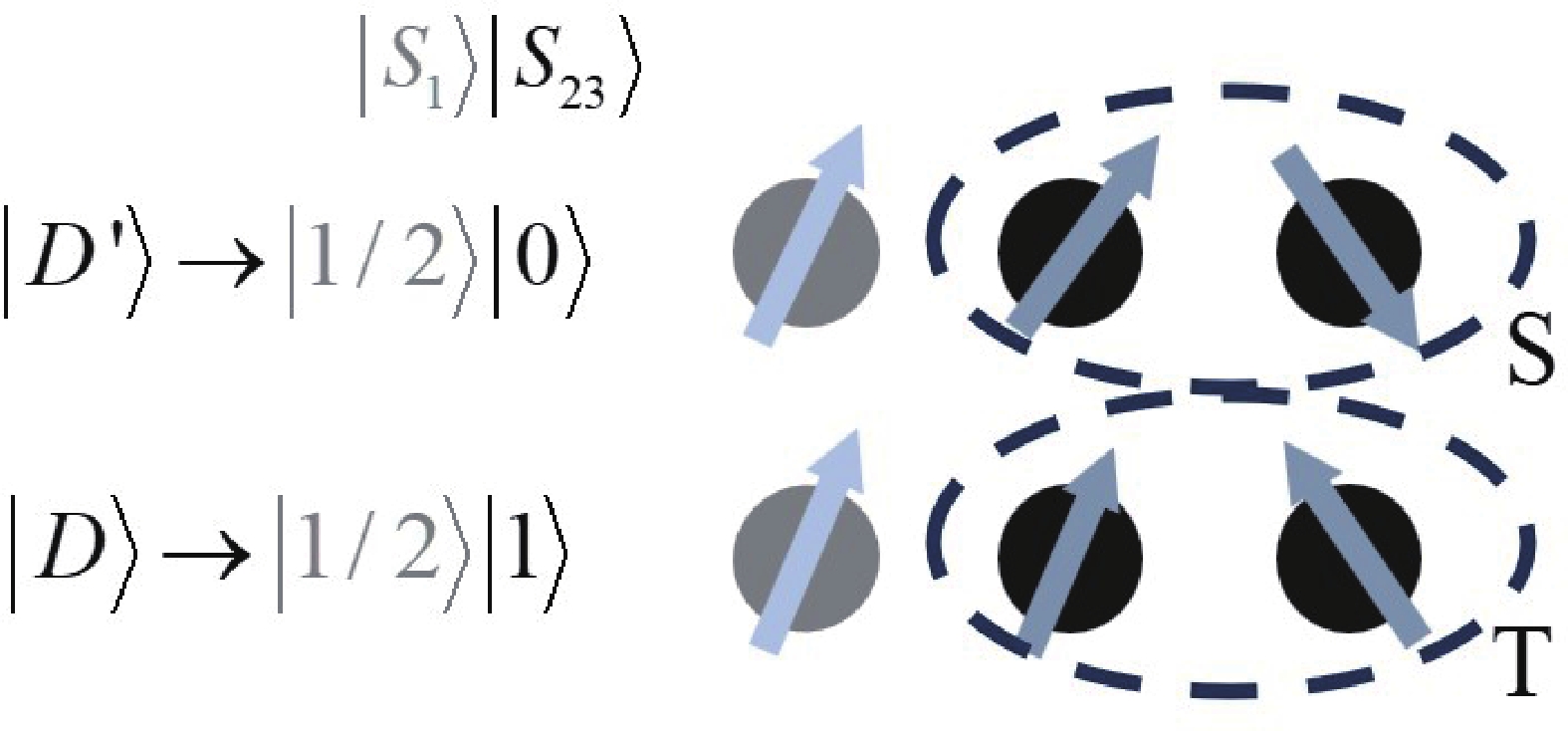
Electron spins confined in semiconductor quantum dots (QDs) are one of potential candidates for physical implementation of scalable quantum information processing technologies. Tunnel coupling based inter exchange interaction between QDs is crucial in achieving single-qubit manipulation, two-qubit gate, quantum communication and quantum simulation. This review first provides a theoretical perspective that surveys a general framework, including the Helter−London approach, the Hund−Mulliken approach, and the Hubbard model, to describe the inter exchange interactions between semiconductor quantum dots. An electrical method to control the inter exchange interaction in a realistic device is proposed as well. Then the significant achievements of inter exchange interaction in manipulating single qubits, achieving two-qubit gates, performing quantum communication and quantum simulation are reviewed. The last part is a summary of this review. -
References
[1] Bhat H A, Khanday F A, Kaushik B K, et al. Quantum computing: fundamentals, implementations and applications. IEEE Open J Nanotechnology, 2022, 3, 61 doi: 10.1109/OJNANO.2022.3178545[2] DiVincenzo D P. The physical implementation of quantum computation. Fortschritte der Physik, 2000, 48(9-11), 771 doi: 10.1002/1521-3978(200009)48:9/11[3] Georgescu I. The DiVincenzo criteria 20 years on. Nat Rev Phys, 2020, 2, 666 doi: 10.1038/s42254-020-00256-4[4] Ladd T, Jelezko F, Laflamme R, et al. Quantum computers. Nature, 2010, 464(4), 45 doi: 10.1038/nature08812[5] Wei S J, Li H, Long G L. A full quantum eigensolver for quantum chemistry simulations. Research, 2020, 1, 111 doi: 10.34133/2020/1486935[6] Shor P W. Algorithms for quantum computation: discrete logarithms and factoring. 35th Annual Symposium on Foundations of Computer Science, 1994, 124 doi: 10.1109/SFCS.1994.365700[7] Grover L K. Quantum mechanics helps in searching for a needle in a haystack. Phys Rev Lett, 1997, 79(2), 325 doi: 10.1103/PhysRevLett.79.325[8] Hanson R, Kouwenhoven L P, Petta J R, et al. Spins in few-electron quantum dots. Rev Mod Phys, 2007, 79(4), 1217 doi: 10.1103/RevModPhys.79.1217[9] Kloeffel C, Loss D. Prospects for spin-based quantum computing in quantum dots. Annu Rev Condens Matter Phys, 2013, 4(1), 51 doi: 10.1146/annurev-conmatphys-030212-184248[10] Zhang X, Li H O, Wang K, et al. Qubits based on semiconductor quantum dots. Chin Phys B, 2018, 27(2), 020305 doi: 10.1088/1674-1056/27/2/020305[11] Chatterjee A, Stevenson P, Franceschi S, et al. Semiconductor qubits in practice. Nat Rev Phys, 2021, 3(3), 157 doi: 10.1038/s42254-021-00283-9[12] Wang N, Wang B C, Guo G P. New progress of silicon-based semiconductor quantum computation. Acta Phys Sin, 2022, 71(23), 230301 doi: 10.7498/aps.71.20221900[13] Zhang X, Li H O, Cao G, et al. Semiconductor quantum computation. Natl Sci Rev, 2019, 6(1), 32 doi: 10.1093/nsr/nwy153[14] Barthelemy P, Vandersypen L M K. Quantum dot systems: a versatile platform for quantum simulations. Ann Phys, 2013, 525(10-11), 808 doi: 10.1002/andp.201300124[15] Burkard G, Ladd T D, Pan A, et al. Semiconductor spin qubits. Rev Mod Phys, 2023, 95(2), 025003 doi: 10.1103/RevModPhys.95.025003[16] Mu J W, Huang S Y, Liu Z H, et al. A highly tunable quadruple quantum dot in a narrow bandgap semiconductor InAs nanowire. Nanoscale, 2021, 13, 3983 doi: 10.1039/D0NR08655J[17] Zwerver A M J, Krähenmann T, Watson T F, et al. Qubits made by advanced semiconductor manufacturing. Nature Electronics, 2022, 5, 184 doi: 10.1038/s41928-022-00727-9[18] Pomorski K, Giounanlis P, Blokhina E, et al. Analytic view on coupled single-electron lines. Semicond Sci Technol, 2019, 34, 125015 doi: 10.1088/1361-6641/ab4f40[19] Lawrie W I L, Eenink H G J, Hendrickx N W, et al. Quantum dot arrays in silicon and germanium. Appl Phys Lett, 2020, 116, 080501 doi: 10.1063/5.0002013[20] Sánchez R, Gallego Marcos F, Platero G. Superexchange blockade in triple quantum dots. Phys Rev B, 2014, 89, 161402(R doi: 10.1103/PhysRevB.89.161402[21] Qiao H, Kandel Y P, Fallahi S, et al. Long-distance superexchange between semiconductor quantum-dot electron spins. Phys Rev Lett, 2021, 126, 017701 doi: 10.1103/PhysRevLett.126.017701[22] Kouwenhoven L P, Austing D G, Tarucha S, et al. Few-electron quantum dots. Rep Prog Phys, 2001, 64, 701 doi: 10.1088/0034-4885/64/6/201[23] Reimann S M, Manninen M. Electronic structure of quantum dots. Rev Mod Phys, 2002, 74, 1283 doi: 10.1103/RevModPhys.74.1283[24] Feng D, Jin G J. Condensed matter physics. Beijing: Higher Education Press, 2013, 1, 1 (in Chinese)[25] Heitler W, London F. Wechselwirkung neutraler atome und homöopolare bindung nach der quantenmechanik. Zeitschrift für Physik, 1927, 44, 455 (in German doi: 10.1007/BF01397394[26] Hatano T, Amaha S, Kubo T, et al. Manipulation of exchange coupling energy in a few-electron double quantum dot. Phys Rev B, 2008, 77(24), 241301 doi: 10.1103/PhysRevB.77.241301[27] Heisenberg V W. Mehrkörperproblem und resonanz in der quantenmechanik. Zeitschrift für Physik, 1926, 38, 411 (in German[28] Dirac P A. On the Theory of quantum mechanics. The Royal society, 1926, 661[29] Mullin W J, Blaylock G. Quantum statistics: Is there an effective fermion repulsion or boson attraction? Am J Phys, 2003, 71, 1223 doi: 10.1119/1.1590658[30] Wannier G H. Statistical physics. New York: Wiley, 1987[31] Leighton R B. Principles of modern physics. New York: McGraw−Hill Book Company, 1959[32] Griffiths D J, Schroeter D F. Introduction to quantum mechanics (third edition). Cambridge: Cambridge university Press, 2018[33] Zeng J Y. Quantum mechanics (fifth edition). Beijing: Science Press, 2013, 1, 1 (in Chinese)[34] Van der Wiel W G, Stopa M, Kodera T, et al. Semiconductor quantum dots for electron spin qubits. New J Phys, 2006, 8, 28 doi: 10.1088/1367-2630/8/2/028[35] Saraiva A L, Calderón M J, Koiller B. Reliability of the Heitler−London approach for the exchange coupling between electrons in semiconductor nanostructures. Phys Rev B, 2007, 233302 doi: 10.1103/PhysRevB.76.233302[36] Liu E K. Semiconductor physics (eighth edition). Beijing: Publishing House of Electronics Industry, 2023 (in Chinese)[37] Burkard G, Loss D, DiVincenzo D P. Coupled quantum dots as quantum gates. Phys Rev B, 1999, 59(3), 2070 doi: 10.1103/PhysRevB.59.2070[38] DiVincenzo D P, Loss D. Quantum information is physical. Superlattices and Microstructures, 1998, 23(3), 420 doi: 10.1006/spmi.1997.0520[39] Fanciulli M. Electron spin resonance and related phenomena in low dimensional structures. Berlin: Springer, 2009[40] Tokura Y, Austing D G, Tarucha S. Single-electron tunnelling in two vertically coupled quantum dots. J Phys Condens Matter, 1999, 11, 6023 doi: 10.1088/0953-8984/11/31/310[41] Laird E A, Taylor J M, DiVincenzo D P, et al. Coherent spin manipulation in an exchange-only qubit. Phys Rev B, 2010, 82, 075403 doi: 10.1103/PhysRevB.82.075403[42] Elzerman J M, Hanson R, Greidanus J S, et al. Few-electron quantum dot circuit with integrated charge read out. Phys Rev B, 2003, 67, 161308(R doi: 10.1103/PhysRevB.67.161308[43] Russ M, Burkard G. Three-electron spin qubits. J Phys Condens Matter, 2017, 29, 393001 doi: 10.1088/1361-648X/aa761f[44] Hubbard J. Electron correlations in narrow energy bands. Proc R Soc Lond A, 1963, 276(1365), 238 doi: 10.1098/rspa.1963.0204[45] Van der Wiel W G, Franceschi S De, Elzerman J M, et al. Electron transport through double quantum dots. Rev Mod Phys, 2003, 75(1), 1 doi: 10.1103/RevModPhys.75.1[46] Spałek J. Theory of unconventional superconductivity in strongly correlated systems: real space pairing and statistically consistent mean-field theory- in perspective. Acta Phys Pol A, 2012, 121(4), 764 doi: 10.12693/APhysPolA.121.764[47] Taylor J M, Petta J R, Johnson A C, et al. Relaxation, dephasing, and quantum control of electron spins in double quantum dots. Phys Rev B, 2007, 76(3), 035315 doi: 10.1103/PhysRevB.76.035315[48] Balachandran A P, Ercolessi E, Morandi G, et al. Hubbard model and anyon superconductivity: a review. Int J Mod Phys B, 1990, 4(14), 2057 doi: 10.1142/S0217979290001030[49] Spałek J. Effect of pair hopping and magnitude of intra-atomic interaction on exchange-mediated superconductivity. Phys Rev B, 1988, 37(1), 533 doi: 10.1103/PhysRevB.37.533[50] Bravyi S, DiVincenzo D P, Loss D. Schrieffer–Wolff transformation for quantum many-body systems. Ann Phys, 2011, 326(10), 2793 doi: 10.1016/j.aop.2011.06.004[51] Assa A. Interacting electrons and quantum magnetism. Berlin: Springer-Verlag, 1998[52] DiCarlo L, Lynch H J, Johnson A C, et al. Differential charge sensing and charge delocalization in a tunable double quantum dot. Phys Rev Lett, 2004, 92(22), 226801 doi: 10.1103/PhysRevLett.92.226801[53] Hu Y J, Churchill H O H, Reilly D J, et al. A Ge/Si heterostructure nanowire-based double quantum dot with integrated charge sensor. Nat Nanotechnol, 2007, 2, 622 doi: 10.1038/nnano.2007.302[54] Wang X M, Huang S Y, Wang J Y, et al. A charge sensor integration to tunable double quantum dots on two neighboring InAs nanowires. Nanoscale, 2021, 13, 1048 doi: 10.1039/D0NR07115C[55] Hsiao T K, van Diepen C J, Mukhopadhyay U, et al. Efficient orthogonal control of tunnel couplings in a quantum dot array. Phys Rev Appl, 2020, 13(5), 054018 doi: 10.1103/PhysRevApplied.13.054018[56] Mills A R, Zajac D M, Gullans M J. et al. Shuttling a single charge across a one-dimensional array of silicon quantum dots. Nat Commun, 2019, 10, 1063 doi: 10.1038/s41467-019-08970-z[57] Hu X D, Sarma S D. Hilbert-space structure of a solid-state quantum computer: two-electron states of a double-quantum-dot artificial molecule. Phys Rev A, 2000, 61(6), 062301 doi: 10.1103/PhysRevA.61.062301[58] Ercan H E, Coppersmith S N, Friesen M. Strong electron−electron interactions in Si/SiGe quantum dots. Phys Rev B, 2021, 104, 235302 doi: 10.1103/PhysRevB.104.235302[59] Bellucci D, Rontani M, Troiani F, et al. Competing mechanisms for singlet−triplet transition in artificial molecules. Phys Rev B, 2004, 69, 201308 doi: 10.1103/PhysRevB.69.201308[60] Giavaras G, Tokura Y. Probing the singlet−triplet splitting in double quantum dots: implications of the ac field amplitude. Phys Rev B, 2019, 100, 195421 doi: 10.1103/PhysRevB.100.195421[61] Stopa M, Marcus C M. Magnetic field control of exchange and noise immunity in double quantum dots. Nano Lett, 2008, 8(6), 1778 doi: 10.1021/nl801282t[62] Geyer S, Hetényi B, Bosco S, et al. Anisotropic exchange interaction of two hole spin qubits. Nat Phys, 2024 doi: 10.1038/s41567-024-02481-5[63] Liu Z H, Entin-Wohlman O, Aharony A, et al. Control of the two-electron exchange interaction in a nanowire double quantum dot. Phys Rev B, 2018, 98, 241303 doi: 10.1103/PhysRevB.98.241303[64] Loss D, DiVincenzo D P. Quantum computation with quantum dots. Phys Rev A, 1998, 57(1), 1050 doi: 10.1103/PhysRevA.57.120[65] Koppens F H L, Buizert C, Tielrooij K J, et al. Driven coherent oscillations of a single electron spin in a quantum dot. Nature, 2006, 442, 766 doi: 10.1038/nature05065[66] Liu H, Wang K, Gao F, et al. Ultrafast and electrically tunable Rabi frequency in a Germanium hut wire hole spin qubit. Nano Lett, 2023, 23(9), 3810 doi: 10.1021/acs.nanolett.3c00213[67] Philips S G J, Mądzik M T, Amitonov S V, et al. Universal control of a six-qubit quantum processor in silicon. Nature, 2022, 609, 919 doi: 10.1038/s41586-022-05117-x[68] Levy J. Universal quantum computation with spin-1/2 pairs and Heisenberg exchange. Phys Rev Lett, 2002, 89, 147902 doi: 10.1103/PhysRevLett.89.147902[69] DiVincenzo D, Bacon D, Kempe J, et al. Universal quantum computation with the exchange interaction. Nature, 2000, 408, 339 doi: 10.1038/35042541[70] Zhang T, Liu H, Cao F, et al. Anisotropic g-factor and spin−orbit field in a germanium hut wire double quantum dot. Nano Lett, 2021, 21(9), 3835 doi: 10.1021/acs.nanolett.1c00263[71] Wang J Y, Huang S Y, Lei Z J, et al. Measurements of the spin−orbit interaction and Landé g factor in a pure-phase InAs nanowire double quantum dot in the Pauli spin-blockade regime. Appl Phys Lett, 2016, 109(5), 053106 doi: 10.1063/1.4960464[72] Petta J R, Johnson A C, Taylor J M, et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science, 2005, 309(5744), 2180 doi: 10.1126/science.1116955[73] Wardrop M P, Doherty A C. Exchange-based two-qubit gate for singlet−triplet qubits. Phys Rev B, 2014, 90, 045418 doi: 10.1103/PhysRevB.90.045418[74] Johnson A C, Petta J R, Taylor J M, et al. Triplet–singlet spin relaxation via nuclei in a double quantum dot. Nature, 2005, 435, 925 doi: 10.1038/nature03815[75] Prance J R, Shi Z, Simmons C B, et al. Single-shot measurement of triplet−singlet relaxation in a Si/SiGe double quantum dot. Phys Rev Lett, 2012, 108, 046808 doi: 10.1103/PhysRevLett.108.046808[76] Weinstein A J, Reed M D, Jones A M, et al. Universal logic with encoded spin qubits in silicon. Nature, 2023, 615, 817 doi: 10.1038/s41586-023-05777-3[77] Andrews R W, Jones C, Reed M D, et al. Quantifying error and leakage in an encoded Si/SiGe triple-dot qubit. Nat Nanotechnol, 2019, 14, 747 doi: 10.1038/s41565-019-0500-4[78] Andrew C D, Matthew P W. Two-qubit gates for resonant exchange qubits. Phys Rev Lett, 2013, 111, 050503. doi: 10.1103/PhysRevLett.111.050503[79] Medford J, Beil J, Taylor J M, et al. Self-consistent measurement and state tomography of an exchange-only spin qubit. Nat Nanotechnol, 2013, 8, 654 doi: 10.1038/nnano.2013.168[80] Petit L, Russ M, Eenink G H G J, et al. Design and integration of single-qubit rotations and two-qubit gates in silicon above one kelvin. Commun Mater, 2022, 3, 82 doi: 10.1038/s43246-022-00304-9[81] Nguyen D Q L, Heinz I, Burkard G. Quantum gates with oscillating exchange interaction. Quantum Science and Technology. 2024, 9, 0150, 20 doi: 10.1088/2058-9565/acef54[82] Sigillito A J, Gullans M J, Edge L F, et al. Coherent transfer of quantum information in a silicon double quantum dot using resonant SWAP gates. npj Quantum Information, 2019, 5, 110 doi: 10.1038/s41534-019-0225-0[83] Zajac D M, Sigillito A J, Russ M, et al. Resonantly driven CNOT gate for electron spins. Science, 2018, 359(6374), 439 doi: 10.1126/science.aao5965[84] Watson T F, Philips S G J, Kawakami E, et al. A programmable two-qubit quantum processor in silicon. Nature, 2018, 555, 633 doi: 10.1038/nature25766[85] Nielsen M A, Chuang I L. Quantum computation and quantum information: 10th Anniversary Edition. Cambridge: Cambridge University Press, 2010[86] Van Riggelen F, Lawrie W I L, Russ M, et al. Phase flip code with semiconductor spin qubits. npj Quantum information, 2022, 8, 12 doi: 10.1038/s41534-022-00517-3[87] Bennett C H, DiVincenzo D P. Quantum information and computation. Nature, 2000, 404, 247 doi: 10.1038/35005001[88] Oh S, Shim Y P, Fei J, et al. Resonant adiabatic passage with three qubits. Phys Rev A, 2013, 87, 022332 doi: 10.1103/PhysRevA.87.022332[89] Gullans M J, Petta J R. Coherent transport of spin by adiabatic passage in quantum dot arrays. Phys Rev B, 2020, 102, 155404 doi: 10.1103/PhysRevB.102.155404[90] Bacon D, Flammia S T. Adiabatic gate teleportation. Phys Rev Lett, 2009, 103, 120504 doi: 10.1103/PhysRevLett.103.120504[91] Bose S. Quantum communication through an unmodulated spin chain. Phys Rev Lett, 2003, 91(20), 207901 doi: 10.1103/PhysRevLett.91.207901[92] Friesen M, Biswas A, Hu X D, et al. Efficient multiqubit entanglement via a spin bus. Phys Rev Lett, 2007, 98, 230503 doi: 10.1103/PhysRevLett.98.230503[93] Kandel Y P, Qiao H, Fallahi S, et al. Coherent spin-state transfer via Heisenberg exchange. Nature, 2019, 573, 553 doi: 10.1038/s41586-019-1566-8[94] Qiao H, Kandel Y P, Manikandan S K. et al. Conditional teleportation of quantum-dot spin states. Nat Commun, 2020, 11, 3022 doi: 10.1038/s41467-020-16745-0[95] Georgescu I M, Ashhab S, Nori F. Quantum simulation. Rev Mod Phys, 2014, 86, 153 doi: 10.1103/RevModPhys.86.153[96] Byrnes T, Kim N Y, Kusudo K, et al. Quantum simulation of Fermi−Hubbard models in semiconductor quantum-dot arrays. Phys Rev B, 2008, 78, 075320 doi: 10.1103/PhysRevB.78.075320[97] Hensgens T, Fujita T, Janssen L, et al. Quantum simulation of a Fermi−Hubbard model using semiconductor quantum dot array. Nature, 2017, 548, 70 doi: 10.1038/nature23022[98] Imada M, Fujimori A, Tokura Y. Metal−insulator transitions. Rev Mod Phys, 70(4), 1039[99] Stafford C A, Sarma S D. Collective Coulomb blockade in an array of quantum dots: a Mott−Hubbard approach. Phys Rev Lett, 1994, 72(22), 3590 doi: 10.1103/PhysRevLett.72.3590[100] Nagaoka Y. Ferromagnetism in a narrow, almost half-filled s band. Phys Rev, 1966, 147, 392 doi: 10.1103/PhysRev.147.392[101] Dehollain J P, Mukhopadhyay U, Michal V P, et al. Nagaoka ferromagnetism observed in a quantum dot plaquette. Nature, 2020, 579, 528 doi: 10.1038/s41586-020-2051-0[102] Maciej L, Anna S, Veronica A, et al. Ultracold atomic gases in optical lattices: mimicking condensed matter physics and beyond. Adv Phys, 2007, 56, 243 doi: 10.1080/00018730701223200[103] Roati G, D’Errico C, Fallani L, et al. Anderson localization of a non-interacting Bose−Einstein condensate. Nature, 2008, 453, 895 doi: 10.1038/nature07071[104] Damski B, Zakrzewski J. Mott-insulator phase of the one-dimensional Bose−Hubbard model: a high-order perturbative study. Phys Rev A, 2006, 74, 043609 doi: 10.1103/PhysRevA.74.043609[105] Wessel S, Alet F, Troyer M, et al. Quantum Monte Carlo simulations of confined bosonic atoms in optical lattices. Phys Rev A, 2004, 70, 053615 doi: 10.1103/PhysRevA.70.053615 -
Supplements
 24050043Supporting_Information.pdf
24050043Supporting_Information.pdf

-
Proportional views





 Zheng Zhou got his B.S. from University of Science and Technology Beijing in 2022. Now he is a master student at Peking University under the supervision of Prof. Shaoyun Huang. His research focuses on quantum computation and semiconductor quantum devices.
Zheng Zhou got his B.S. from University of Science and Technology Beijing in 2022. Now he is a master student at Peking University under the supervision of Prof. Shaoyun Huang. His research focuses on quantum computation and semiconductor quantum devices. Yixin Li got her B.S. from Renmin University of China in 2020. Now she is a PhD student at Peking University under the supervision of Prof. Shaoyun Huang and Prof. Shimin Hou. Her research focuses on quantum transport properties and semiconductor quantum devices.
Yixin Li got her B.S. from Renmin University of China in 2020. Now she is a PhD student at Peking University under the supervision of Prof. Shaoyun Huang and Prof. Shimin Hou. Her research focuses on quantum transport properties and semiconductor quantum devices. Zhiyuan Wu got his B.S. from Hebei University of Technology in 2021. Now he is a Master student at Peking University under the supervision of Prof. Shaoyun Huang. His research focuses on gate defined InAs quantum dot and quantum-classical interface.
Zhiyuan Wu got his B.S. from Hebei University of Technology in 2021. Now he is a Master student at Peking University under the supervision of Prof. Shaoyun Huang. His research focuses on gate defined InAs quantum dot and quantum-classical interface. Xinping Ma got her B.S. from JiLin University in 2022. Now she is a Master student at Peking University under the supervision of Prof. Shaoyun Huang. Her research focuses on Si/SiGe quantum dot and electrical control of Si/SiGe spin qubit.
Xinping Ma got her B.S. from JiLin University in 2022. Now she is a Master student at Peking University under the supervision of Prof. Shaoyun Huang. Her research focuses on Si/SiGe quantum dot and electrical control of Si/SiGe spin qubit. Shichang Fan got his B.S. from East China University of Science and Technology in 2024. Now he is a Master student at Peking University under the supervision of Prof. Shaoyun Huang. His research focuses on the preparation of germanium quantum dots and the theoretical calculation of semiconductor spin qubits.
Shichang Fan got his B.S. from East China University of Science and Technology in 2024. Now he is a Master student at Peking University under the supervision of Prof. Shaoyun Huang. His research focuses on the preparation of germanium quantum dots and the theoretical calculation of semiconductor spin qubits. Shaoyun Huang received B.S. and M.S. degrees in physics from Nanjing University, Nanjing, China, in September 1997 and 2000, respectively, and Ph.D. degree in semiconductor nanoelectronics from Tokyo Institute of Technology in September 2003. He is an associate professor of School of Electronics, Peking University. He is also a key member of the Beijing key laboratory of quantum devices and the Key Laboratory for the Physics and Chemistry of Nanodevices. His research interests include semiconductor quantum dot spin qubits, solid-state quantum computations, semiconductor low dimensional nanostructure based quantum devices, low-temperature transport.
Shaoyun Huang received B.S. and M.S. degrees in physics from Nanjing University, Nanjing, China, in September 1997 and 2000, respectively, and Ph.D. degree in semiconductor nanoelectronics from Tokyo Institute of Technology in September 2003. He is an associate professor of School of Electronics, Peking University. He is also a key member of the Beijing key laboratory of quantum devices and the Key Laboratory for the Physics and Chemistry of Nanodevices. His research interests include semiconductor quantum dot spin qubits, solid-state quantum computations, semiconductor low dimensional nanostructure based quantum devices, low-temperature transport.
 DownLoad:
DownLoad: