| Citation: |
Haitao Li, Jun Qian, Fangfang Han, Tinghui Li. Density functional theory studies of the optical properties of a β-FeSi2 (100)/Si (001) interface at high pressure[J]. Journal of Semiconductors, 2013, 34(7): 072003. doi: 10.1088/1674-4926/34/7/072003
****
H T Li, J Qian, F F Han, T H Li. Density functional theory studies of the optical properties of a β-FeSi2 (100)/Si (001) interface at high pressure[J]. J. Semicond., 2013, 34(7): 072003. doi: 10.1088/1674-4926/34/7/072003.
|
Density functional theory studies of the optical properties of a β-FeSi2 (100)/Si (001) interface at high pressure
DOI: 10.1088/1674-4926/34/7/072003
More Information
-
Abstract
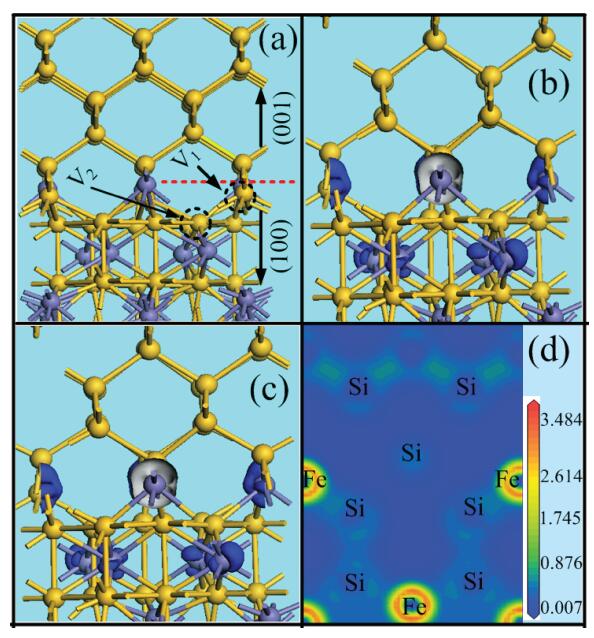
High pressure has a significant influence on β-FeSi2 band gaps and optical absorption tuning. In this work, using density functional theory, we investigate the effect of high pressure on the optical absorption behavior of a β-FeSi2 (100)/Si (001) interface with some Si vacancies. As the pressure increases, the optical absorption peak down-shifts firstly, reach minimum values, and then un-shifts slowly. The electronic orbital analysis indicates that the electronic transition between the highest occupied states and the lowest unoccupied states mainly originate from Fe atoms at the interface regions. Structural analysis discloses that the Si (001) slab partially offsets the pressure exerted on the β-FeSi2 (100) interface, but this effect will become weaker with further increasing pressure, and this physical mechanism plays an important role in its optical absorption behavior. -
References
[1] Noda K, Terai Y, Hasimoto S, et al. Modifications of direct transition energies in β-FeSi2 epitaxial films grown by molecular beam epitaxy. Appl Phys Lett, 2009, 94:241907 doi: 10.1063/1.3155204[2] Yamaguchi K, Mizushima K. Luminescent FeSi2 crystal structure induced by heteroepitaxial stress on Si (111). Phys Rev Lett, 2001, 86:6006 doi: 10.1103/PhysRevLett.86.6006[3] Leong D, Harry M, Reeson K J, et al. A silicon/iron-disilicide light-emitting diode operating at a wavelength of 1.5μm. Nature (London), 1997, 387:686 doi: 10.1038/42667[4] Tani J, Takahashi M, Kido H. Lattice dynamics of β-FeSi2 from first-principles calculations. Phys B, 2010, 405:2200 doi: 10.1016/j.physb.2010.02.008[5] Tassis D H, Mitsas C L, Zorba T T, et al. Infrared spectroscopic and electronic transport properties of polycrystalline semiconducting FeSi2 thin films. J Appl Phys, 1996, 80:962 doi: 10.1063/1.362908[6] Ito M, Nagai H, Oda E, et al. Effects of P doping on the thermoelectric properties of β-FeSi2. J Appl Phys, 2002, 91:2138 doi: 10.1063/1.1436302[7] Ootsuka T, Liu Z X, Osamura M, et al. Studies on aluminum-doped ZnO films for transparent electrode and antireflection coating of β-FeSi2 optoelectronic devices. Thin Solid Films, 2005, 476:30 doi: 10.1016/j.tsf.2004.06.145[8] Makita Y, Nakayama Y, Fukuzawa Y, et al. Important research targets to be explored for β-FeSi2 device making. Thin Solid Films, 2004, 461:202 doi: 10.1016/j.tsf.2004.02.073[9] Xu J X, Yao R H, Liu Y R. Growth of β-FeSi2 thin film on textured silicon substrate for solar cell application. Appl Surf Sci, 2011, 257:10168 doi: 10.1016/j.apsusc.2011.07.011[10] Dalapati G K, Liew S L, Wong A S W, et al. Photovoltaic characteristics of p-β-FeSi2(Al)/n-Si (100) heterojunction solar cells and the effects of interfacial engineering. Appl Phys Lett, 2011, 98:013507 doi: 10.1063/1.3536523[11] Leong D N, Harry M A, Resson K J, et al. On the origin of the 1.5μm luminescence in ion beam synthesized β-FeSi2. Appl Phys Lett, 1996, 68:1649 doi: 10.1063/1.115893[12] Takarabe K, Teranishi R, Oinuma J, et al. Optical properties of β-FeSi2 under pressure. Phys Rev B, 2002, 65:165215 doi: 10.1103/PhysRevB.65.165215[13] Clark S J, Al-Allak H M, Brand S, et al. Structure and electronic properties of FeSi2. Phys Rev B, 1998, 58:10389 doi: 10.1103/PhysRevB.58.10389[14] Miglio L, Meregalli V, Jepsen O. Strain dependent gap nature of epitaxial β-FeSi2 in silicon by first principles calculations. Appl Phys Lett, 1999, 75:385 doi: 10.1063/1.124383[15] Tani J I, Takahashi M, Kido H. First-principles calculations of the structure and elastic properties of β-FeSi2 at high-press. Intermetallics, 2010, 18:1222 doi: 10.1016/j.intermet.2010.03.023[16] Miki T, Matsui Y, Teraoka Y, et al. Point defects and thermoelectric properties of iron disilicide ceramics sintered with SiH4-plasma-processed micrograins. J Appl Phys, 1994, 76:2097 doi: 10.1063/1.357620[17] Liu Z X, Tanaka M, Kuroda R, et al. Influence of Si/Fe ratio in multilayer structures on crystalline growth of β-FeSi2 thin film on Si substrate. Appl Phys Lett, 2008, 93:021907 doi: 10.1063/1.2957990[18] Hamann D R, Schluter M, Chiang C. Norm-conserving pseudopotentials. Phys Rev Lett, 1979, 43:1494 doi: 10.1103/PhysRevLett.43.1494[19] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett, 1996, 77:3865 doi: 10.1103/PhysRevLett.77.3865[20] Liu L Z, W. Xu, Wu X L, et al. Electronic states and photoluminescence of TiO2 nanotubes with adsorbed surface oxygen. Appl Phys Lett, 2012, 100:121904 doi: 10.1063/1.3695167[21] Liu L Z, Wu X L, Liu X X, et al. Electronic structure and optical properties of β-FeSi2 (100)/Si (001) interface at high pressure. Appl Phys Lett, 2012, 101:111909 doi: 10.1063/1.4752154 -
Proportional views





 DownLoad:
DownLoad:
















