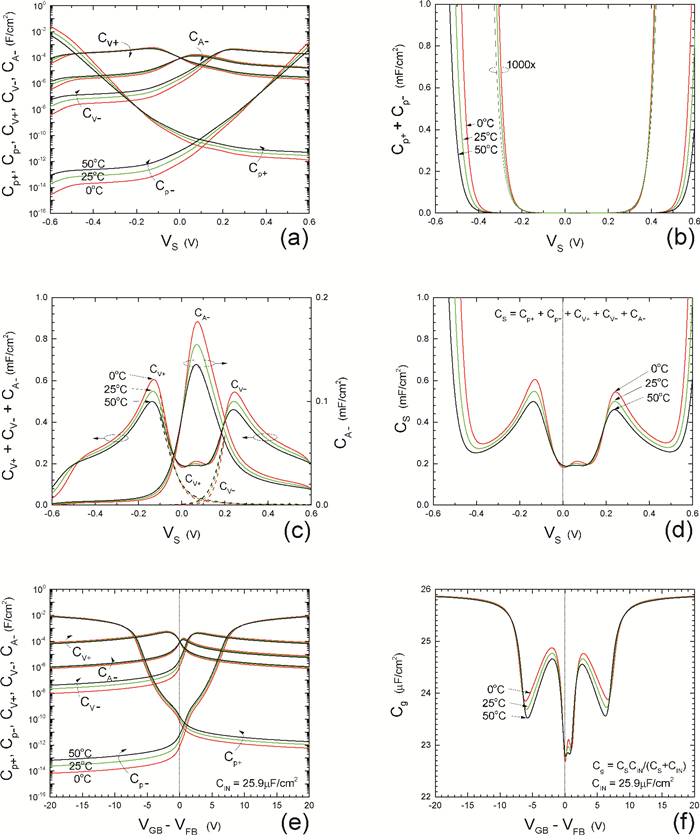
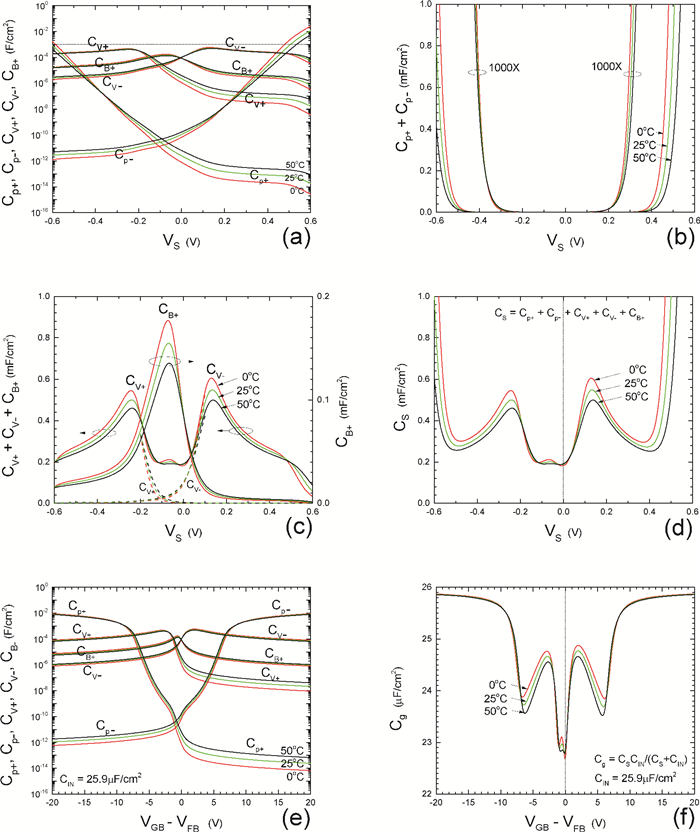
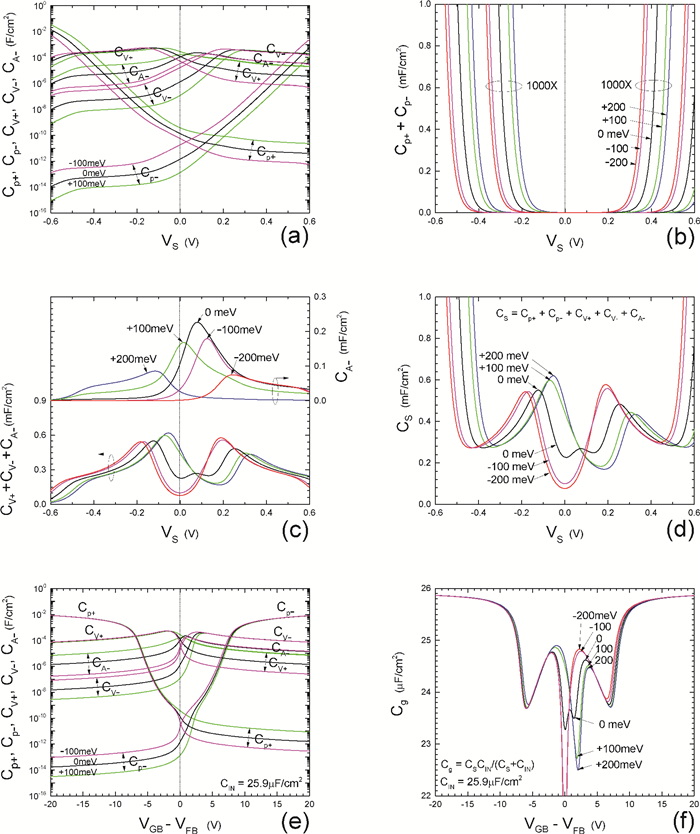
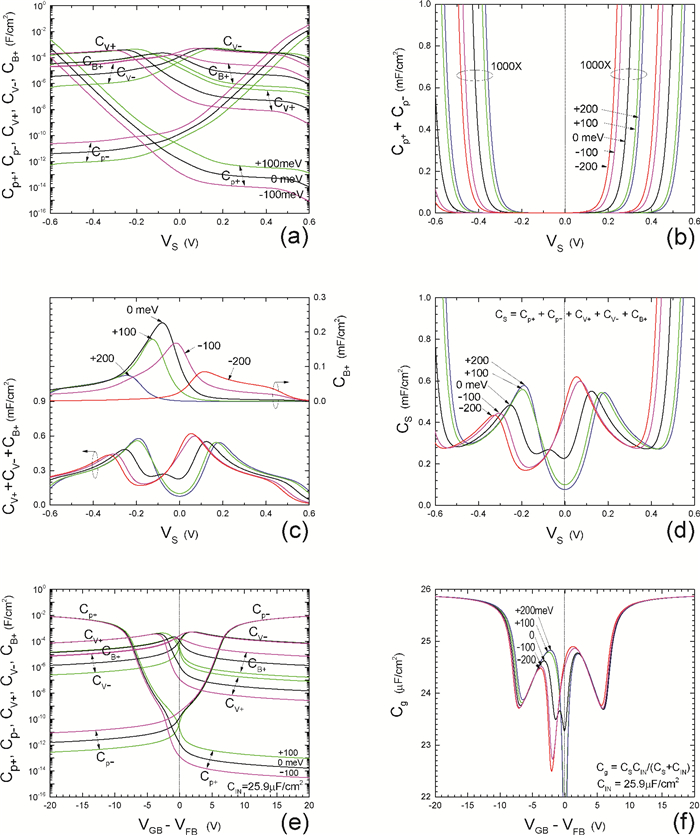
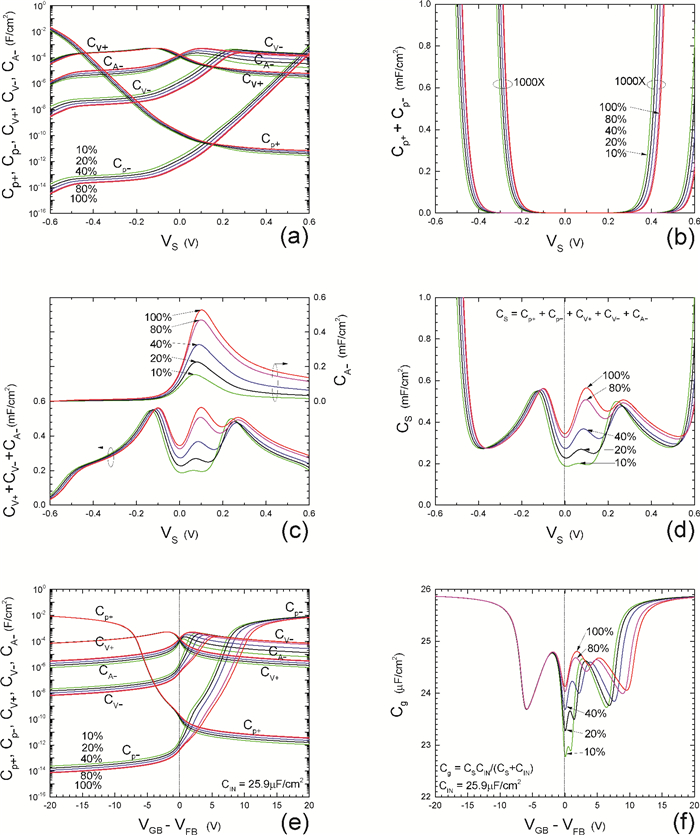
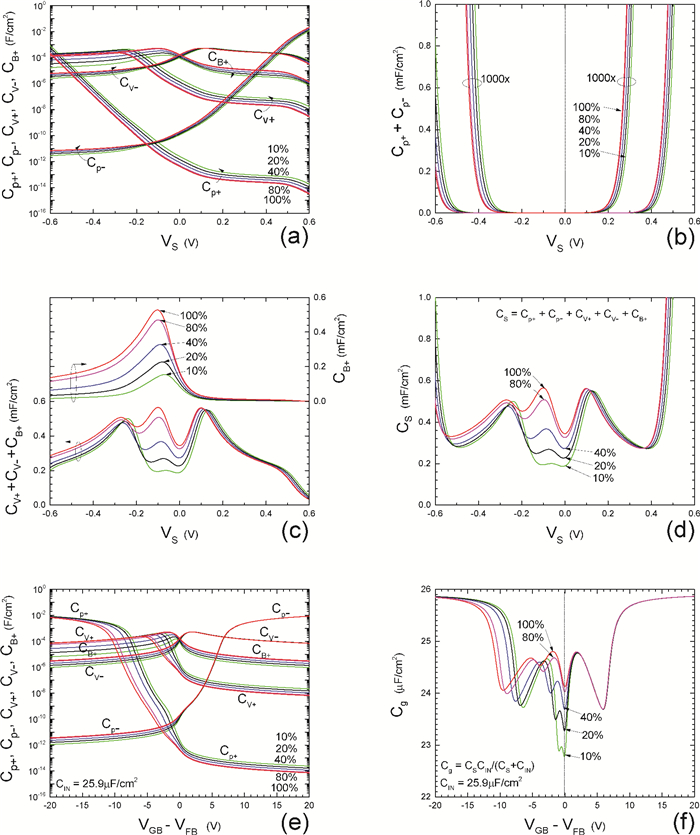
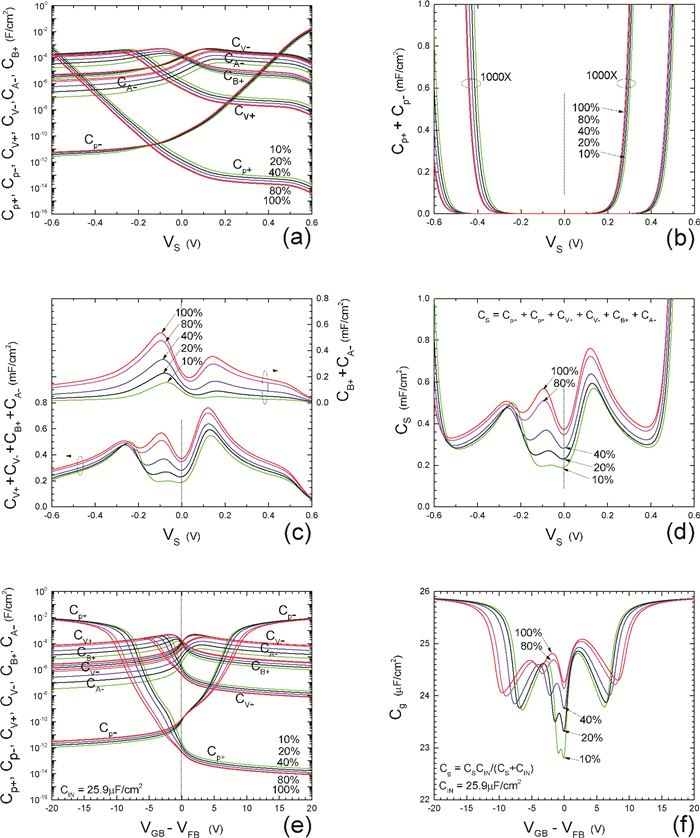
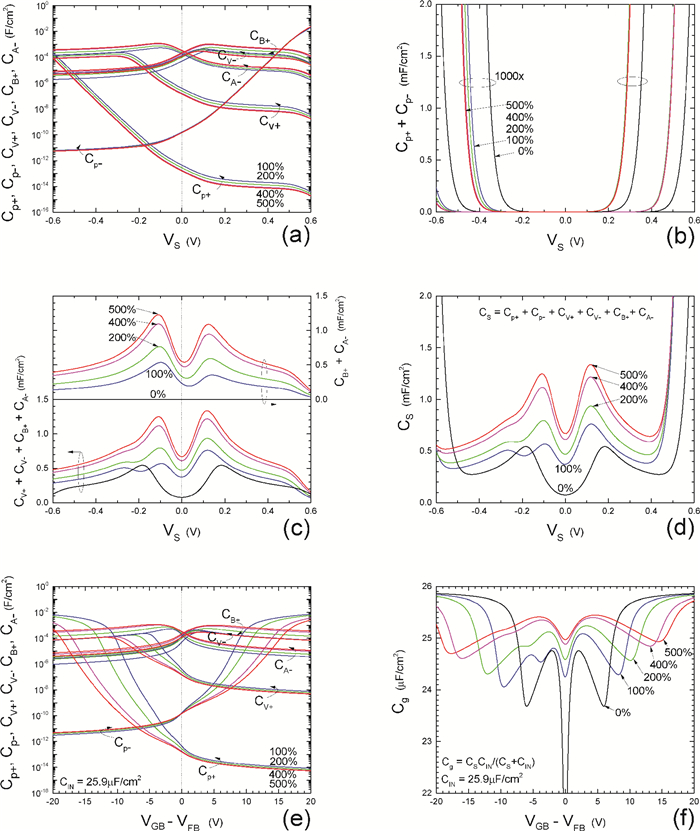
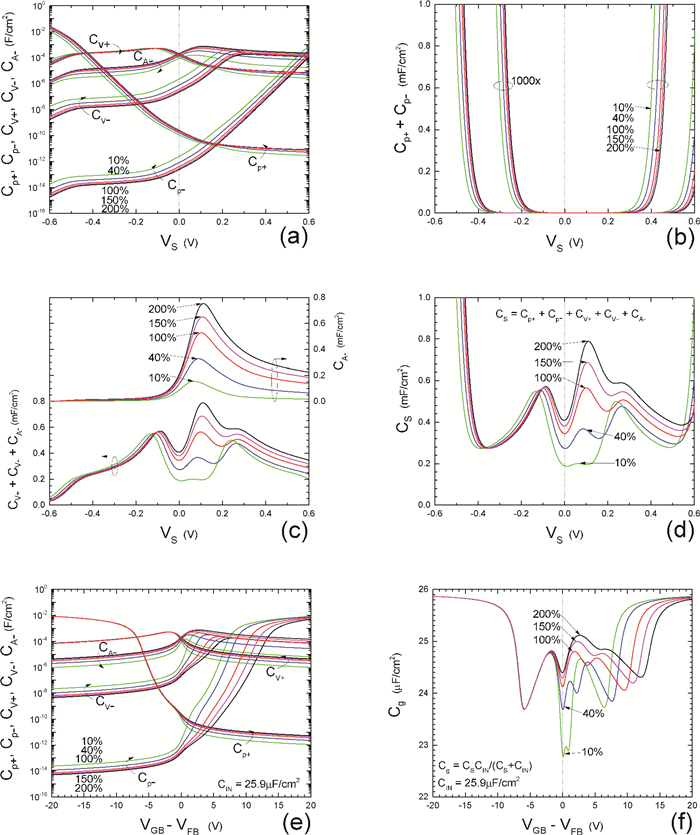
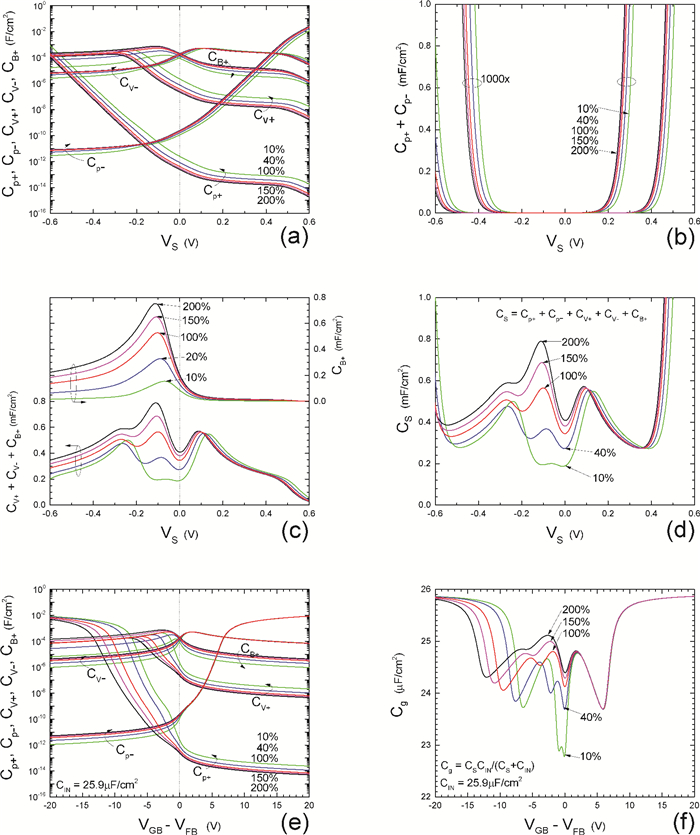
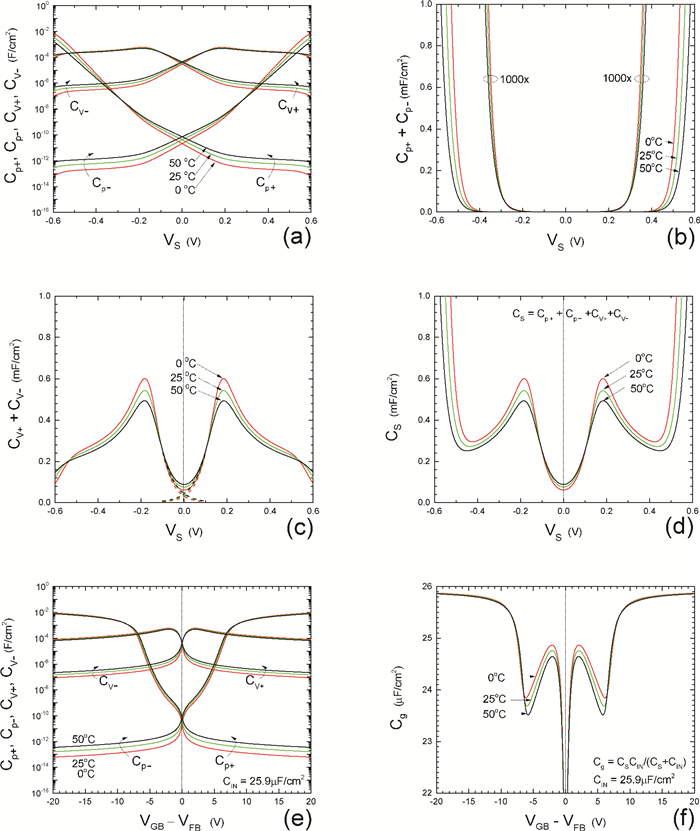
Insulator capacitance CIN = large. (a) Mobile proton storage capacitances, Cp+ and Cp-, trapped proton storage capacitances, CV+, CV- and trapping-limited mobile impurity ion storage capacitance CB+ as a function of surface potential VS at the water surface. (b) Total mobile proton storage capacitance Cp+ + Cp- versus VS. (c) CV+ + CV-+CB+ versus VS. (d) Water capacitance CS versus VS.
Insulator capacitance CIN = 25.9 μF/cm2. (e) Cp+, Cp-, CV+, CV- and CB+, as a function of the DC voltage applied to the metal gate relative to the body, VGB, shifted by the flatband voltage VFB (VS = 0). (f) Gate capacitance Cg versus VGB-VFB.
Notice the symmetry of all curves with respect to the flatband. This is expected from the identical experimental trapping energy, 128 meV, determined by few data, of the positive and negative conduction protons of the amphoteric protonic water. Such closeness is also anticipated from the neutral proton trap of the positive and negative protons.
| Citation: |
Binbin Jie, Chihtang Sah. Solid State Physics View of Liquid State Chemistry Ⅱ. Electrical Capacitance of Pure and Impure Water[J]. Journal of Semiconductors, 2014, 35(2): 021001. doi: 10.1088/1674-4926/35/2/021001
****
B B Jie, C T Sah. Solid State Physics View of Liquid State Chemistry Ⅱ. Electrical Capacitance of Pure and Impure Water. J. Semicond., 2014, 35(2): 021001. doi: 10.1088/1674-4926/35/2/021001.
|
Solid State Physics View of Liquid State Chemistry Ⅱ. Electrical Capacitance of Pure and Impure Water
DOI: 10.1088/1674-4926/35/2/021001
More Information
-
Abstract
More than 80 years of theories and experiments on water suggested to us, described in our first water-physics report, that pure water's "abnormally" high electrical conductivity is due to transport of positive and negative quasi-protons, p+ and p-, between the neutral proton traps V0 ≡ (H2O)0 in the extended water, [(H2O)N→∞]0±, converting it respectively to positively and negatively charged proton traps, V+ ≡ (H3O)1+ and V- ≡ (HO)1-. In this second report, we present the theoretical charge control capacitances of pure and impure water as a function of the DC electric potential applied to water. -
References
[1] Sah Chihtang and Jie Binbin, "Semiconductor Physics View of Liquid State Chemistry, " Invited Paper at the Special Session, the Sah Pen-Tung 111th Anniversary Symposium, of the 2013 National Fall-Meeting of the Chinese Physical Society, August 13-15, 2013, Xiamen University, Xiamen, Fujian, China.[2] Jie Binbin and Sah Chihtang, "Solid State Physics View of Liquid State Chemistry-Electrical conduction in pure water, " Journal of Semiconductors 34(12) 121001-121001-8, December 2013.[3] J. D. Bernal and R. H. Fowler (Cambridge), "A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions, " J. Chem. Phys. 1(8), 515-548, August, 1933. Received April 29, 1933. (University of Cambridge, England. )[4] Linus Pauling (Caltech), "The structure and entropy of ice and other crystals with some randomness of atomic arrangement, " J. Amer. Chem. Soc. 57(12), 2680-2684, December 1935. Received September 24, 1935. (Gates Chemical Laboratory, Caltech, Pasadena. )[5] W. F. Giauque and H. L. Hohnston (UC Berkeley), "Symmetrical and Antisymmetrical Hydrogen and the Third Law of Thermodynamics. Thermal Equilibrium and the Triple Point Pressure", J. Amer. Chem. Soc. 50, 3221-3228, 1928; J. O. Clayton and W. F. Giauque, "The Heat Capacity and Entropy of Carbon Monoxide. Heat of Vaporation. Vapor Pressures of Solid and Liquid. Free Energy To 5000°K. From Spectroscopic Data", J. Amer. Chem. Soc. 54, 2610-2626, 1932; W. W. Blue and W. F. Giauque, "The Heat Capacity and Vapor Pressure of Solid and Liquid Nitrous Oxide. The Entropy from its Band Spectrum", J. Amer. Chem. Soc. 57, 991-997, 1935. Quoted by Pauling in [2].[6] N. H. Fletcher (University of New England University), The Chemical Physics of Ice (Cambridge Monographs on Physics), Cambridge University Press. 1970. Digital version 2009. Made in the U. S. A. Lexington, KY, 03 September 2013. 271pp.[7] N. H. Fletcher, "Structural aspects of the ice-water system, " Report Progress Physics, 34, 913-994, 1971.[8] Peter V. Hobbs (University of Washington, Seattle), Ice Physics, Oxford Classic Texts in the Physical Sciences, Oxford University Press, Oxford, 1974. Paperback 2010. 837 pp. A detailed description of the Pauling's zero-point entropy calculation[4] for the 1h hexagonal ice crystal is given in section 1. 2. 2 on p. 25-33, including the 1964 analytical solution of Hollins that took into account of the correlated motion of the smallest hexagonal ring structure containing the six H2O molecules ring, and the interference between rings described by DiMarzio and Sillinger in 1964 which was extended by Nagle in 1966 giving S0=Rloge[(3/2)×(1+1/729)2+0. 002732]=3. 4103 J/mol-degree almost in exact agreement with the experimental value of 3. 41, obtained from constant pressure heat capacity measurements made by Giauque and Stout in 1936, and lower temperature measurement in 1960 made by Simon, and further extended to nearly 0°K in 1966 by Flubacher and co-authors, giving a residual experimental value of 3. 41 calculated by Eisenberg and Kauzmann in 1969, as indicated in Fig. 5. 7 on p 363 and Table 5. 4 on p. 364. These ascertained the position of the two protons in the 1h hexagonal ice, which is more than 70% of ice.[9] Chih-Tang Sah and William Shockley, "Electron-hole recombination statistics in semiconductors through flaws with many charge conditions, " Physical Review, v109, 1103-1115, 15 February 1958[10] Chih-Tang Sah, "The equivalent circuit model in solid-state electronics, I. The single level defect centers, " Proc. IEEE, v55, 654-672, May 1967. "The equivalent circuit model in solid-state electronics, Ⅱ. The multiple level impurity centers, " Proc. IEEE, v55, 673-685, May 1967. "The equivalent circuit model in solid-state electronics, Ⅲ. Conduction and displacement currents, " Solid-State Electronics, v13, 1547-1575, December 1970. "Equivalent circuit models in semiconductor transport for thermal, optical, Auger-impact and tunneling recombination-generation-trapping processes, " Physica Status Solidi, (a)v7, 541-559, 16 October 1971.[11] Jie Binbin and Sah Chihtang, "MOS Capacitance-Voltage Characteristics from Electron-Trapping at Dopant Donor Impurity," Journal of Semiconductors, 32(4), 041001-1-9, April 2011. "MOS Capacitance-Voltage Characteristics: Ⅱ. Sensitivity of Electronic Trapping at Dopant Impurity from Parameter Variations," Journal of Semiconductors, 32(12), 121001-1-11, December 2011. "MOS Capacitance-Voltage Characteristics: Ⅲ. Trapping Capacitance from 2-Charge-State Impurities," Journal of Semiconductors, 32(12), 121002-1-16, December 2011. "MOS Capacitance-Voltage Characteristics: IV. Trapping Capacitance from 3-Charge-State Impurities," Journal of Semiconductors, 33(1), 011001-1-19, January 2012. "MOS Capacitance-Voltage Characteristics: V. Methods to Enhance the Trapping Capacitance," Journal of Semiconductors, 33(2), 011001-1-19, February 2012.[12] William L. Marshall and E. U. Franck, "Ion Product of Water Substance, 0-1000C, 1-10000 bars - New International Formulation and Its Background", J. Phys. Chem. Ref. Data, vol. 10, No. 2, pp. 295-304, 1981. -
Proportional views





 DownLoad:
DownLoad: