| Citation: |
N. Nouri, G. Rashedi. Band structure of monolayer of graphene, silicene and silicon-carbide including a lattice of empty or filled holes[J]. Journal of Semiconductors, 2018, 39(8): 083001. doi: 10.1088/1674-4926/39/8/083001
****
N. Nouri, G. Rashedi, Band structure of monolayer of graphene, silicene and silicon-carbide including a lattice of empty or filled holes[J]. J. Semicond., 2018, 39(8): 083001. doi: 10.1088/1674-4926/39/8/083001.
|
Band structure of monolayer of graphene, silicene and silicon-carbide including a lattice of empty or filled holes
DOI: 10.1088/1674-4926/39/8/083001
More Information
-
Abstract
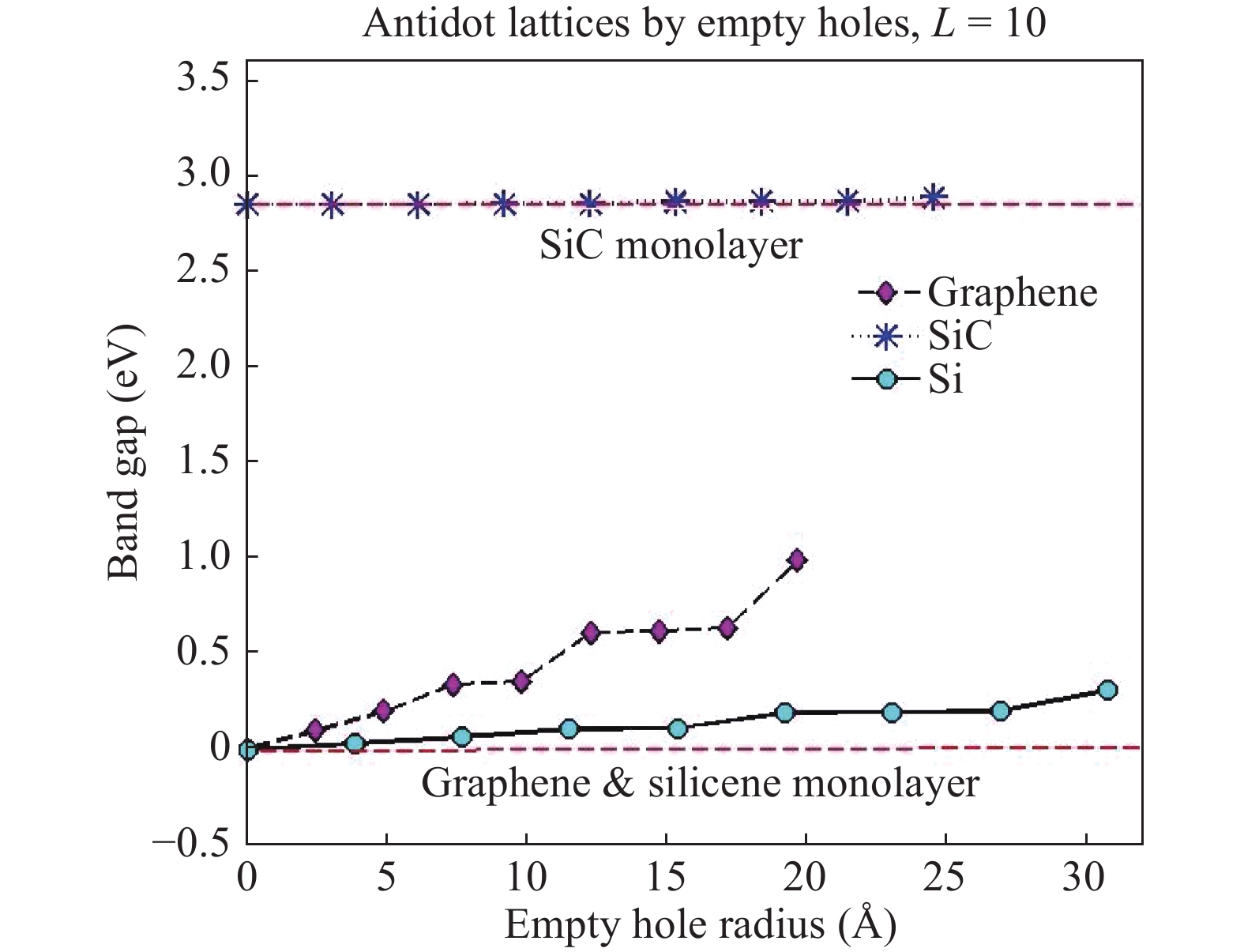
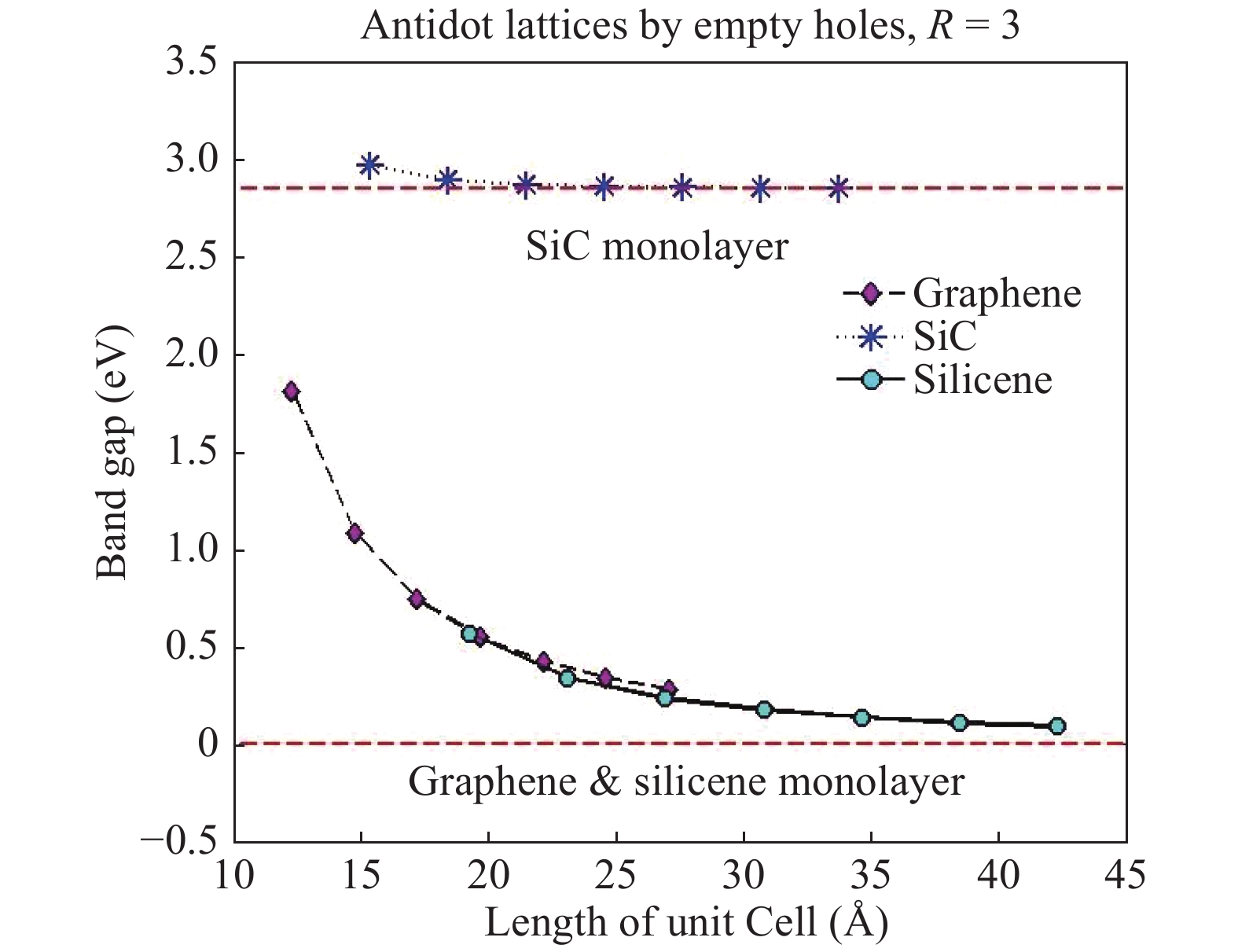
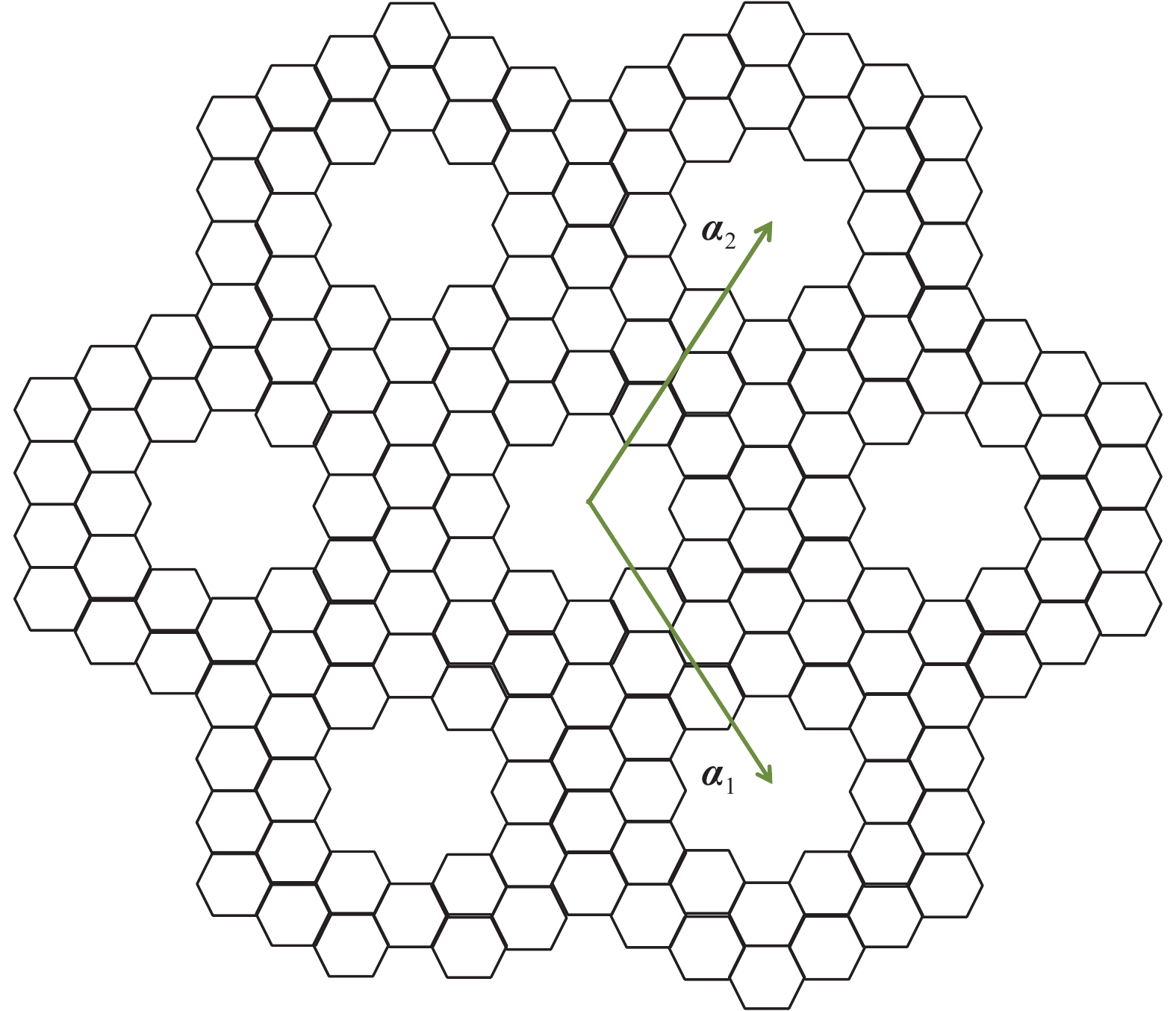
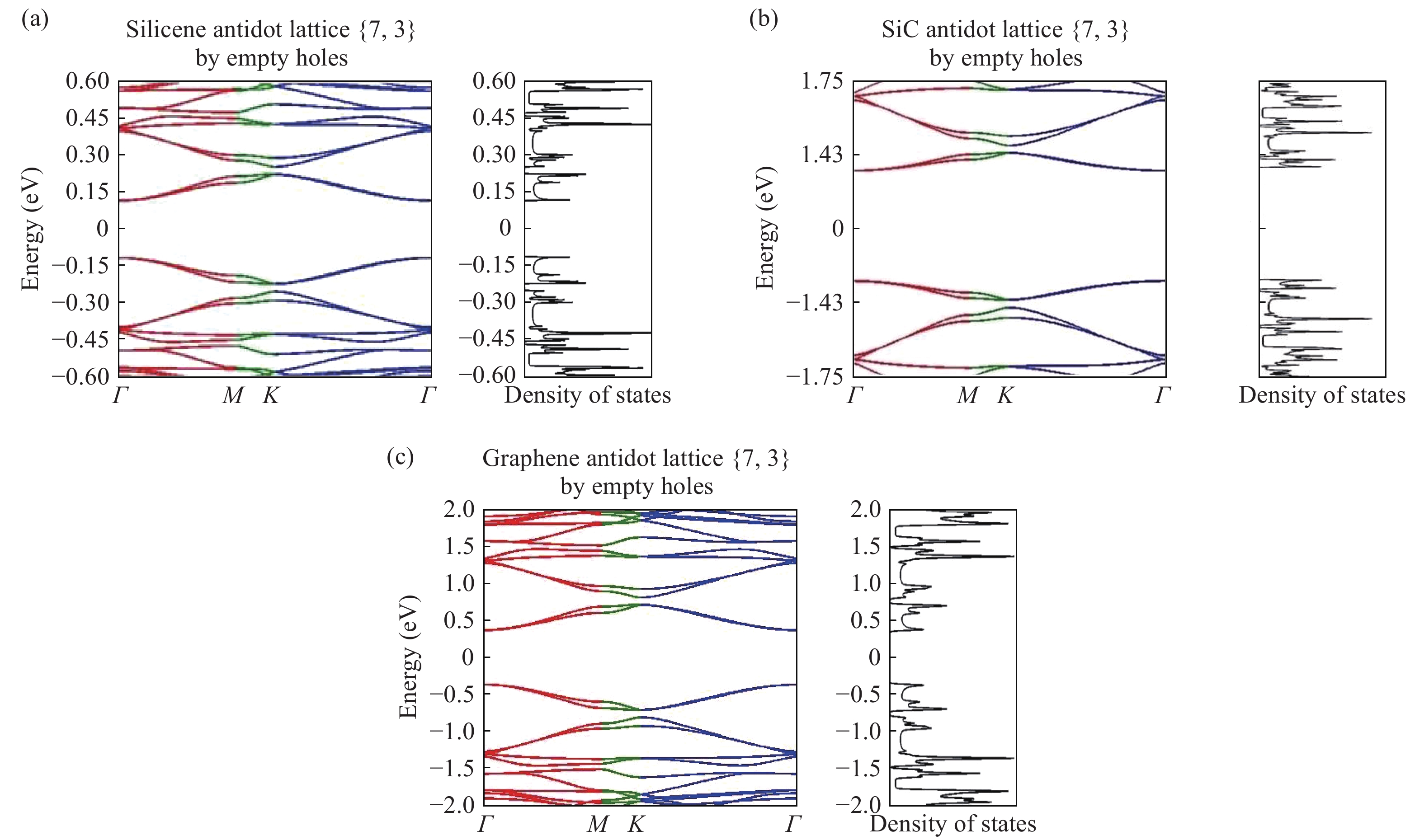
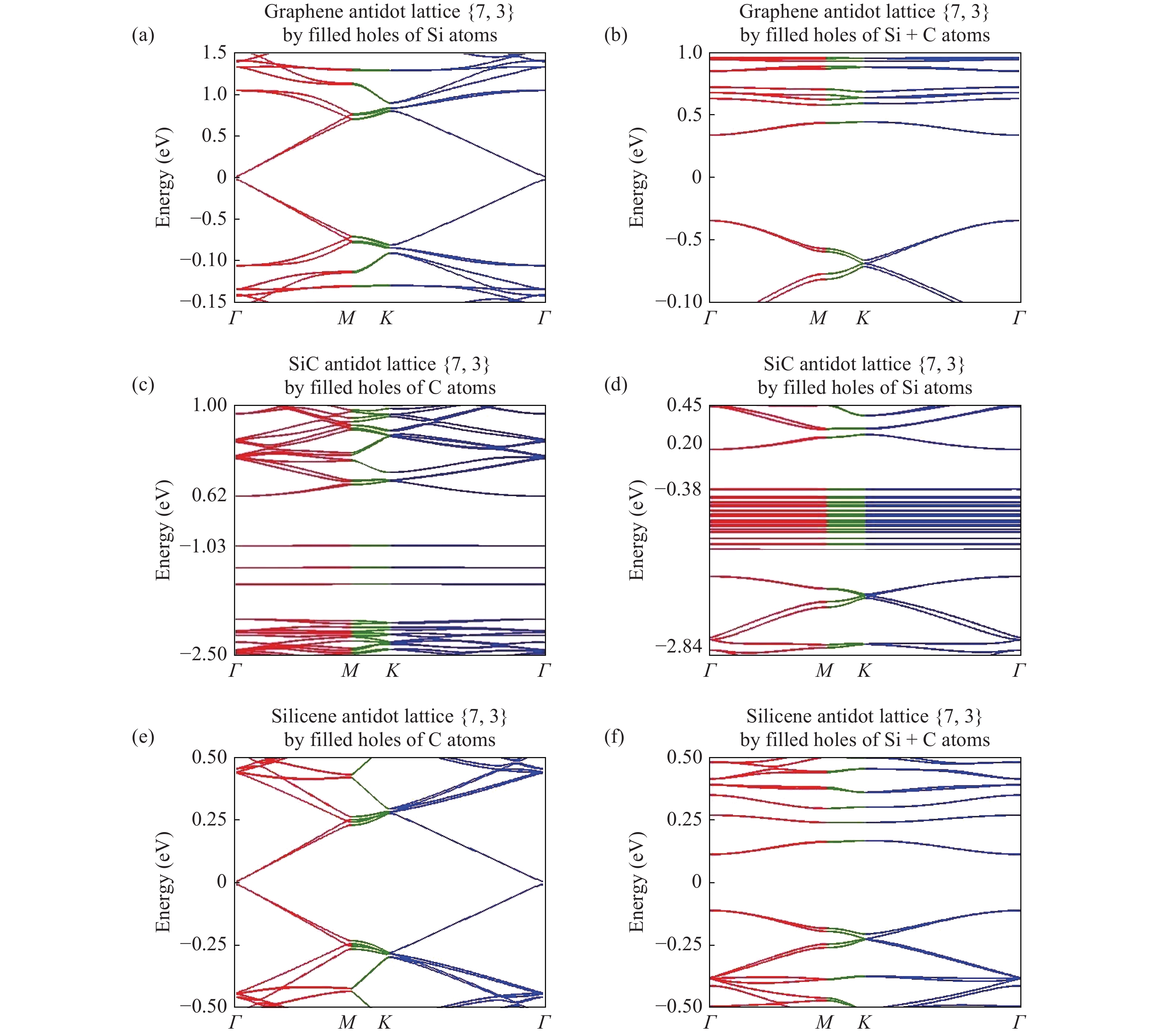
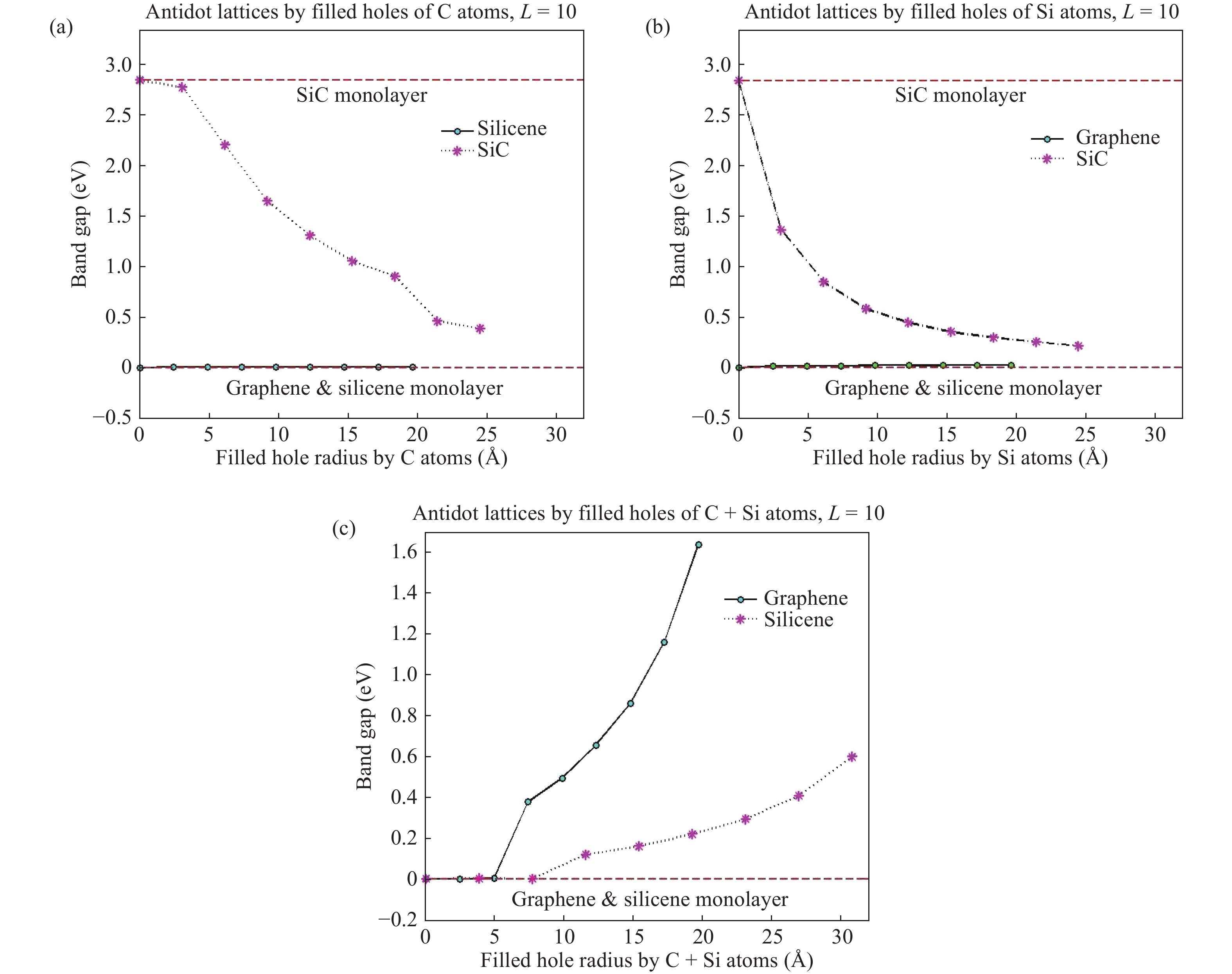
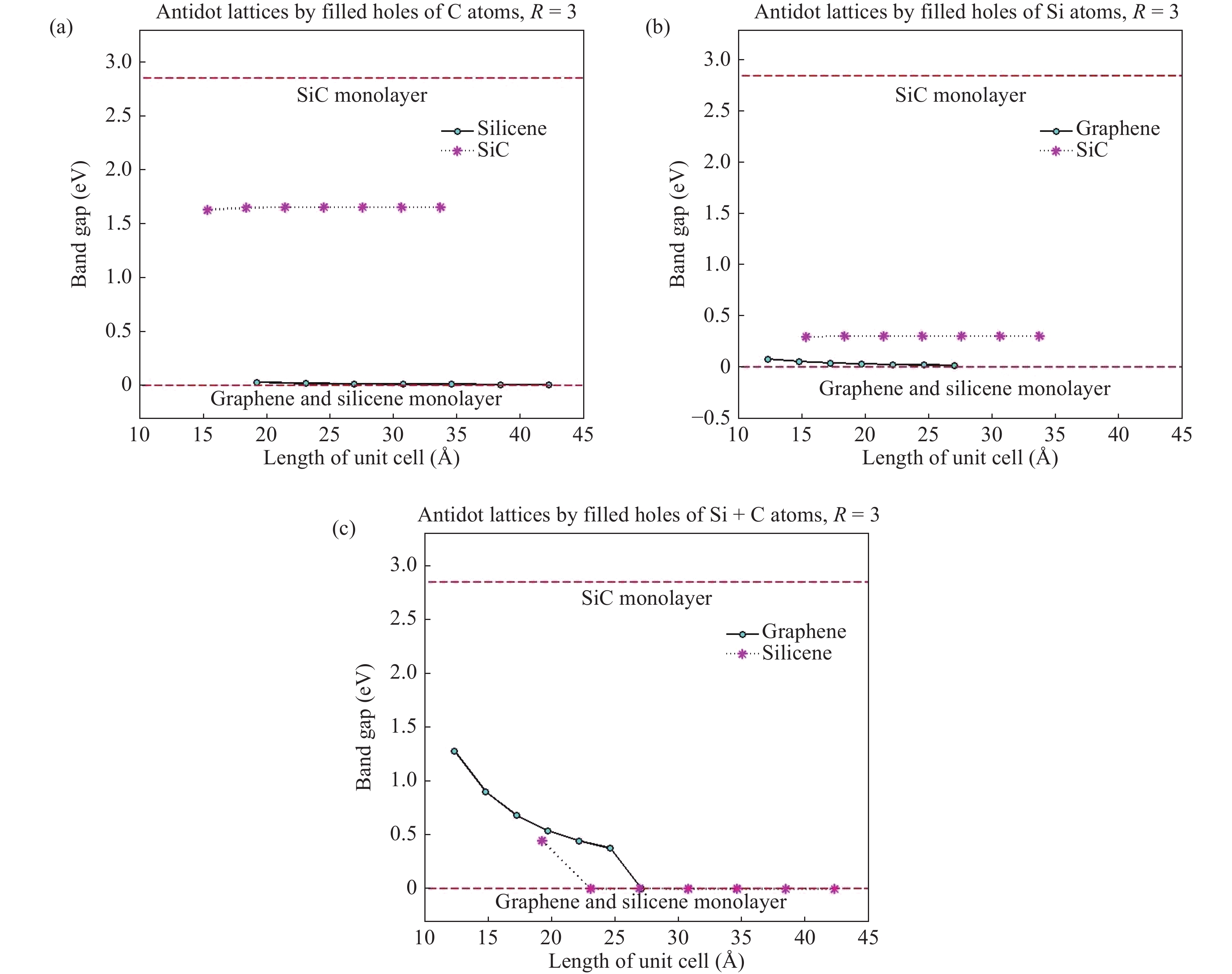
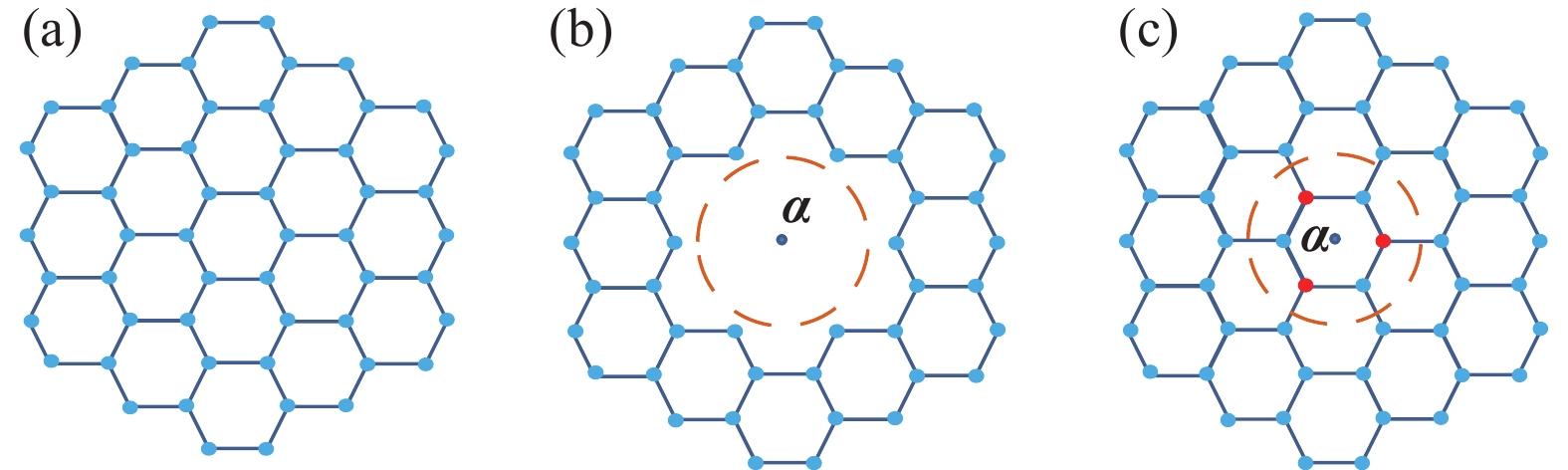
We have developed a$\pi$ -orbital tight-binding Hamiltonian model taking into account the nearest neighbors to study the effect of antidot lattices (two dimensional honeycomb lattice of atoms including holes) on the band structure of silicene and silicon carbide (SiC) sheets. We obtained that the band structure of the silicene antidot superlattice strongly depends on the size of embedded holes, and the band gap of the silicene antidot lattice increases by increasing of holes diameter. The band gap of SiC antidot lattice, except for the lattice of the small unit cell, is independent of the holes diameter and also depends on the distance between holes. We obtained that, the band gap of the SiC antidot lattice is the same as the band gap of the corresponding sheet without hole. Also, the electronic properties of the SiC antidot superlattice occupied either by carbon or by silicon atoms are investigated, numerically. Furthermore, we study the effect of occupation of graphene antidot by Si atoms and vice versa. Also, we have calculated the band structure of graphene and silicene antidot lattice filled by Si + C atoms. Finally, we compute the band structure of the SiC antidot lattice including the holes which are filled by C or by Si atoms. Really, in this paper we have generalized the method of paper[38 ] about graphene antidot with empty holes to the cases of filled holes by different atoms and also to the case of silicene and silicon carbide antidot lattices.-
Keywords:
- tight binding,
- band structure,
- antidot,
- graphene,
- silicene,
- SiC
-
References
[1] Bharech S, Kumar R. A review on the properties and applications of graphene. J Mater Sci Mechan Eng, 2015, 2(10): 70[2] Allen M J, Tung V C, Kaner R B. Honeycomb carbon: a review of graphene. Chem Rev, 2009, 110(1): 132[3] Choi W, Lee J W. Graphene: synthesis and applications. CRC Press, 2011[4] Chabot V, Higgins D, Yu A, et al. A review of graphene and graphene oxide sponge: material synthesis and applications to energy and the environment. Energy Environm Sci, 2014, 7(5): 1564 doi: 10.1039/c3ee43385d[5] Brunner K. Si/Ge nanostructures. Rep Prog Phys, 2001, 65(1): 27[6] Kara A, Enriquez H, Seitsonen A P, et al. A review on silicene—new candidate for electronics. Surf Sci Rep, 2012, 67(1): 1 doi: 10.1016/j.surfrep.2011.10.001[7] Chiew Y L, Cheong K Y. A review on the synthesis of SiC from plant-based biomasses. Mater Sci Eng B, 2011, 176(13): 951 doi: 10.1016/j.mseb.2011.05.037[8] Pecholt B, Gupta S, Molian P. Review of laser microscale processing of silicon carbide. J Laser Appl, 2011, 23(1): 012008 doi: 10.2351/1.3562522[9] Casady J, Johnson R. Status of silicon carbide (SiC) as a wide-band gap semiconductor for high-temperature applications: a review. Solid-State Electron, 1996, 39(10): 1409 doi: 10.1016/0038-1101(96)00045-7[10] Bekaroglu E, Topsakal M, Cahangirov S, et al. First-principles study of defects and adatoms in silicon carbide honeycomb structures. Phys Rev B, 2010, 81(7): 075433 doi: 10.1103/PhysRevB.81.075433[11] Ye X S, Shao Z G, Zhao H, et al. Electronic and optical properties of silicene nanomeshes. RSC Adv, 2014, 4(72): 37998 doi: 10.1039/C4RA03942D[12] Wright N G, Horsfall A B. SiC sensors: a review. J Phys D, 2007, 40(20): 6345 doi: 10.1088/0022-3727/40/20/S17[13] Shao Z G, Ye X S, Yang L, et al. First-principles calculation of intrinsic carrier mobility of silicene. J Appl Phys, 2013, 114(9): 093712 doi: 10.1063/1.4820526[14] Guzmán-Verri G G, Voon L L. Electronic structure of silicon-based nanostructures. Phys Rev B, 2007, 76(7): 075131 doi: 10.1103/PhysRevB.76.075131[15] Zheng F B, Zhang C W, Wang P J, et al. Novel half-metal and spin gapless semiconductor properties in N-doped silicene nanoribbons. J Appl Phys, 2013, 113(15): 154302 doi: 10.1063/1.4801882[16] Liu C C, Feng W, Yao Y. Quantum spin Hall effect in silicene and two-dimensional germanium. Phys Rev Lett, 2011, 107(7): 076802 doi: 10.1103/PhysRevLett.107.076802[17] Martinazzo R, Casolo S, Tantardini G F. Symmetry-induced band-gap opening in graphene superlattices. Phys Rev B, 2010, 81(24): 245420 doi: 10.1103/PhysRevB.81.245420[18] Trolle M L, Møller U S, Pedersen T G. Large and stable band gaps in spin-polarized graphene antidot lattices. Phys Rev B, 2013, 88(19): 195418 doi: 10.1103/PhysRevB.88.195418[19] Zhou W, Yan L, Wang Y, et al. SiC nanowires: a photocatalytic nanomaterial. Appl Phys Lett, 2006, 89(1): 013105 doi: 10.1063/1.2219139[20] Hu J Q, Bando Y, Zhan J H, et al. Fabrication of ZnS/SiC nanocables, SiC-shelled ZnS nanoribbons (and sheets), and SiC nanotubes (and tubes). Appl Phys Lett, 2004, 85(14): 2932 doi: 10.1063/1.1801168[21] De Padova P, Quaresima C, Ottaviani C, et al. Evidence of graphene-like electronic signature in silicene nanoribbons. Appl Phys Lett, 2010, 96(26): 261905 doi: 10.1063/1.3459143[22] Kim J, Kim Y H, Choi S H, et al. Curved silicon nanowires with ribbon-like cross sections by metal-assisted chemical etching. Acs Nano, 2011, 5(6): 5242 doi: 10.1021/nn2014358[23] Sun L, Li Y, Li Z, et al. Electronic structures of SiC nanoribbons. J Chem Phys, 2008, 129(17): 174114 doi: 10.1063/1.3006431[24] Baumeier B, Krüger P, Pollmann J. Structural, elastic, and electronic properties of SiC, BN, and BeO nanotubes. Phys Rev B, 2007, 76(8): 085407 doi: 10.1103/PhysRevB.76.085407[25] Menon M, Richter E, Mavrandonakis A, et al. Structure and stability of SiC nanotubes. Phys Rev B, 2004, 69(11): 115322 doi: 10.1103/PhysRevB.69.115322[26] Kara A, Vizzini S, Leandri C, et al. Silicon nano-ribbons on Ag (110): a computational investigation. J Phys: Condensed Matter, 2010, 22(4): 045004 doi: 10.1088/0953-8984/22/4/045004[27] Ding Y, Ni J. Electronic structures of silicon nanoribbons. Appl Phys Lett, 2009, 95(8): 083115 doi: 10.1063/1.3211968[28] Cahangirov S, Topsakal M, Aktürk E, et al. Two-and one-dimensional honeycomb structures of silicon and germanium. Phys Rev Lett, 2009, 102(23): 236804 doi: 10.1103/PhysRevLett.102.236804[29] Lehmann T, Ryndyk D A, Cuniberti G. Combined effect of strain and defects on the conductance of graphene nanoribbons. Phys Rev B, 2013, 88(12): 125420 doi: 10.1103/PhysRevB.88.125420[30] Sahin H, Ataca C, Ciraci S. Electronic and magnetic properties of graphane nanoribbons. Phys Rev B, 2010, 81(20): 205417 doi: 10.1103/PhysRevB.81.205417[31] Lu Y H, Feng Y P. Band-gap engineering with hybrid graphane–graphene nanoribbons. J Phys Chem C, 2009, 113(49): 20841 doi: 10.1021/jp9067284[32] Huang H, Wei D, Sun J, et al. Spatially resolved electronic structures of atomically precise armchair graphene nanoribbons. Sci Rep, 2012, 2: 983 doi: 10.1038/srep00983[33] Le Lay G, Aufray B, Léandri C, et al. Physics and chemistry of silicene nano-ribbons. Appl Surf Sci, 2009, 256(2): 524 doi: 10.1016/j.apsusc.2009.07.114[34] Balog R, Jørgensen B, Nilsson L, et al. Bandgap opening in graphene induced by patterned hydrogen adsorption. Nat Mater, 2010, 9(4): 315 doi: 10.1038/nmat2710[35] Zhang Y, Qin H, Cao E, et al. Ferromagnetism induced by intrinsic defects and boron substitution in single-wall SiC nanotubes. J Phys Chem A, 2011, 115(35): 9987 doi: 10.1021/jp109470r[36] Guzmán-Verri G G, Voon L L. Band structure of hydrogenated Si nanosheets and nanotubes. J Phys: Conden Matter, 2011, 23(14): 145502 doi: 10.1088/0953-8984/23/14/145502[37] Tachikawa H, Iyama T. Structures and electronic states of fluorinated graphene. Solid State Sci, 2014, 28: 41 doi: 10.1016/j.solidstatesciences.2013.12.014[38] Pedersen T G, Flindt C, Pedersen J, et al. Graphene antidot lattices: designed defects and spin qubits. Phys Rev Lett, 2008, 100(13): 136804 doi: 10.1103/PhysRevLett.100.136804[39] Ouyang F, Peng S, Yang Z, et al. Bandgap opening/closing of graphene antidot lattices with zigzag-edged hexagonal holes. Phys Chem Chem Phys, 2014, 16(38): 20524 doi: 10.1039/C4CP02090A[40] Oswald W, Wu Z. Energy gaps in graphene nanomeshes. Phys Rev B, 2012, 85(11): 115431 doi: 10.1103/PhysRevB.85.115431[41] Petersen R, Pedersen T G, Jauho A P. Clar sextets in square graphene antidot lattices. Physica E, 2012, 44(6): 967 doi: 10.1016/j.physe.2011.04.011[42] Zhang A, Teoh H F, Dai Z, et al. Band gap engineering in graphene and hexagonal BN antidot lattices: A first principles study. Appl Phys Lett, 2011, 98(2): 023105 doi: 10.1063/1.3536517[43] Petersen R, Pedersen T G, Jauho A P. Clar sextet analysis of triangular, rectangular, and honeycomb graphene antidot lattices. Acs Nano, 2010, 5(1): 523[44] Sahin H, Ciraci S. Structural, mechanical, and electronic properties of defect-patterned graphene nanomeshes from first principles. Phys Rev B, 2011, 84(3): 035452 doi: 10.1103/PhysRevB.84.035452[45] Ouyang F, Peng S, Liu Z, et al. Bandgap opening in graphene antidot lattices: the missing half. ACS Nano, 2011, 5(5): 4023 doi: 10.1021/nn200580w[46] Ouyang F, Yang Z, Xiao J, et al. Electronic structure and chemical modification of graphene antidot lattices. J Phys Chem C, 2010, 114(37): 15578 doi: 10.1021/jp1028454[47] Petersen R, Pedersen T G. Quasiparticle properties of graphene antidot lattices. Phys Rev B, 2009, 80(11): 113404 doi: 10.1103/PhysRevB.80.113404[48] Liu W, Wang Z F, Shi Q W, et al. Band-gap scaling of graphene nanohole superlattices. Phys Rev B, 2009, 80(23): 233405 doi: 10.1103/PhysRevB.80.233405[49] Fürst J A, Pedersen T G, Brandbyge M, et al. Density functional study of graphene antidot lattices: Roles of geometrical relaxation and spin. Phys Rev B, 2009, 80(11): 115117 doi: 10.1103/PhysRevB.80.115117[50] Yu D, Lupton E M, Liu M, et al. Collective magnetic behavior of graphene nanohole superlattices. Nano Res, 2008, 1(1): 56 doi: 10.1007/s12274-008-8007-6[51] Bai J, Zhong X, Jiang S, et al. Graphene nanomesh. Nat Nanotechnol, 2010, 5(3): 190 doi: 10.1038/nnano.2010.8[52] Kim M, Safron N S, Han E, at al. Fabrication and characterization of large-area, semiconducting nanoperforated graphene materials. Nano Lett, 2010, 10(4): 1125 doi: 10.1021/nl9032318[53] Liang X, Jung Y S, Wu S, et al. Formation of bandgap and subbands in graphene nanomeshes with sub-10 nm ribbon width fabricated via nanoimprint lithography. Nano Lett, 2010, 10(7): 2454 doi: 10.1021/nl100750v[54] Heydrich S, Hirmer M, Preis C, et al. Scanning Raman spectroscopy of graphene antidot lattices: evidence for systematic p-type doping. Appl Phys Lett, 2010, 97(4): 043113 doi: 10.1063/1.3474613[55] Shen T, Wu Y Q, Capano M A, et al. Magnetoconductance oscillations in graphene antidot arrays. Appl Phys Lett, 2008, 93(12): 122102 doi: 10.1063/1.2988725[56] Sinitskii A, Tour J M. Patterning graphene through the self-assembled templates: toward periodic two-dimensional graphene nanostructures with semiconductor properties. J Am Chem Soc, 2010, 132(42): 14730 doi: 10.1021/ja105426h[57] Freeman C L, Claeyssens F, Allan N L, et al. Graphitic nanofilms as precursors to wurtzite films: theory. Phys Rev Lett, 2006, 96(6): 066102 doi: 10.1103/PhysRevLett.96.066102[58] Chiappe D, Grazianetti C, Tallarida G, et al. Local electronic properties of corrugated silicene phases. Adv Mater, 2012, 25; 24(37): 5088[59] Sahin H, Cahangirov S, Topsakal M, et al. Monolayer honeycomb structures of group-IV elements and III–V binary compounds: first-principles calculations. Phys Rev B, 2009, 80(15): 155453 doi: 10.1103/PhysRevB.80.155453[60] Pan F, Wang Y, Jiang K, et al. Silicene nanomesh. Sci Rep, 2015, 5[61] Zhao K, Zhao M, Wang Z, et al. Tight-binding model for the electronic structures of SiC and BN nanoribbons. Physica E, 2010, 43(1): 440 doi: 10.1016/j.physe.2010.08.025[62] Saito R, Dresselhaus G, Dresselhaus M S. Physical properties of carbon nanotubes. World Scientific, 1998[63] Slater J C, Koster G F. Simplified LCAO method for the periodic potential problem. Phys Rev, 1954, 94(6): 1498 doi: 10.1103/PhysRev.94.1498[64] Jung J, MacDonald A H. Carrier density and magnetism in graphene zigzag nanoribbons. Phys Rev B, 2009, 79(23): 235433 doi: 10.1103/PhysRevB.79.235433[65] Hannewald K, Stojanović V M, Schellekens J M, et al. Theory of polaron bandwidth narrowing in organic molecular crystals. Phys Rev B, 2004, 69(7): 075211 doi: 10.1103/PhysRevB.69.075211[66] Novoselov K S, Geim A K, Morozov S, et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature, 2005, 438(7065): 197 doi: 10.1038/nature04233[67] Berger C, Song Z, Li X, et al. Electronic confinement and coherence in patterned epitaxial graphene. Science, 2006, 312(5777): 1191 doi: 10.1126/science.1125925[68] Han M Y, Özyilmaz B, Zhang Y, et al. Energy band-gap engineering of graphene nanoribbons. Phys Rev Lett, 2007, 98(20): 206805 doi: 10.1103/PhysRevLett.98.206805[69] Geim A K, Novoselov K S. The rise of graphene. Nat Mater, 2007, 6(3): 183 doi: 10.1038/nmat1849 -
Proportional views






 DownLoad:
DownLoad: