| Citation: |
Pedram Jahandar, Maksym Myronov. Impact of strain relaxation on the growth rate of heteroepitaxial germanium tin binary alloy[J]. Journal of Semiconductors, 2024, 45(10): 102101. doi: 10.1088/1674-4926/24030002
****
P Jahandar and M Myronov, Impact of strain relaxation on the growth rate of heteroepitaxial germanium tin binary alloy[J]. J. Semicond., 2024, 45(10), 102101 doi: 10.1088/1674-4926/24030002
|
Impact of strain relaxation on the growth rate of heteroepitaxial germanium tin binary alloy
DOI: 10.1088/1674-4926/24030002
CSTR: 32376.14.1674-4926.24030002
More Information-
Abstract
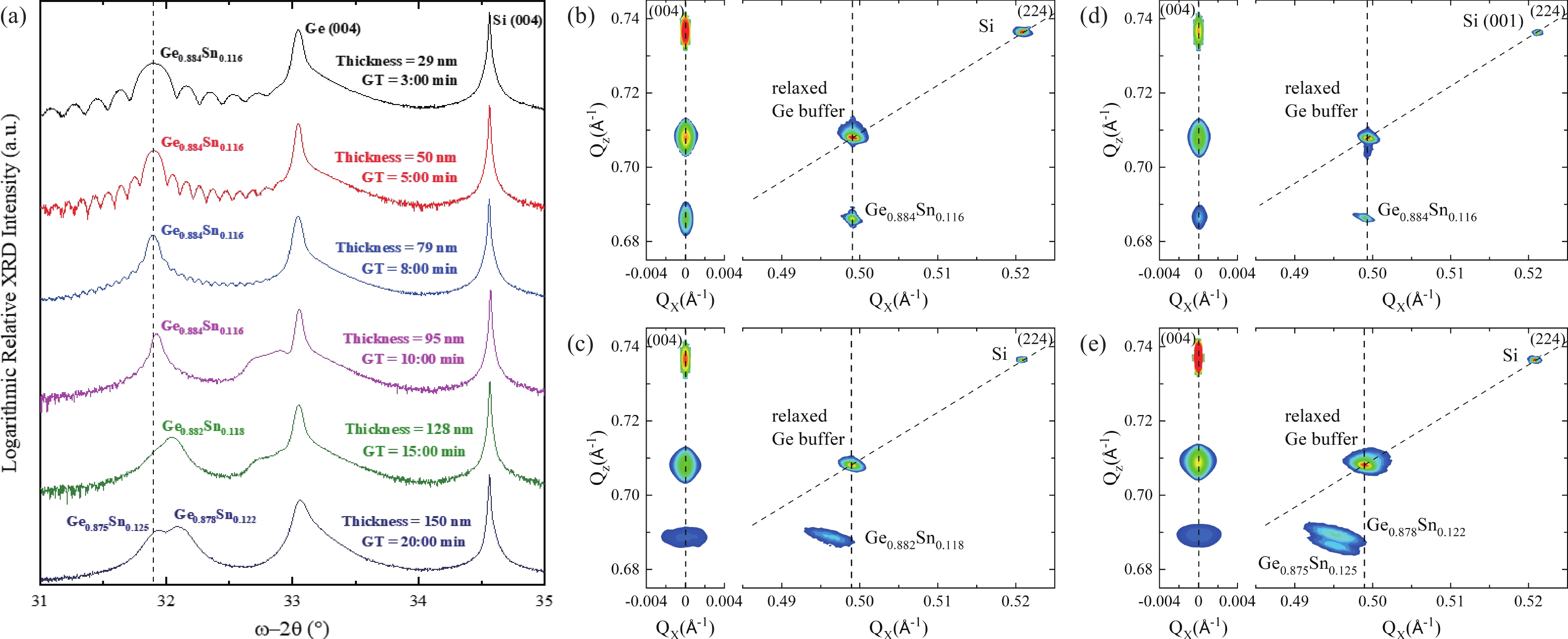
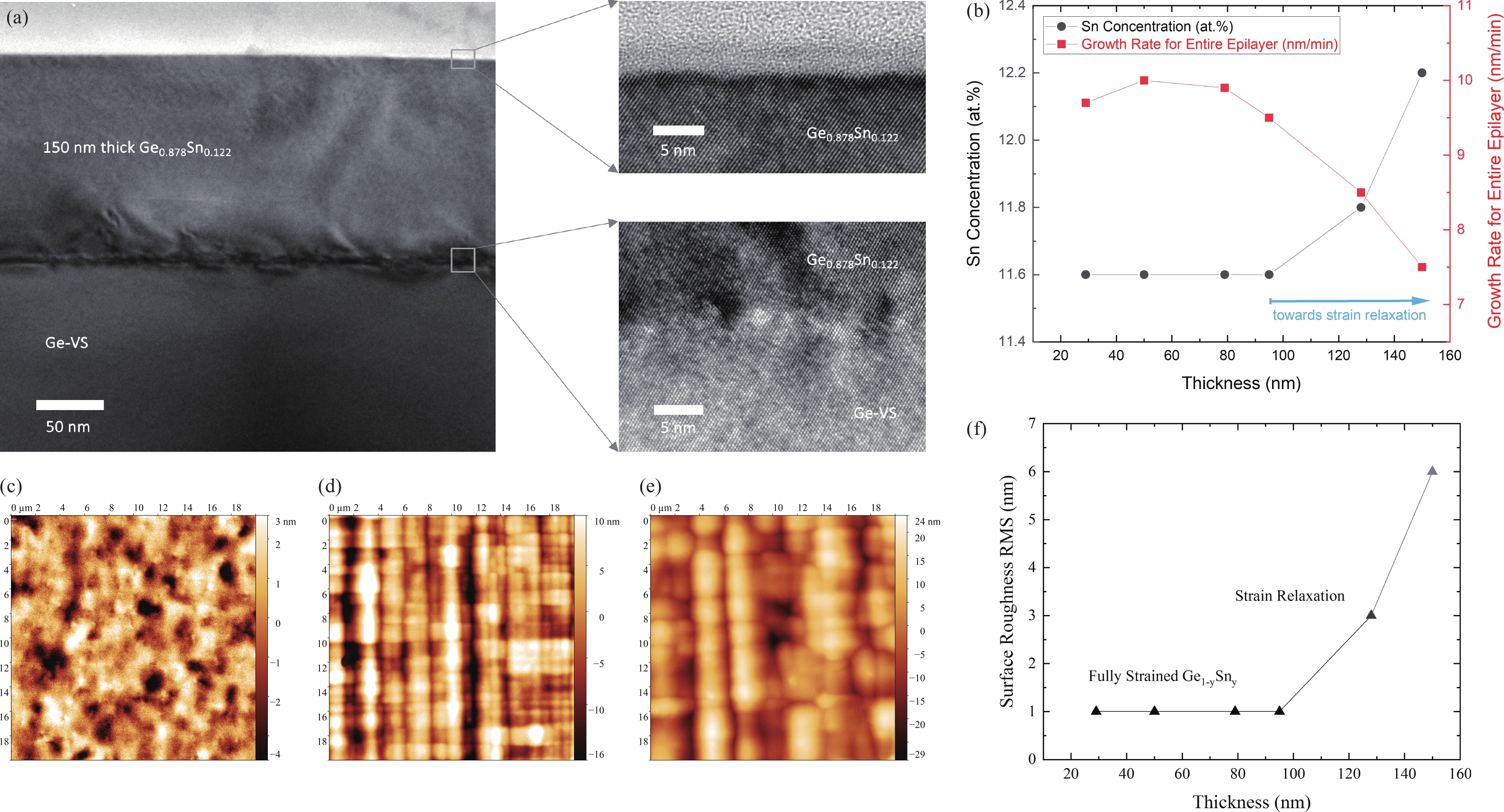
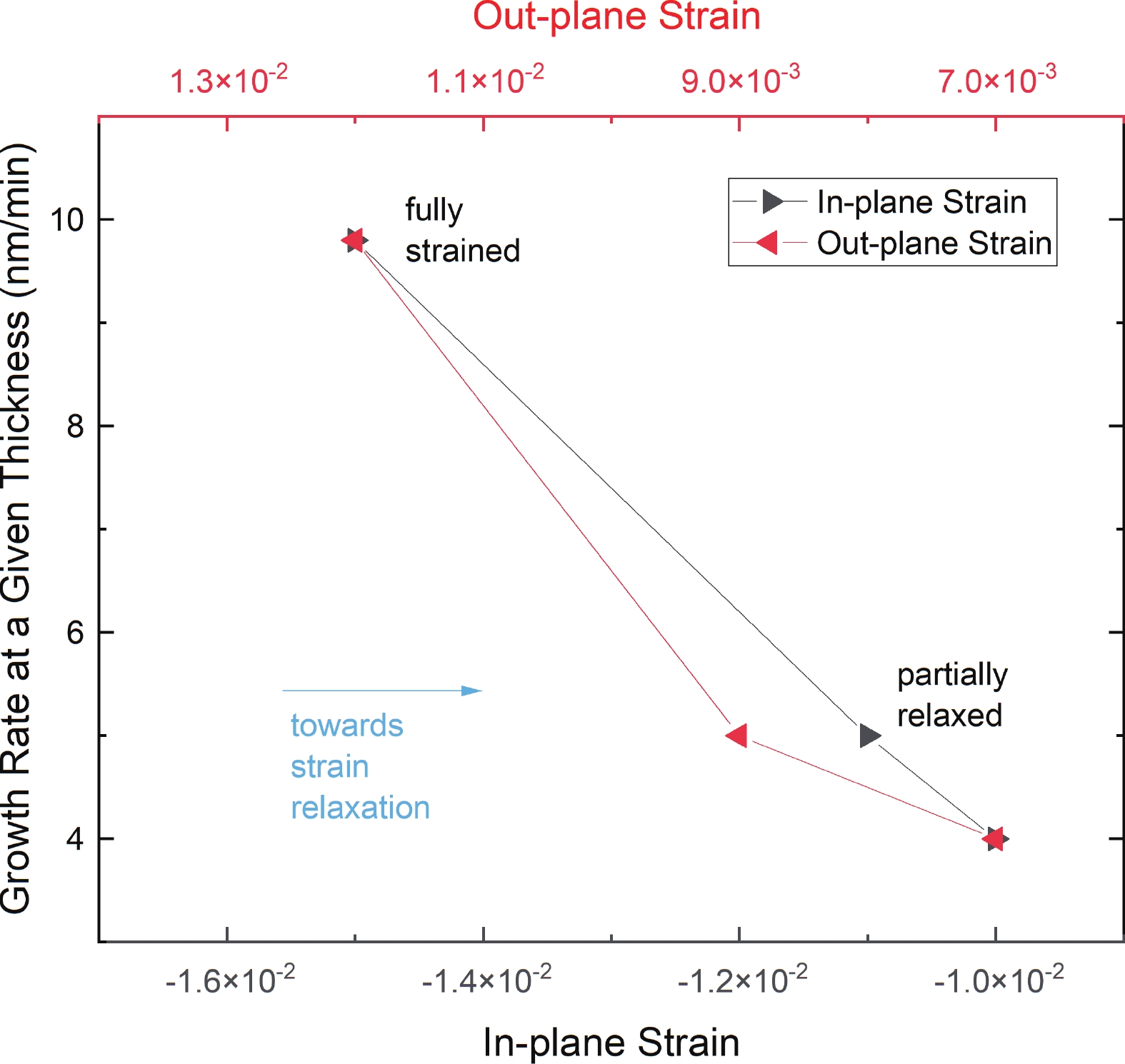
The growth of high-quality germanium tin (Ge1–ySny) binary alloys on a Si substrate using chemical vapor deposition (CVD) techniques holds immense potential for advancing electronics and optoelectronics applications, including the development of efficient and low-cost mid-infrared detectors and light sources. However, achieving precise control over the Sn concentration and strain relaxation of the Ge1–ySny epilayer, which directly influence its optical and electrical properties, remain a significant challenge. In this research, the effect of strain relaxation on the growth rate of Ge1–ySny epilayers, with Sn concentration >11at.%, is investigated. It is successfully demonstrated that the growth rate slows down by ~55% due to strain relaxation after passing its critical thickness, which suggests a reduction in the incorporation of Ge into Ge1–ySny growing layers. Despite the increase in Sn concentration as a result of the decrease in the growth rate, it has been found that the Sn incorporation rate into Ge1–ySny growing layers has also decreased due to strain relaxation. Such valuable insights could offer a foundation for the development of innovative growth techniques aimed at achieving high-quality Ge1–ySny epilayers with tuned Sn concentration and strain relaxation. -
References
[1] Johnson E R, Christian S M. Some properties of germanium-silicon alloys. Phys Rev, 1954, 95, 560 doi: 10.1103/PhysRev.95.560[2] Göbel E O, Ploog K. Fabrication and optical properties of semiconductor quantum wells and superlattices. Prog Quantum Electron, 1990, 14, 289 doi: 10.1016/0079-6727(90)90001-E[3] Joyce B A. Materials fundamentals of molecular beam epitaxy. Adv Mater, 1993, 5, 773 doi: 10.1002/adma.19930051028[4] Gupta S, Magyari-Köpe B, Nishi Y, et al. Achieving direct band gap in germanium through integration of Sn alloying and external strain. J Appl Phys, 2013, 113, 73707 doi: 10.1063/1.4792649[5] Wirths S, Buca D, Mantl S. Si–Ge–Sn alloys: From growth to applications. Prog Cryst Growth Charact Mater, 2016, 62, 1 doi: 10.1016/j.pcrysgrow.2015.11.001[6] Lieten R R, Maeda T, Jevasuwan W, et al. Tensile-strained GeSn metal–oxide–semiconductor field-effect transistor devices on Si(111) using solid phase epitaxy. Appl Phys Express, 2013, 6, 101301 doi: 10.7567/APEX.6.101301[7] Guo P F, Han G Q, Gong X, et al. Ge0.97Sn0.03 p-channel metal-oxide-semiconductor field-effect transistors: Impact of Si surface passivation layer thickness and post metal annealing. J Appl Phys, 2013, 114, 044510 doi: 10.1063/1.4816695[8] Eckhardt C, Hummer K, Kresse G. Indirect-to-direct gap transition in strained and unstrained Sn xGe1– x alloys. Phys Rev B, 2014, 89, 165201 doi: 10.1103/PhysRevB.89.165201[9] Zheng J, Liu Z, Xue C L, et al. Recent progress in GeSn growth and GeSn-based photonic devices. J Semicond, 2018, 39, 061006 doi: 10.1088/1674-4926/39/6/061006[10] Oguz S, Paul W, Deutsch T F, et al. Synthesis of metastable, semiconducting Ge-Sn alloys by pulsed UV laser crystallization. Appl Phys Lett, 1983, 43, 848 doi: 10.1063/1.94524[11] Soref R A, Friedman L. Direct-gap Ge/GeSn/Si and GeSn/Ge/Si heterostructures. Superlattices Microstruct, 1993, 14, 189 doi: 10.1006/spmi.1993.1122[12] Gurdal O, Desjardins P, Carlsson J R A, et al. Low-temperature growth and critical epitaxial thicknesses of fully strained metastable Ge1– xSnx (x≤0.26) alloys on Ge(001)2 × 1. J Appl Phys, 1998, 83, 162 doi: 10.1063/1.366690[13] Mosleh A, Ghetmiri S A, Conley B R, et al. Material characterization of Ge1− xSn xAlloys grown by a commercial CVD system for optoelectronic device applications. J Electron Mater, 2014, 43, 938 doi: 10.1007/s11664-014-3089-2[14] Wang W, Zhou Q, Dong Y, et al. Critical thickness for strain relaxation of Ge1–i>xSnx (x ≤ 0.17) grown by molecular beam epitaxy on Ge(001). Appl Phys Lett, 2015, 106, 232106 doi: 10.1063/1.4922529[15] Gencarelli F, Vincent B, Demeulemeester J, et al. Crystalline properties and strain relaxation mechanism of CVD grown GeSn. ECS J Solid State Sci Technol, 2013, 2, P134 doi: 10.1149/2.011304jss[16] Bhargava N, Coppinger M, Prakash Gupta J, et al. Lattice constant and substitutional composition of GeSn alloys grown by molecular beam epitaxy. Appl Phys Lett, 2013, 103, 041908 doi: 10.1063/1.4816660[17] Takeuchi S, Sakai A, Yamamoto K, et al. Growth and structure evaluation of strain-relaxed Ge1– xSn x buffer layers grown on various types of substrates. Semicond Sci Technol, 2007, 22, S231 doi: 10.1088/0268-1242/22/1/S54[18] Takeuchi S, Shimura Y, Nakatsuka O, et al. Growth of highly strain-relaxed Ge1– xSnx/virtual Ge by a Sn precipitation controlled compositionally step-graded method. Appl Phys Lett, 2008, 92, 231916 doi: 10.1063/1.2945629[19] Takeuchi S, Sakai A, Nakatsuka O, et al. Tensile strained Ge layers on strain-relaxed Ge1–xSnx/virtual Ge substrates. Thin Solid Films, 2008, 517, 159 doi: 10.1016/j.tsf.2008.08.068[20] Wirths S, Tiedemann A T, Ikonic Z, et al. Band engineering and growth of tensile strained Ge/(Si)GeSn heterostructures for tunnel field effect transistors. Appl Phys Lett, 2013, 102, 192103 doi: 10.1063/1.4805034[21] Weisshaupt D, Jahandar P, Colston G, et al. Impact of Sn segregation on Ge1− xSnx epi-layers growth by RP-CVD. 2017 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), 2017, 43 doi: 10.23919/MIPRO.2017.7973388[22] Jahandar P, Weisshaupt D, Colston G, et al. The effect of Ge precursor on the heteroepitaxy of Ge1– xSn x epilayers on a Si (001) substrate. Semicond Sci Technol, 2018, 33, 034003 doi: 10.1088/1361-6641/aa9e7e[23] Lu Low K, Yang Y, Han G Q, et al. Electronic band structure and effective mass parameters of Ge1- xSnx alloys. J Appl Phys, 2012, 112, 103106 doi: 10.1063/1.4765736[24] Tonkikh A A, Eisenschmidt C, Talalaev V G, et al. Pseudomorphic GeSn/Ge(001) quantum wells: Examining indirect band gap bowing. Appl Phys Lett, 2013, 103, 032106 doi: 10.1063/1.4813913[25] Dutt B, Lin H, Sukhdeo D S, et al. Theoretical analysis of GeSn alloys as a gain medium for a Si-compatible laser. IEEE J Sel Top Quantum Electron, 2013, 19, 1502706 doi: 10.1109/JSTQE.2013.2241397[26] Ionescu A M, Riel H. Tunnel field-effect transistors as energy-efficient electronic switches. Nature, 2011, 479, 329 doi: 10.1038/nature10679[27] Kotlyar R, Avci U E, Cea S, et al. Bandgap engineering of group IV materials for complementary n and p tunneling field effect transistors. Appl Phys Lett, 2013, 102, 113106 doi: 10.1063/1.4798283[28] Olesinski R W, Abbaschian G J. The Ge−Sn (Germanium−Tin) system. Bull Alloy Phase Diagr, 1984, 5, 265 doi: 10.1007/BF02868550[29] Fleurial J P, Borshchevsky A. Si-Ge-metal ternary phase diagram calculations. J Electrochem Soc, 1990, 137, 2928 doi: 10.1149/1.2087101[30] Zaima S, Nakatsuka O, Taoka N, et al. Growth and applications of GeSn-related Group-IV semiconductor materials. Sci Technol Adv Mater, 2015, 16, 043502 doi: 10.1088/1468-6996/16/4/043502 -
Proportional views





 Pedram Jahandar earned his PhD from the University of Warwick after obtaining his Bachelor of Science and Master of Science degrees from King’s College London. He specialises in Group Ⅳ semiconductor CVD epitaxy and device fabrication, and actively applies the latest technological advancements and academic achievements across various industries.
Pedram Jahandar earned his PhD from the University of Warwick after obtaining his Bachelor of Science and Master of Science degrees from King’s College London. He specialises in Group Ⅳ semiconductor CVD epitaxy and device fabrication, and actively applies the latest technological advancements and academic achievements across various industries.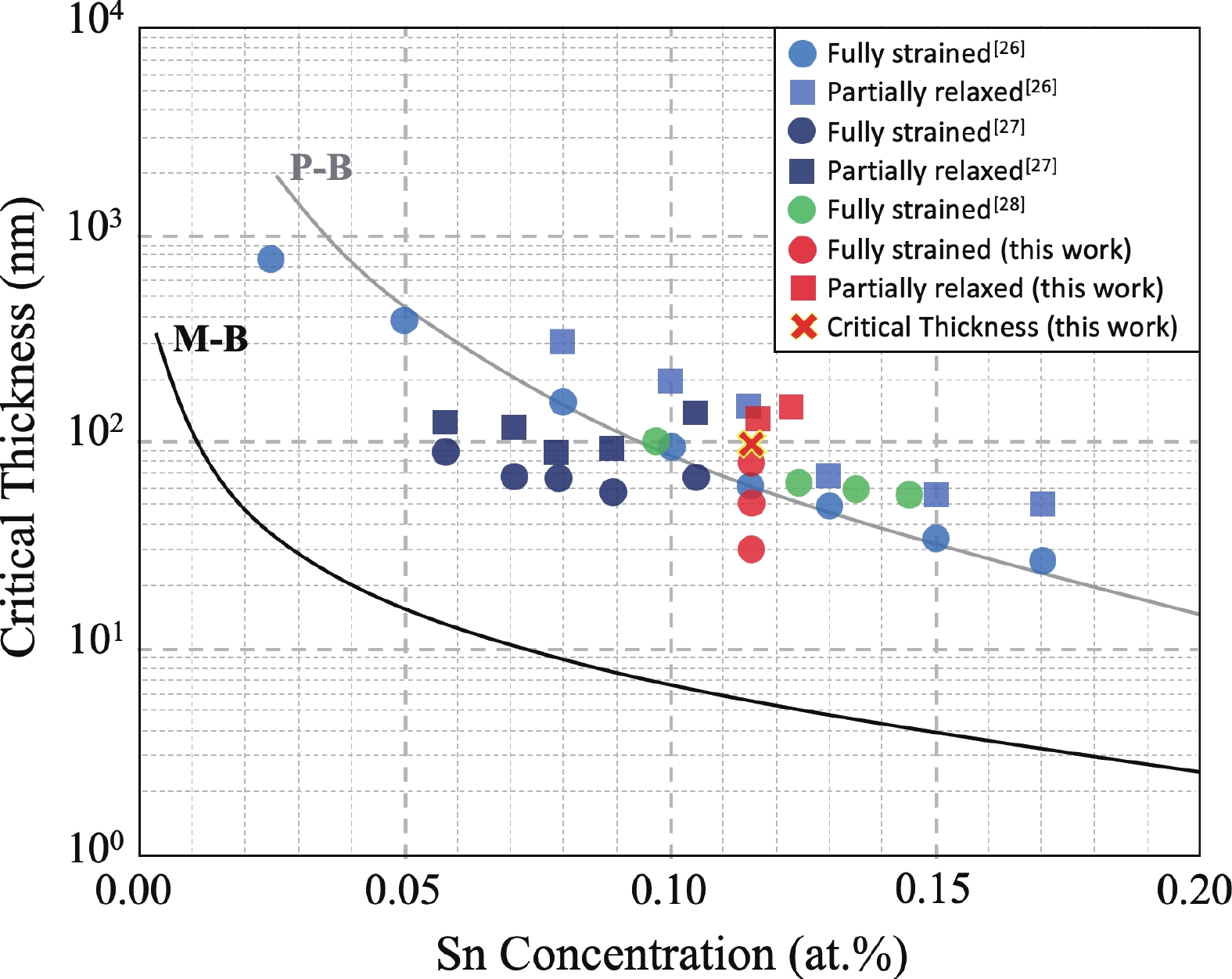
 DownLoad:
DownLoad: