| Citation: |
K Sivasankaran, P S Mallick. Stability performance of optimized symmetric DG-MOSFET[J]. Journal of Semiconductors, 2013, 34(10): 104001. doi: 10.1088/1674-4926/34/10/104001
****
K Sivasankaran, P S Mallick. Stability performance of optimized symmetric DG-MOSFET[J]. J. Semicond., 2013, 34(10): 104001. doi: 10.1088/1674-4926/34/10/104001.
|
Stability performance of optimized symmetric DG-MOSFET
DOI: 10.1088/1674-4926/34/10/104001
More Information
-
Abstract
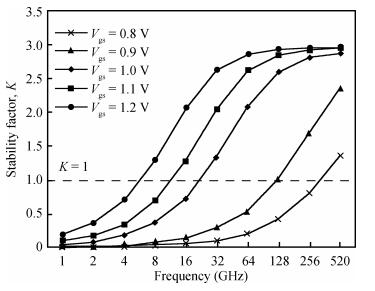
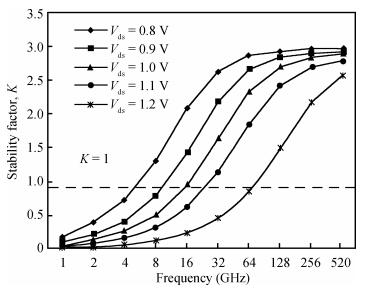
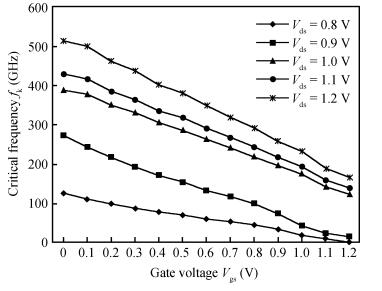
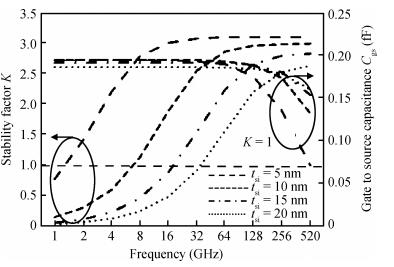
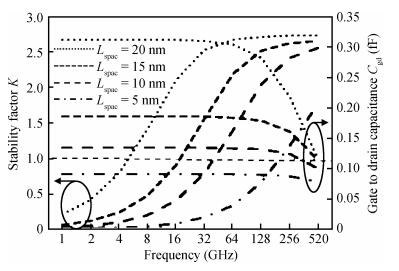
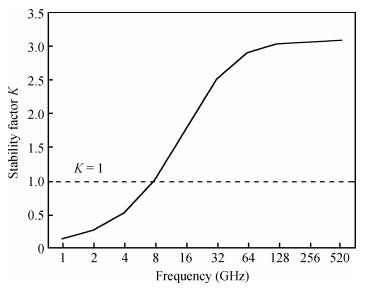
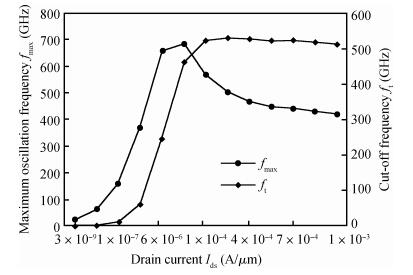
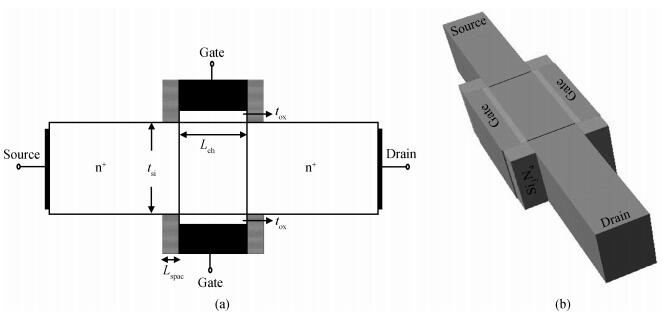
This article presents the bias and geometry optimization procedure for the radio frequency (RF) stability performance of nanoscale symmetric double-gate metal-oxide semiconductor field-effect transistors (DG-MOSFETs). The stability model can provide hints for optimizing the DG-MOSFET under an RF range. The device parameters are extracted for different bias and geometry conditions through numerical simulation, and the RF figures of merit such as cut-off frequency (ft) and maximum oscillation frequency (fmax), along with stability factor, are calculated for an optimized structure. The proposed structure exhibits good RF stability performance.-
Keywords:
- DG-MOSFET,
- radio frequency,
- stability factor,
- numerical simulation
-
References
[1] Wong H S P. Beyond the conventional transistor. IBM Journal of Research and Development, 2002, 6(2.3):133 https://www.coursehero.com/file/16360364/Beyond-the-Transistor/[2] Sorin C, Gacuteéard G, Thierry O, et al. Ultimately thin double-gate SOI MOSFETs. IEEE Trans Electron Devices, 2003, 50(3):830 doi: 10.1109/TED.2003.811371[3] Liang J, Xiao H, Huang R, et al. Design optimization of structural parameters in double gate MOSFETs for RF application. Semicond Sci Technol, 2008, 23(5):1 doi: 10.1007%2F978-3-642-19542-6_93.pdf[4] Mohankumar N, Syamal B, Sarkar C K. Influence of channel and gate engineering on the analog and RF performance of DG MOSFETs. IEEE Trans Electron Devices, 2010, 57(4):820 doi: 10.1109/TED.2010.2040662[5] Sharma R K, Gupta M, Gupta R S. TCAD assessment of device design technologies for enhanced performance of nanoscale DG MOSFET. IEEE Trans Electron Devices, 2011, 58(9):2936 doi: 10.1109/TED.2011.2160065[6] Sivasankaran K, Kannadassan D, Seetaram K, et al. Bias and geometry optimization of silicon nanowire transistor:radio frequency stability perspective. Microw Opt Technol Lett, 2012, 54(9):2114 doi: 10.1002/mop.27016[7] International Technology Roadmaps for Semiconductor (ITRS), 2005[8] Device simulator ATLAS user manual. Silvaco Int. , Santa Clara, CA, May 2006[Online Available]: http://silvaco.com[9] Schwierz F, Liou J J. Semiconductor devices for RF applications:evolution and current status. Microelectron Reliab, 2001, 41:145 doi: 10.1016/S0026-2714(00)00076-7[10] Gonzales G. Microwave transistor amplifiers——analysis and design. 2nd ed. Prentice-Hall, 1997[11] Rollet J M. Stability and power gain invariants of linear two ports. IRE Trans Circuit Theory, 1962, 9:29 doi: 10.1109/TCT.1962.1086854[12] Cho S, Kim K R, Park B G, et al. RF performance and small-signal parameter extraction of junctionless silicon nanowire MOSFETs. IEEE Trans Electron Devices, 2011, 58(5):1388 doi: 10.1109/TED.2011.2109724[13] Sarkar A, Das A K, De S, et al. Effect of gate engineering in double-gate MOSFETs for analog/RF applications. Microelectron J, 2012, 43(11):873 doi: 10.1016/j.mejo.2012.06.002 -
Proportional views





 DownLoad:
DownLoad: