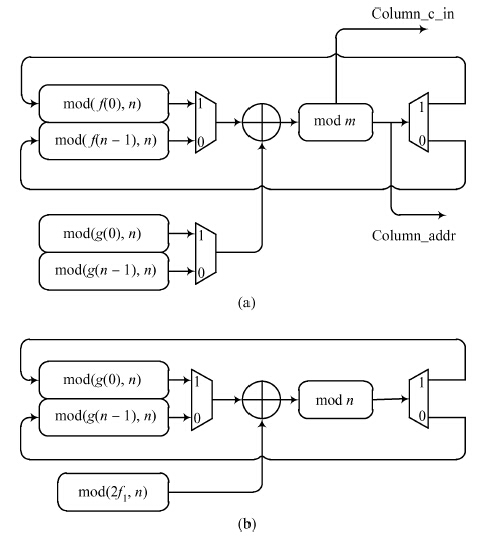
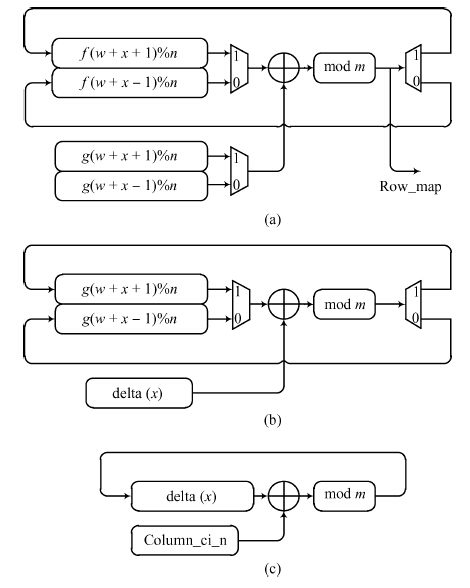
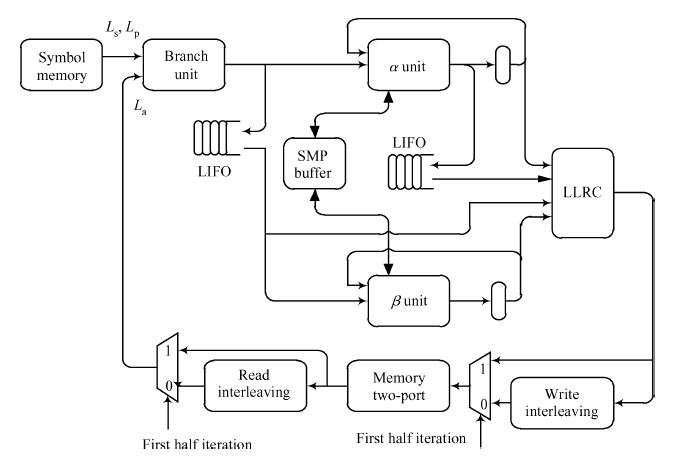
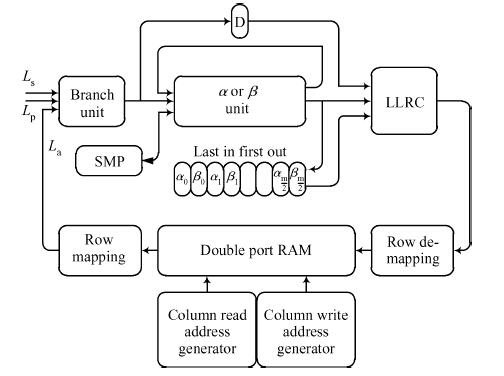
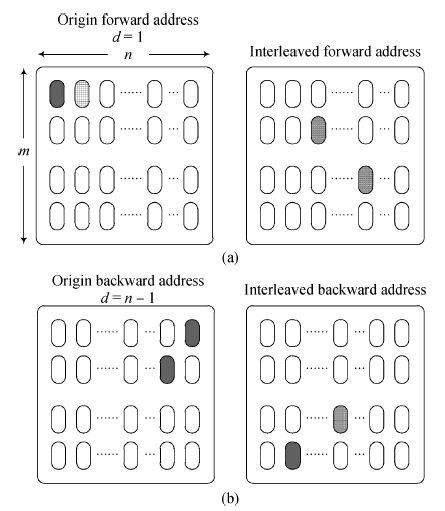
Abstract: This paper presents a turbo decoder supporting all 188 block sizes in 3GPP long term evolution (LTE) standard which can be employed in the LTE micro-eNodB system. The design allows 1, 2, 4, 8 or 16 soft-in/soft-out (SISO) decoders to concurrently process each block size, and the number of iterations can be adjusted. This article proposes an improved SISO algorithm and interleaving design, calculated forward state matrix and backward state matrix alternately, and the branch transition probability can be used in the Turbo decode process directly just after one clock delay. The structure enables a decoder processing radix-2 algorithm with high speed, instead of radix-4 as the conventional decoder. Moreover, the paper details an interleaver/de-interleaver, which is combined by two operational steps. One is column address mapping and the other is intra-row permutation. Decoder realizes interleaving by loading data from memories whose address is generated by column mapping and then lets data passing through inter-row permutation. For de-interleaving, the system can adopt reverse operation.

Key words: LTE, turbo decoder, (quadratic polynomial permutation) QPP interleaver