J. Semicond. > 2016, Volume 37 > Issue 2 > 025001
|

SEMICONDUCTOR INTEGRATED CIRCUITS

High-stage analog accumulator for TDI CMOS image sensors

Jianxin Li, Fujun Huang, Yong Zong and Jing Gao

+ Author Affiliations

 Corresponding author: Jing Gao, Email: gaojing@tju.edu.cn

DOI: 10.1088/1674-4926/37/2/025001

PDF

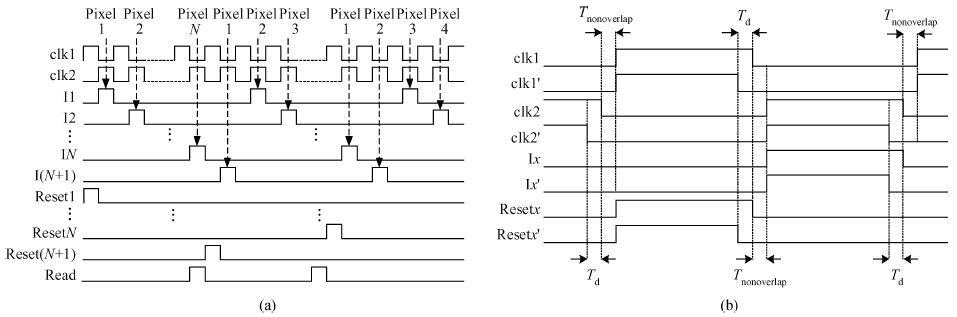
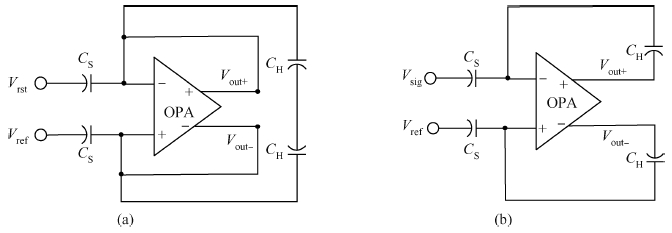
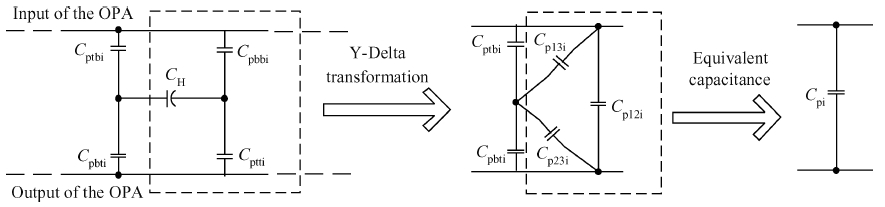
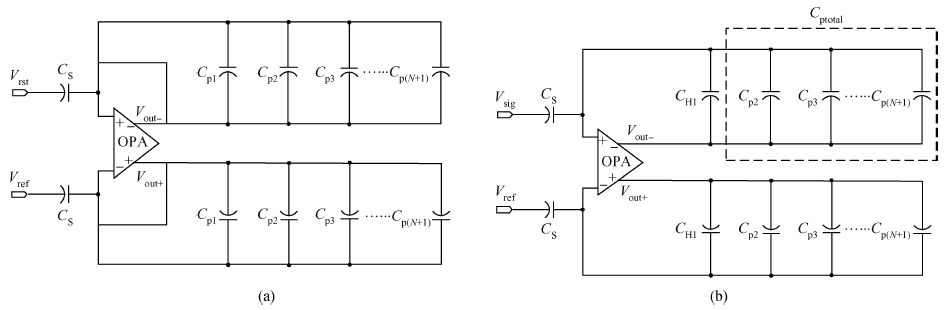
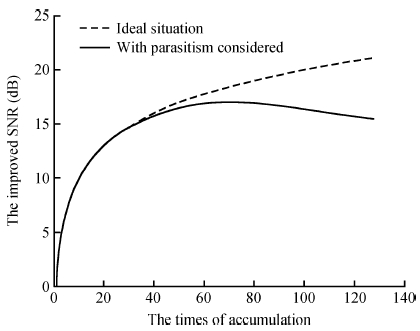
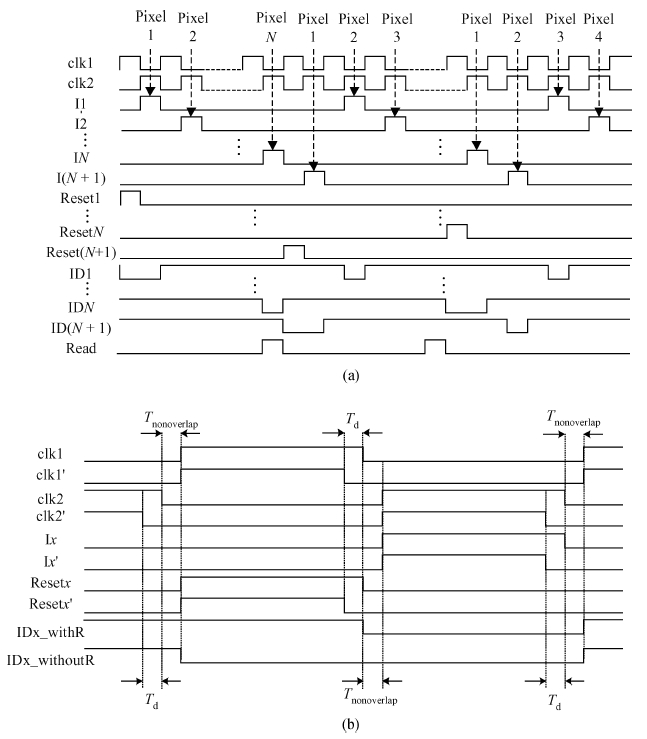
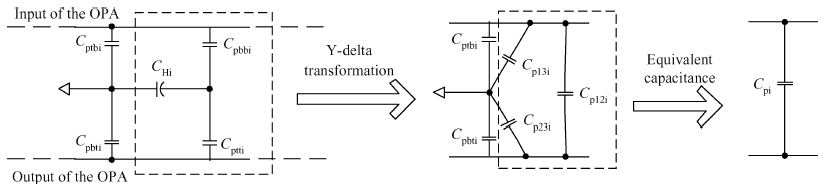
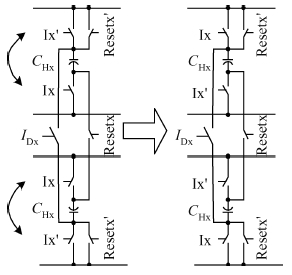
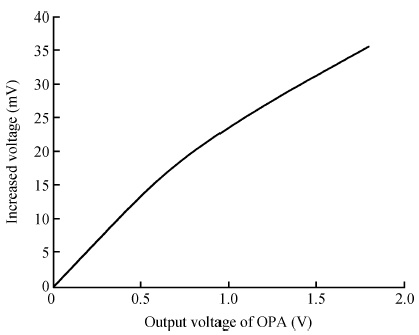
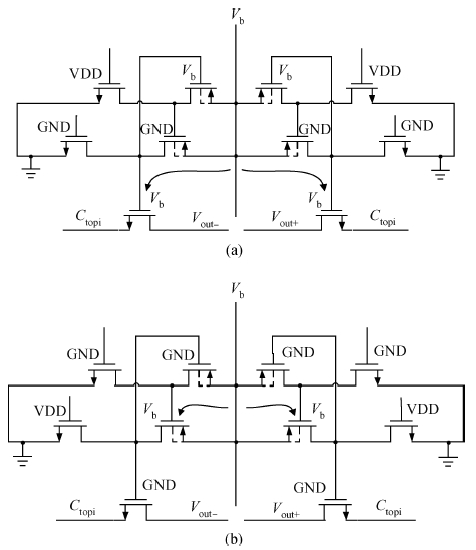
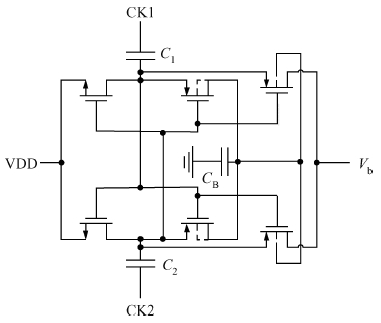
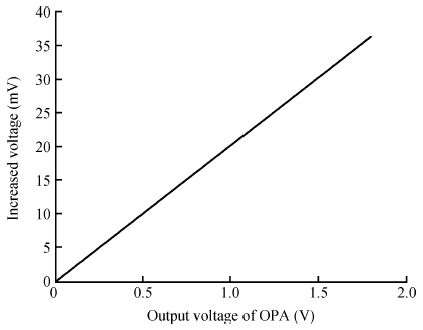
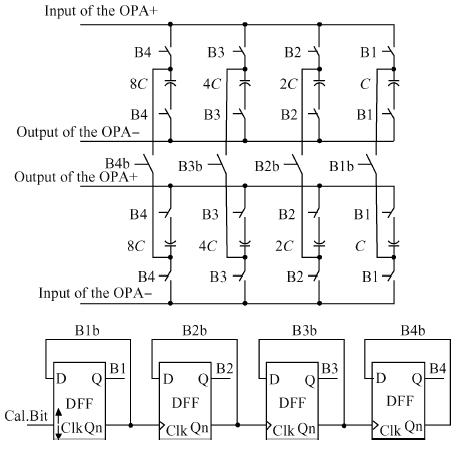
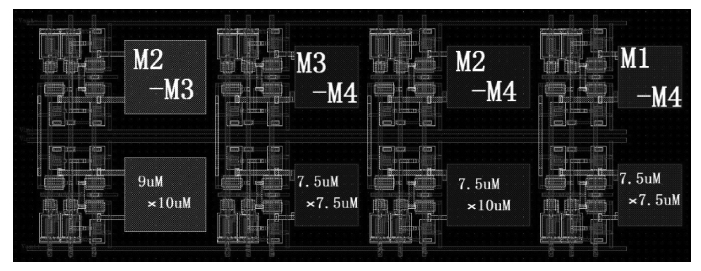
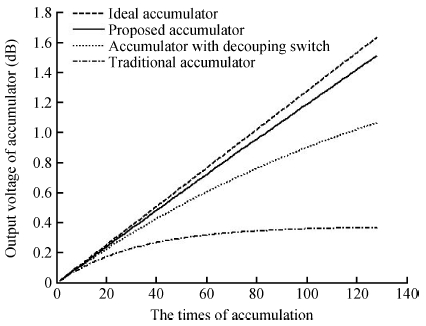
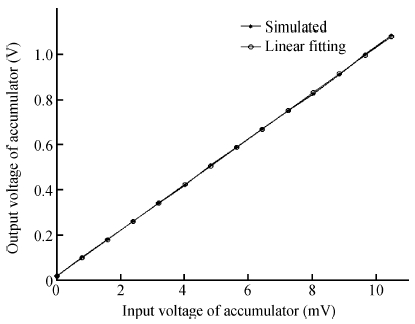
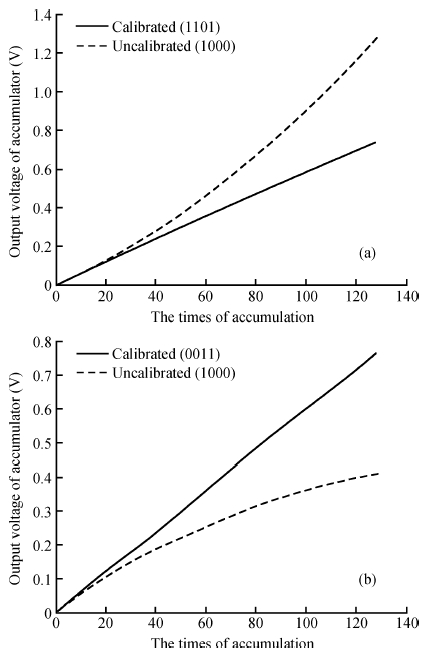
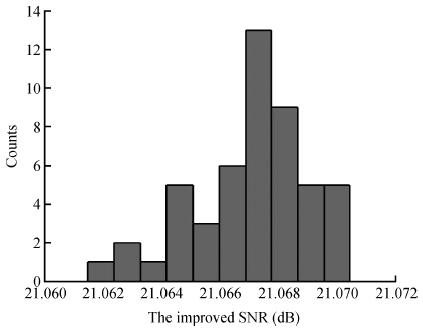
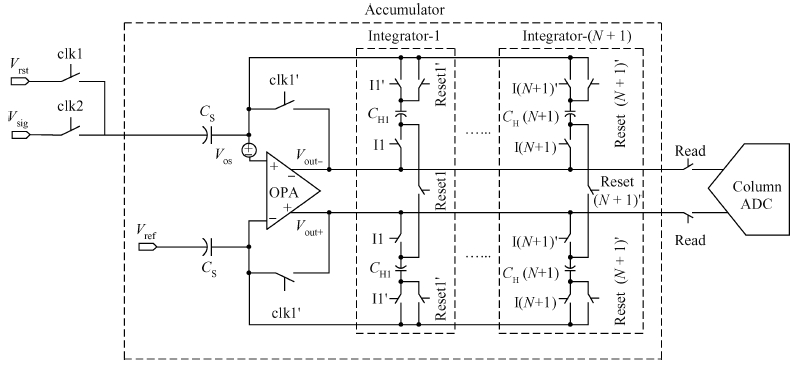
Abstract: The impact of the parasitic phenomenon on the performance of the analog accumulator in TDI CMOS image sensor is analyzed and resolved. A 128-stage optimized accumulator based on 0.18-μ m one-poly four-metal 3.3 V CMOS technology is designed and simulated. A charge injection effect from the top plate sampling is employed to compensate the un-eliminated parasitics based on the accumulator with a decoupling switch, and then a calibration circuit is designed to restrain the mismatch and Process, Voltage and Temperature (PVT) variations. The post layout simulation indicates that the improved SNR of the accumulator upgrades from 17.835 to 21.067 dB, while an ideal value is 21.072 dB. In addition, the linearity of the accumulator is 99.62%. The simulation results of two extreme cases and Monte Carlo show that the mismatch and PVT variations are restrained by the calibration circuit. Furthermore, it is promising to design a higher stage accumulator based on the proposed structure.

Key words: accumulator, signal-to-noise ratio (SNR), time delay integration (TDI), CMOS image sensor (CIS)



[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
Fig. 1.  The structure of the column parallel analog accumulator.

DownLoad: Full-Size Img PowerPoint
Fig. 2.  The timing diagram of the accumulator. (a) All the controlling clocks. (b) The details of the controlling clocks.

DownLoad: Full-Size Img PowerPoint
Fig. 3.  (a) The equivalent circuit during the first sampling phase. (b) The equivalent circuit during the holding phase.

DownLoad: Full-Size Img PowerPoint
Fig. 4.  The equivalent circuits of the i -th idle integrator.

DownLoad: Full-Size Img PowerPoint
Fig. 5.  (a) The equivalent circuits of the accumulator in the sampling phase considering the parasitics. (b) The equivalent circuits of the accumulator in the holding phase considering the parasitics.

DownLoad: Full-Size Img PowerPoint
Fig. 6.  Layout of one integrator of the accumulator.

DownLoad: Full-Size Img PowerPoint
Fig. 7.  The improved SNR versus the designed number of stage.

DownLoad: Full-Size Img PowerPoint
Fig. 8.  The i-th integrator with decoupling switch.

DownLoad: Full-Size Img PowerPoint
Fig. 9.  The improved timing diagram of the accumulator. (a) All the controlling clocks. (b) The details of the controlling clocks.

DownLoad: Full-Size Img PowerPoint
Fig. 10.  The equivalent circuits of the i -th idle integrator with decoupling switch.

DownLoad: Full-Size Img PowerPoint
Fig. 11.  Change in the i -th integrator.

DownLoad: Full-Size Img PowerPoint
Fig. 12.  The increased voltage after closing the top plate switch versus the output voltage of OPA.

DownLoad: Full-Size Img PowerPoint
Fig. 15.  Layout of the bootstrapped switch in an integrator.

DownLoad: Full-Size Img PowerPoint
Fig. 13.  The operation principle of the bootstrapped switch proposed (a) when the i-th integrator is in the integration phase and (b) when the i-th integrator is not in the integration phase.

DownLoad: Full-Size Img PowerPoint
Fig. 14.  The circuit of the bootstrapped voltage generator.

DownLoad: Full-Size Img PowerPoint
Fig. 16.  The increased voltage of the integrating capacitor in the top plate sampling versus the bootstrapped switch versus the output of OPA.

DownLoad: Full-Size Img PowerPoint
Fig. 17.  The correction circuit.

DownLoad: Full-Size Img PowerPoint
Fig. 18.  Layout of the correction circuit.

DownLoad: Full-Size Img PowerPoint
Fig. 19.  The output curves of the accumulators @ 6.4 mV.

DownLoad: Full-Size Img PowerPoint
Fig. 20.  Outputs of the accumulator with linearly inputs.

DownLoad: Full-Size Img PowerPoint
Fig. 21.  The curves of the output of accumulators versus the times of the accumulation for different calibration codes @ 6.4 mV.

DownLoad: Full-Size Img PowerPoint
Fig. 22.  Simulation results in two extreme cases. (a) Best fast case. (b) Worst slow case. (@ 6.4 mV).

DownLoad: Full-Size Img PowerPoint
Fig. 23.  Results of Monte Carlo simulation @ 6.4 mV.

DownLoad: Full-Size Img PowerPoint

Table 1.   The improved SNR for each calibration code.

DownLoad: CSV
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]

    • Search

    Advanced Search >>

    GET CITATION

    shu

    Export: BibTex EndNote

    Article Metrics

    Article views: 2922 Times PDF downloads: 32 Times Cited by: 0 Times

    History

    Received: 08 June 2015 Revised: Online: Published: 01 February 2016

    Catalog

      Email This Article

      User name:
      Email:*请输入正确邮箱
      Code:*验证码错误
      Send
      Article Navigation >  Journal of Semiconductors  > 2016  >  37(2): 025001
      Jianxin Li, Fujun Huang, Yong Zong, Jing Gao. High-stage analog accumulator for TDI CMOS image sensors[J]. Journal of Semiconductors, 2016, 37(2): 025001. doi: 10.1088/1674-4926/37/2/025001 ****J X Li, F J Huang, Y Zong, J Gao. High-stage analog accumulator for TDI CMOS image sensors[J]. J. Semicond., 2016, 37(2): 025001. doi: 10.1088/1674-4926/37/2/025001.
      Citation:
      Jianxin Li, Fujun Huang, Yong Zong, Jing Gao. High-stage analog accumulator for TDI CMOS image sensors[J]. Journal of Semiconductors, 2016, 37(2): 025001. doi: 10.1088/1674-4926/37/2/025001 ****
      J X Li, F J Huang, Y Zong, J Gao. High-stage analog accumulator for TDI CMOS image sensors[J]. J. Semicond., 2016, 37(2): 025001. doi: 10.1088/1674-4926/37/2/025001.
      shu

      High-stage analog accumulator for TDI CMOS image sensors

      DOI: 10.1088/1674-4926/37/2/025001

      • School of Electronic Information Engineering, Tianjin University, Tianjin 300072, China

      Funds:

      Project supported by the National Natural Science Foundation of China (Nos. 61404090, 61434004).

      More Information
      • Corresponding author: Email: gaojing@tju.edu.cn
      • Received Date: 2015-06-08
      • Accepted Date: 2015-09-01
      • Published Date: 2016-01-25

      Catalog

        Journal of Semiconductors © 2017 All Rights Reserved   京ICP备05085259号-2

        /

        DownLoad:  Full-Size Img  PowerPoint
        Return
        Return