| Citation: |
Yutian Wang, Chenguang Liu, Yuming Zhang. Progress of d0 magnetism in SiC[J]. Journal of Semiconductors, 2017, 38(3): 033006. doi: 10.1088/1674-4926/38/3/033006
****
Y T Wang, C G Liu, Y M Zhang. Progress of d0 magnetism in SiC[J]. J. Semicond., 2017, 38(3): 033006. doi: 10.1088/1674-4926/38/3/033006.
|
-
Abstract
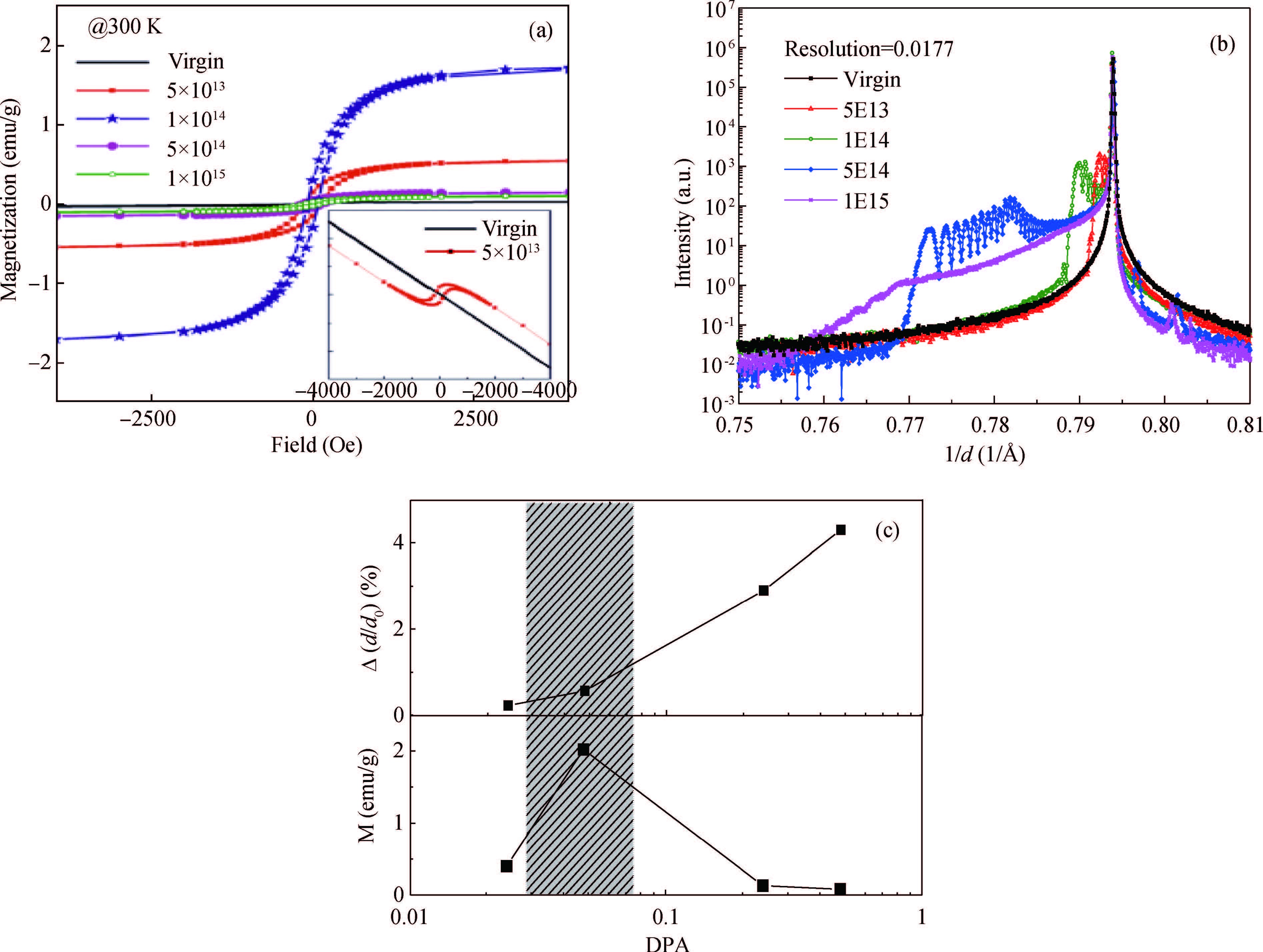
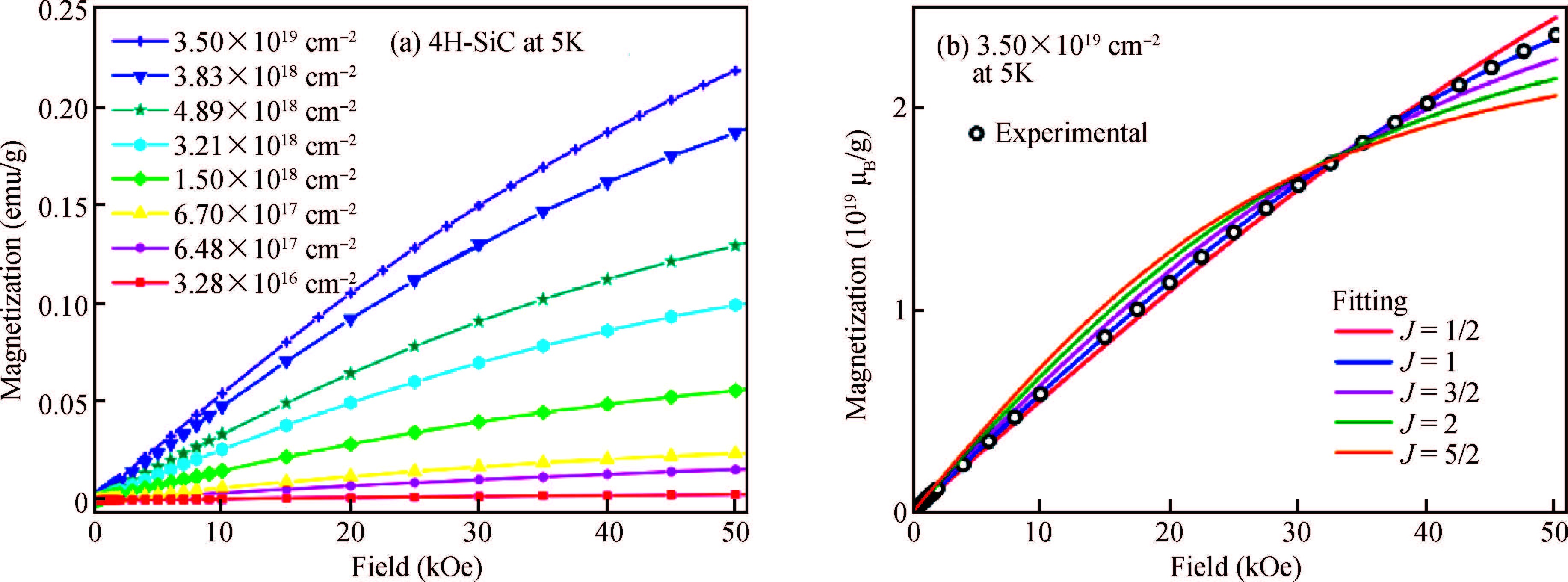
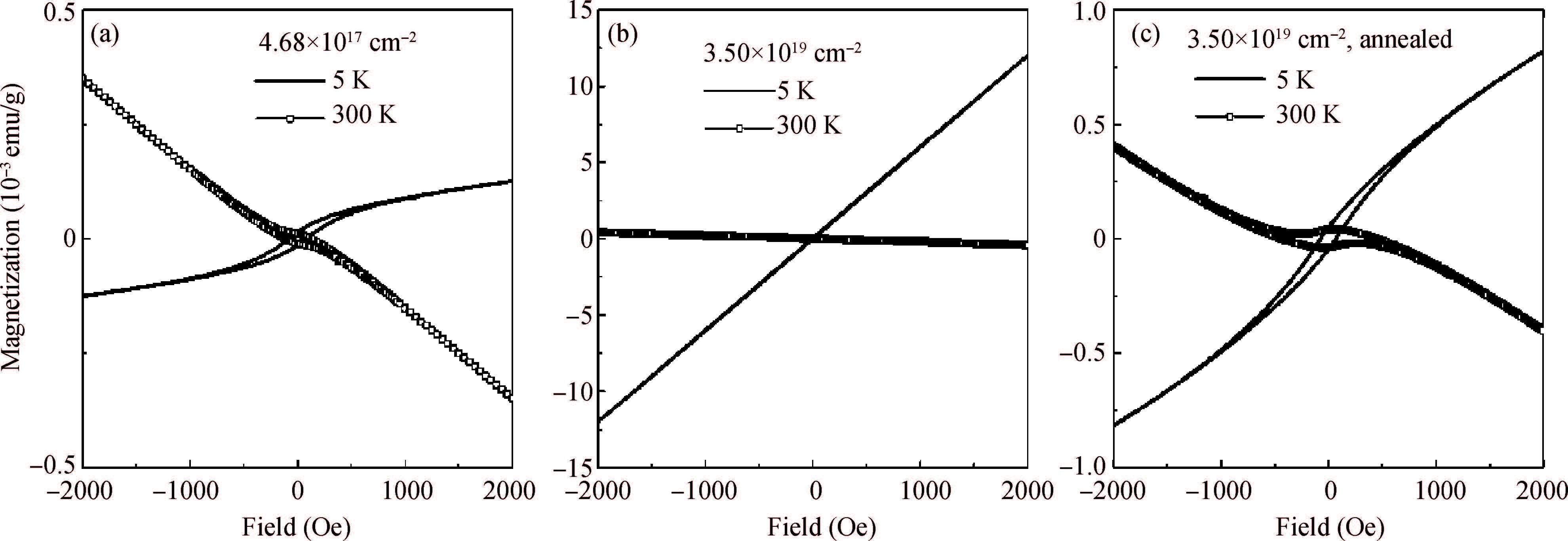
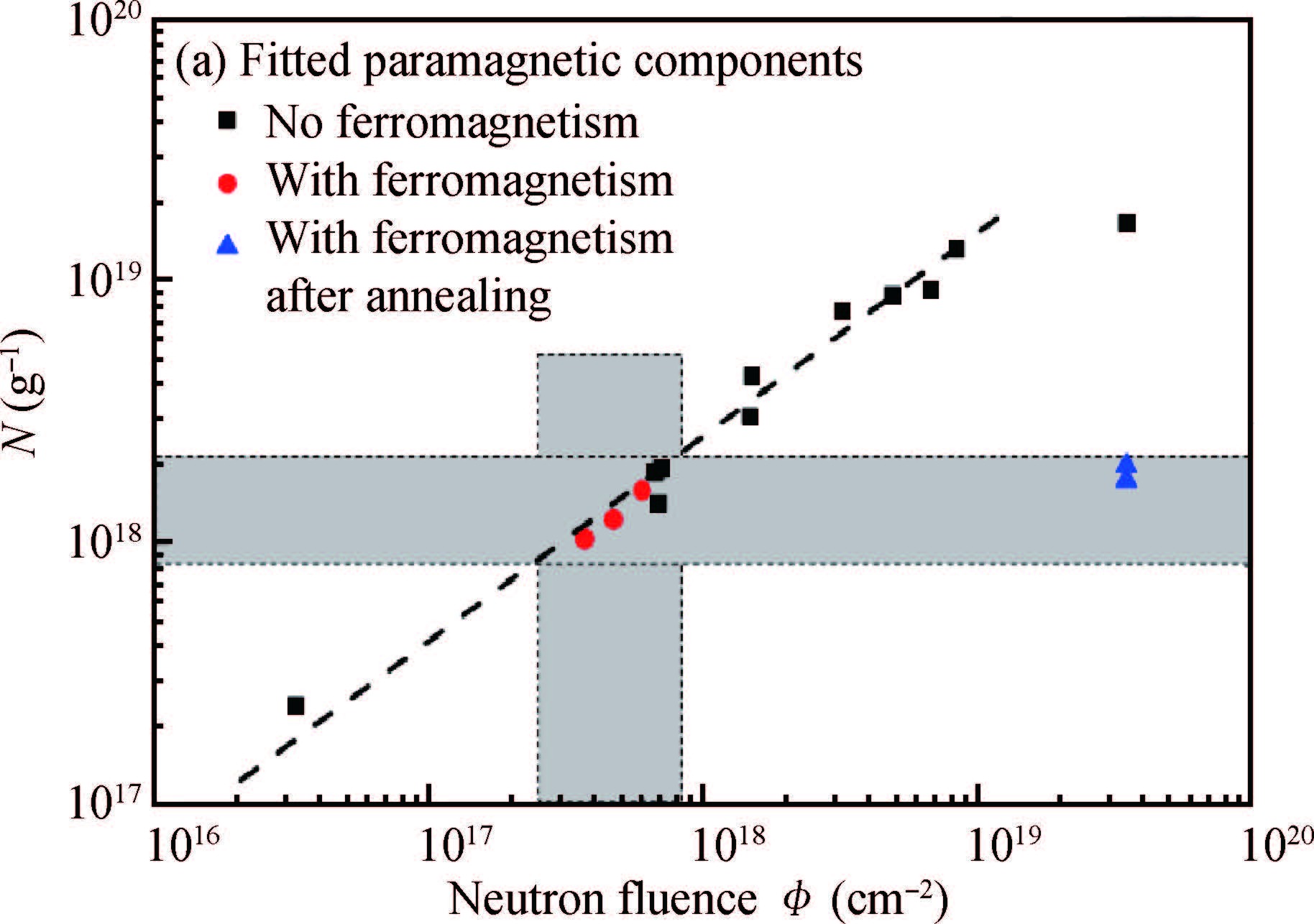
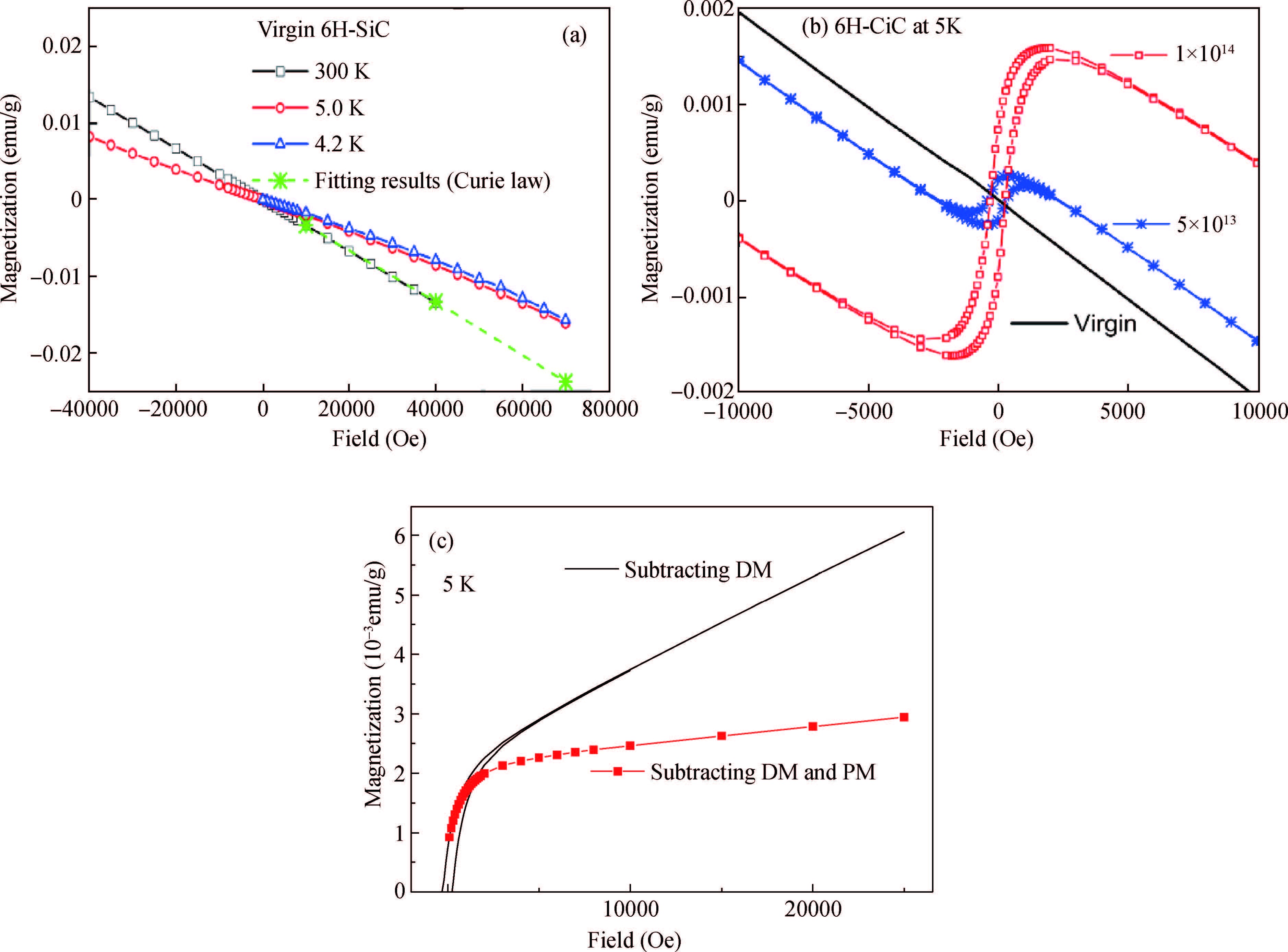
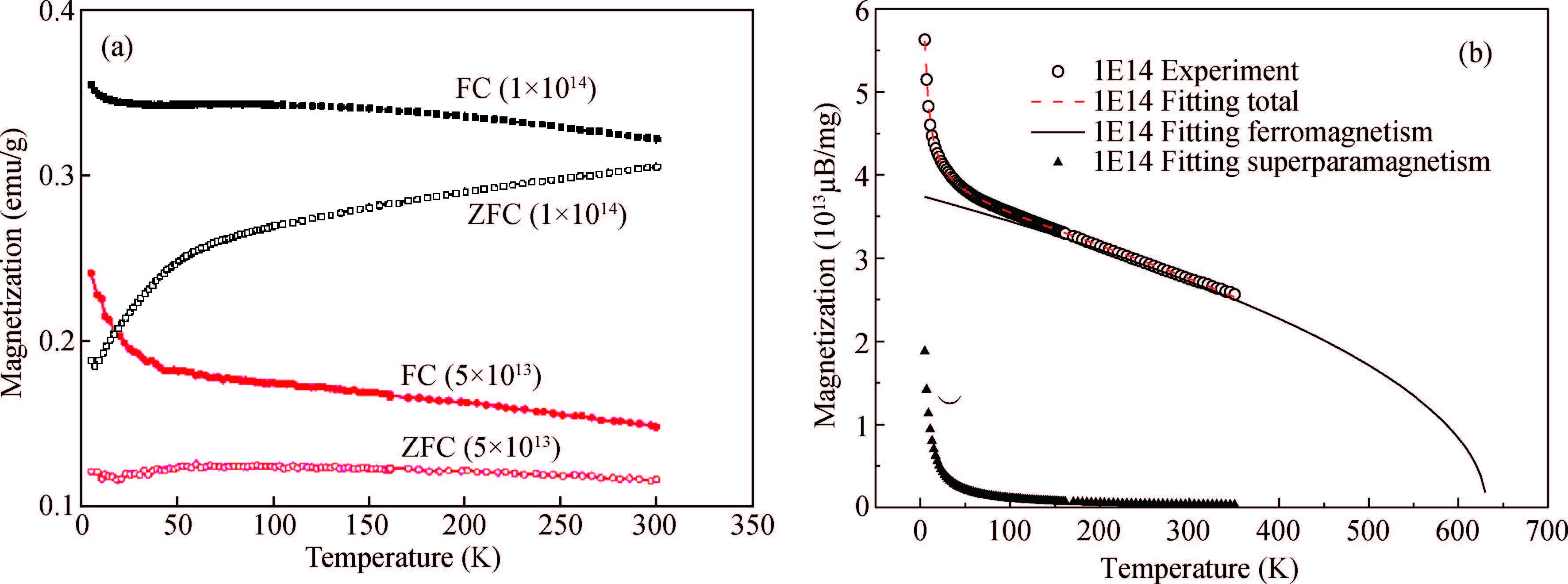
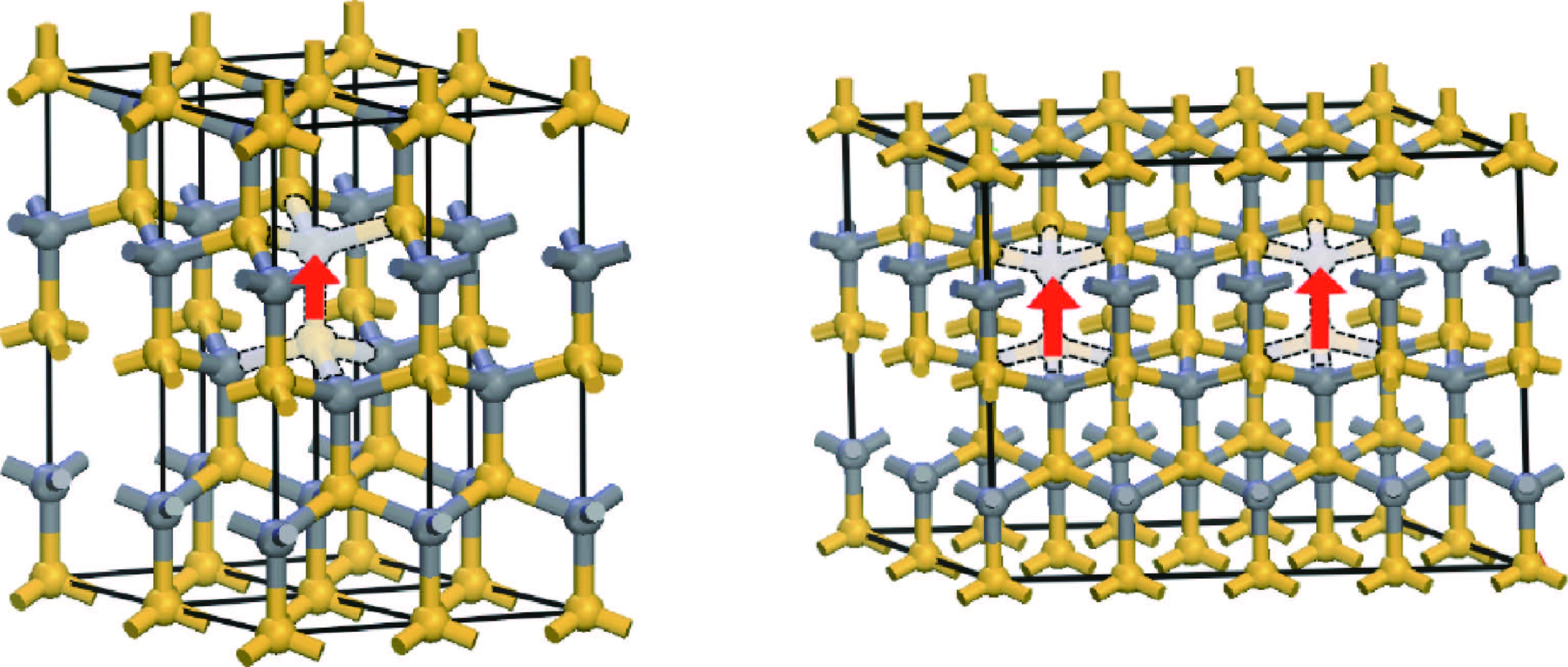
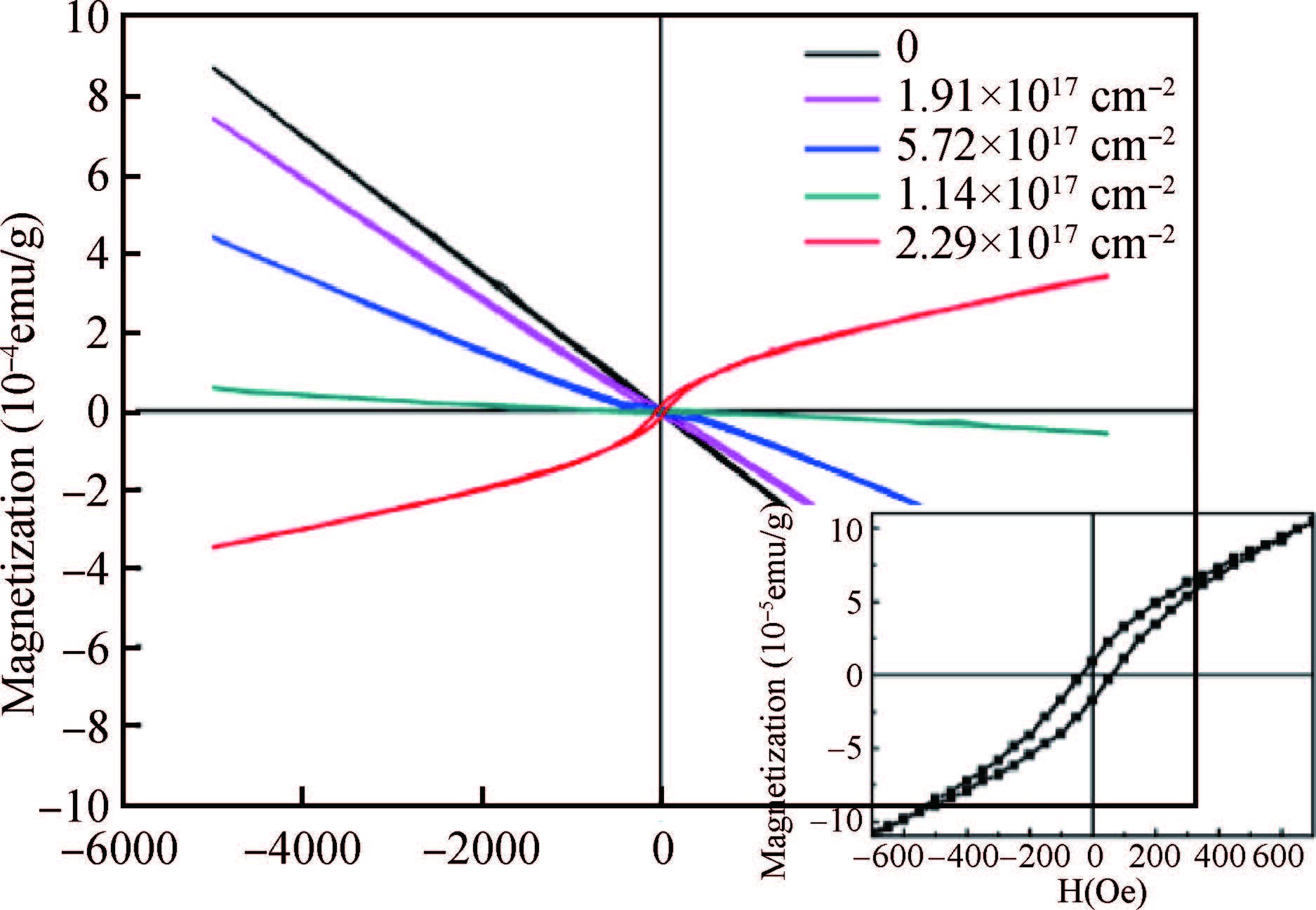
The properties of defect-induced ferromagnetism (d0 magnetism) in SiC belong to carbon-based material which has been systematically investigated after graphite. In this paper, we reviewed our research progress about d0 magnetism in two aspects, i.e., magnetic source and magnetic coupling mechanism. The VSiVC divacancies have been evidenced as the probable source of d0 magnetism in SiC. To trace the ferromagnetic source in microscopic and electronic view, the p electrons of the nearest-neighbor carbon atoms, which are around the VSiVC divacancies, are sourced. For magnetic coupling mechanism, a higher divacancy concentration leads to stronger paramagnetic interaction but not stronger ferromagnetic coupling. So the d0 magnetism can probably be explained as a local effect which is incapable of scaling up with the volume.-
Keywords:
- SiC,
- d0 magnetism,
- graphite
-
References
[1] Dietl T, Ohno H, Matsukura F. Hole-mediated ferromagnetism in tetrahedrally coordinated semiconductors. Phys Rev B, 2001, 63(19):195205 doi: 10.1103/PhysRevB.63.195205[2] Pearton S J, Lee K P, Overberg M E, et al. Magnetism in SiC implanted with high doses of Fe and Mn. J Electron Mater, 2002, 31(5):336 doi: 10.1007/s11664-002-0078-7[3] Venkatesan M, Fitzgerald C B, Coey J M D. Unexpected magnetism in a dielectric oxide. Nature, 2004, 430(7000):630 doi: 10.1038/430630a[4] Khalid M, Esquinazi P, Spemann D, et al. Hydrogen-mediated ferromagnetism in ZnO single crystals. New J Phys, 2011, 13(6):063017 doi: 10.1088/1367-2630/13/6/063017[5] Esquinazi P, Spemann D, Höne R, et al. Induced magnetic ordering by proton irradiation in graphite. Phys Rev Lett, 2003, 91(22):227201 doi: 10.1103/PhysRevLett.91.227201[6] Makarova T L, Han K H, Esquinazi P, et al. Magnetism in photopolymerized fullerenes. Carbon, 2003, 41(8):1575 doi: 10.1016/S0008-6223(03)00082-4[7] Dubman M, Shiroka T, Luetkens H, et al. Low-energy and SQUID evidence of magnetism in highly oriented pyrolytic graphite. J Magn Magn Mater, 2010, 322(9-12):1228 doi: 10.1016/j.jmmm.2009.04.023[8] Hebard A F, Rairigh R P, Kelly J G, et al. Mining for high Tc ferromagnetism in ion-implanted dilute magnetic semiconductors. J Phys D, 2004, 37(4):511 doi: 10.1088/0022-3727/37/4/001[9] Ma S B, Sun Y P, Zhao B C, et al. Magnetic properties of Mndoped cubic silicon carbide. Physica B, 2007, 394(1):122 doi: 10.1016/j.physb.2007.02.028[10] Zhang X H, Han J C, Zhou J G, et al. Ferromagnetism in homogeneous (Al,Co)-codoped 4H-silicon carbides. J Magn Magn Mater, 2014, 363(4):34[11] Kang C, Cai H, Zhang X, T et al. The study of high Curie temperature ferromagnetism properties in Mn-doped SiC thin film. Results Phys, 2015, 5:178 doi: 10.1016/j.rinp.2015.07.003[12] Ofuchi H, Wang W H, Takano F, et al. Fluorescence EXAFS analysis of SiC:Mn films synthesized on SiC substrates. Hedman B, Painetta P, editor, X-Ray Absorption Fine Structure-XAFS13, Melville:Amer Inst Physics, 2007:443 http://www.slac.stanford.edu/econf/C060709/papers/129_TUPO104.PDF[13] Bouziane K, Al Azri M, Elzain M, et al. Mn fraction substitutional site and defects induced magnetism in Mn-implanted 6HSiC. J Alloys Compd, 2015, 632:760 doi: 10.1016/j.jallcom.2015.01.275[14] Song B, Chen X L, Han J C, et al. Structural and magnetic properties of (Al, Fe)-codoped SiC. J Phys D, 2010, 43(41):1655[15] Miranda P, Wahl U, Catarino N, et al. Damage formation and recovery in Fe implanted 6H-SiC. Nucl Instrum Methods Phys Res, 2012, 286(9):89 http://adsabs.harvard.edu/abs/2012NIMPB.286...89M[16] Wang Y, Li L, Prucnal S, et al. Disentangling defect-induced ferromagnetism in SiC. Phys Rev B, 2014, 89(1):014417 doi: 10.1103/PhysRevB.89.014417[17] Esquinazi P, Hohn R. Magnetism in carbon structures. J Magn Magn Mater, 2005, 290:20[18] Coey J M D. Ferromagnetism. Solid State Sci, 2005, 7(6):660 doi: 10.1016/j.solidstatesciences.2004.11.012[19] Ohldag H, Esquinazi P, Arenholz E, et al. The role of hydrogen in room-temperature ferromagnetism at graphite surfaces. New J Phys, 2010, 12(12):123012 doi: 10.1088/1367-2630/12/12/123012[20] Nair R R, Sepioni M, Tsai I L. Spin-half paramagnetism in graphene induced by point defects. Nat Phys, 2012, 8:3 http://adsabs.harvard.edu/abs/2012NatPh...8..199N[21] Spemann D, Esquinazi P, Setzer A, et al. Trace element content and magnetic properties of commercial HOPG samples studied by ion beam microscopy and SQUID magnetometry. AIP Adv, 2014, 4(10):074211[22] Pan H, Yi J B, Shen L, et al. Room-temperature ferromagnetism in carbon-doped ZnO. Phys Rev Lett, 2007, 99(12):127201 doi: 10.1103/PhysRevLett.99.127201[23] Yi J B, Lim C C, Xing G Z, et al. Ferromagnetism in dilute magnetic semiconductors through defect engineering:Li-doped ZnO. Phys Rev Lett, 2010, 104(13):137201 doi: 10.1103/PhysRevLett.104.137201[24] Mathew S, Gopinadhan K, Chan T K, et al. Magnetism in MoS2 induced by proton irradiation. Appl Phys Lett, 2012, 101(10):102103 doi: 10.1063/1.4750237[25] Yan G, Zhang F, Niu Y, et al. Chloride-based fast homoepitaxial growth of 4H-SiC films in a vertical hot-wall CVD. J Semicond, 2016, 37(6):063001 doi: 10.1088/1674-4926/37/6/063001[26] Jantawongrit P, Sanorpim S, Yaguchi H, et al. Microstructures of InN film on 4H-SiC (0001) substrate grown by RF-MBE. J Semicond, 2015, 36(8):37 http://adsabs.harvard.edu/abs/2015JSemi..36h3002J[27] Zhuo S Y, Liu X, Liu X, et al. Recent progress in research of fSiC codoped with N-B-Al pairs for optoelectronics. J Semicond, 2015, 36(8):083003 doi: 10.1088/1674-4926/36/8/083003[28] Jenny J R, Malta D P, Muller S G, et al. High-purity semiinsulating 4H-SiC for microwave device applications. J Electron Mater, 2003, 32(5):432 doi: 10.1007/s11664-003-0173-4[29] Liu Y, Wang G, Wang S, et al. Defect-induced magnetism in neutron irradiated 6H-SiC single crystals. Phys Rev Lett, 2011, 106(8):087205 doi: 10.1103/PhysRevLett.106.087205[30] Li L. Rise and fall of defect induced ferromagnetism in SiC single crystals. Appl Phys Lett, 2011, 98(22):222508 doi: 10.1063/1.3597629[31] Brauer G, Anwand W, Coleman P G, et al. Positron studies of defects in ion-implanted SiC. Phys Rev B, 1996, 54(5):3084 doi: 10.1103/PhysRevB.54.3084[32] Zhou R W, Liu X C, Zhuo S Y, et al. Divacancies induced ferromagnetism in 3C-SiC thin films. J Magn Magn Mater, 2015, 374:559 doi: 10.1016/j.jmmm.2014.08.081[33] Zhou R W, Liu X C, Li F, et al. Defects induced ferromagnetism in hydrogen irradiated 3C-SiC thin films. Mater Lett, 2015, 156:54 doi: 10.1016/j.matlet.2015.04.143[34] Son N T, Carlsson P, Ul Hassan J, et al. Defects and carrier compensation in semi-insulating 4H-SiC substrates. Phys Rev B, 2007, 75(15):155204 doi: 10.1103/PhysRevB.75.155204[35] Torpo L, Staab T E M, Nieminen R M. Divacancy in 3C- and 4H-SiC:an extremely stable defect. Phys Rev B, 2002, 65(8):5202 https://www.researchgate.net/publication/235584679_Divacancy_in_3C-and_4H-SiC_An_extremely_stable_defect[36] Gali A, Bockstedte M, Son N T, et al. Divacancy and its identification:theory. Devaty R P, editor, Silicon Carbide and Related Materials 2005, Pts 1 and 2, 2006:523[37] Zhu C Y, Ling C C, Brauer G, et al. Vacancy-type defects in 6H silicon carbide induced by He-implantation:a positron annihilation spectroscopy approach. J Phys D, 2008, 41(19):3080[38] Carlos W E, Garces N Y, Glaser E R, et al. Annealing of multivacancy defects in 4H-SiC. Phys Rev B, 2006, 74(23):235201 doi: 10.1103/PhysRevB.74.235201[39] Piamonteze C, Miedema P, De Groot F M F. Accuracy of the spin sum rule in XMCD for the transition-metal L edges from manganese to copper. Phys Rev B, 2009, 80(18):184410 doi: 10.1103/PhysRevB.80.184410[40] Schüz G, Wagner W, Wilhelm W, et al. Absorption of circularly polarized x rays in iron. Phys Rev Lett, 1987, 58(7):737 doi: 10.1103/PhysRevLett.58.737[41] Thole B T, Carra P, Sette F, et al. X-ray circular dichroism as a probe of orbital magnetization. Phys Rev Lett, 1992, 68(12):1943 doi: 10.1103/PhysRevLett.68.1943[42] Stohr J, Wu Y, Hermsmeier B D, et al. Element-specific mag netic microscopy with circularly polarized x-rays. Science, 1993, 259(259):658[43] Wang Y T, Liu Y, Wang G, et al. Carbon p electron ferromag netism in silicon carbide. Scientific Reports, 2015, 5:8999 doi: 10.1038/srep08999[44] Brüwiler P A, Maxwell A J, Puglia C, et al. π* and σ* excitons in C 1 s absorption of graphite. Phys Rev Lett, 1995, 74(4):614 doi: 10.1103/PhysRevLett.74.614[45] Wang Y, Chen X, Li L, et al. Structural and magnetic properties of irradiated SiC. J Appl Phys, 2014, 115(17):596 https://www.researchgate.net/profile/Xuliang_Chen/publication/259743074_Structural_and_magnetic_properties_of_irradiated_SiC/links/0c96052d76ec4d58f9000000.pdf?inViewer=0&pdfJsDownload=0&origin=publication_detail[46] Heinisch H L, Greenwood L R, Weber W J, et al. Displacement damage in silicon carbide irradiated in fission reactors. J Nucl Mater, 2004, 327(2/3):175[47] Wang Y, Liu Y, Wendler E, et al. Defect-induced magnetism in SiC:interplay between ferromagnetism and paramagnetism. Phys Rev B, 2015, 92(17):174409 doi: 10.1103/PhysRevB.92.174409[48] He X J, Tan J, Zhang B L, et al. Irradiation-induced magnetic ordering in SiC:experimental results and a density functional study. Appl Phys Lett, 2013, 103(26):262409 doi: 10.1063/1.4860957[49] Zheng H W, Yan Y L, Lv Z C, et al. Room-temperature ferromag netism in Cu-implanted 6H-SiC single crystal. Appl Phys Lett, 2013, 102(14):142409 doi: 10.1063/1.4800562[50] Lv Z C, Ma X P, Zheng H W, et al. Room temperature ferromag netism induced by N-ion implantation in 6H-SiC single crystal. Mater Lett, 2013, 93:374 doi: 10.1016/j.matlet.2012.11.118[51] Xu B, Yin J, Xia Y D, et al. Ferromagnetic and antiferromagnetic properties of the semihydrogenated SiC sheet. Appl Phys Lett, 2010, 96(14):143111 doi: 10.1063/1.3379025[52] Zhang Y J, Qin H W, Cao E S, et al. Ferromagnetism induced by intrinsic defects and boron substitution in single-wall SiC nano tubes. J Phys Chem A, 2011, 115(35):9987 doi: 10.1021/jp109470r[53] G Mishra, S Mishra, S Prusty, et al. Magnetic properties of nanocrystalline beta-SiC. J Nanosci Nanotechnol, 2011, 11(6):5049 doi: 10.1166/jnn.2011.4109 -
Proportional views





 DownLoad:
DownLoad: