| Citation: |
Hongzhen Fang, Pengjun Wang, Xu Cheng, Keji Zhou. High speed true random number generator with a new structure of coarse-tuning PDL in FPGA[J]. Journal of Semiconductors, 2018, 39(3): 035001. doi: 10.1088/1674-4926/39/3/035001
****
H Z Fang, P J Wang, X Cheng, K J Zhou. High speed true random number generator with a new structure of coarse-tuning PDL in FPGA[J]. J. Semicond., 2018, 39(3): 035001. doi: 10.1088/1674-4926/39/3/035001.
|
High speed true random number generator with a new structure of coarse-tuning PDL in FPGA
DOI: 10.1088/1674-4926/39/3/035001
More Information
-
Abstract
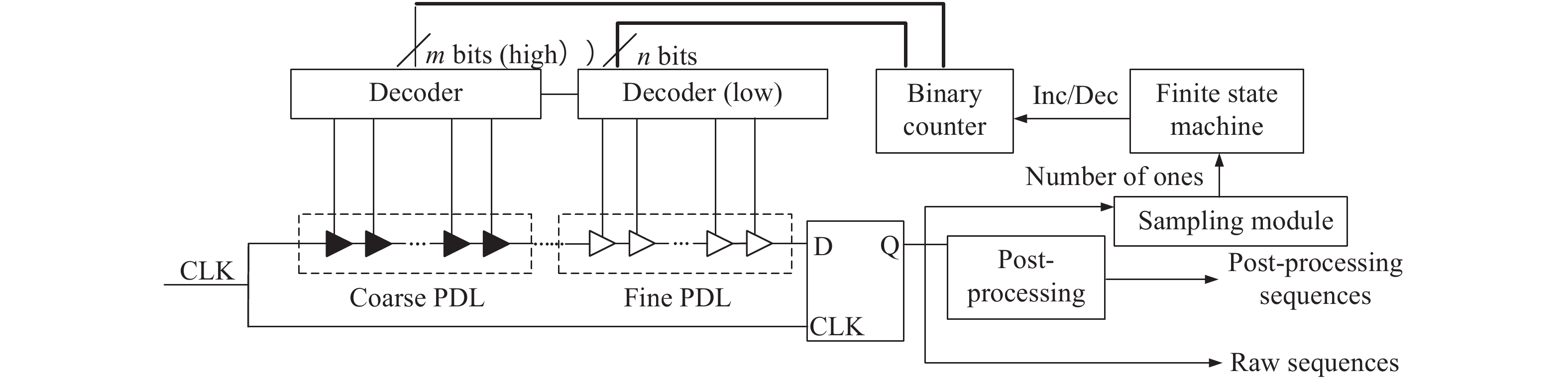
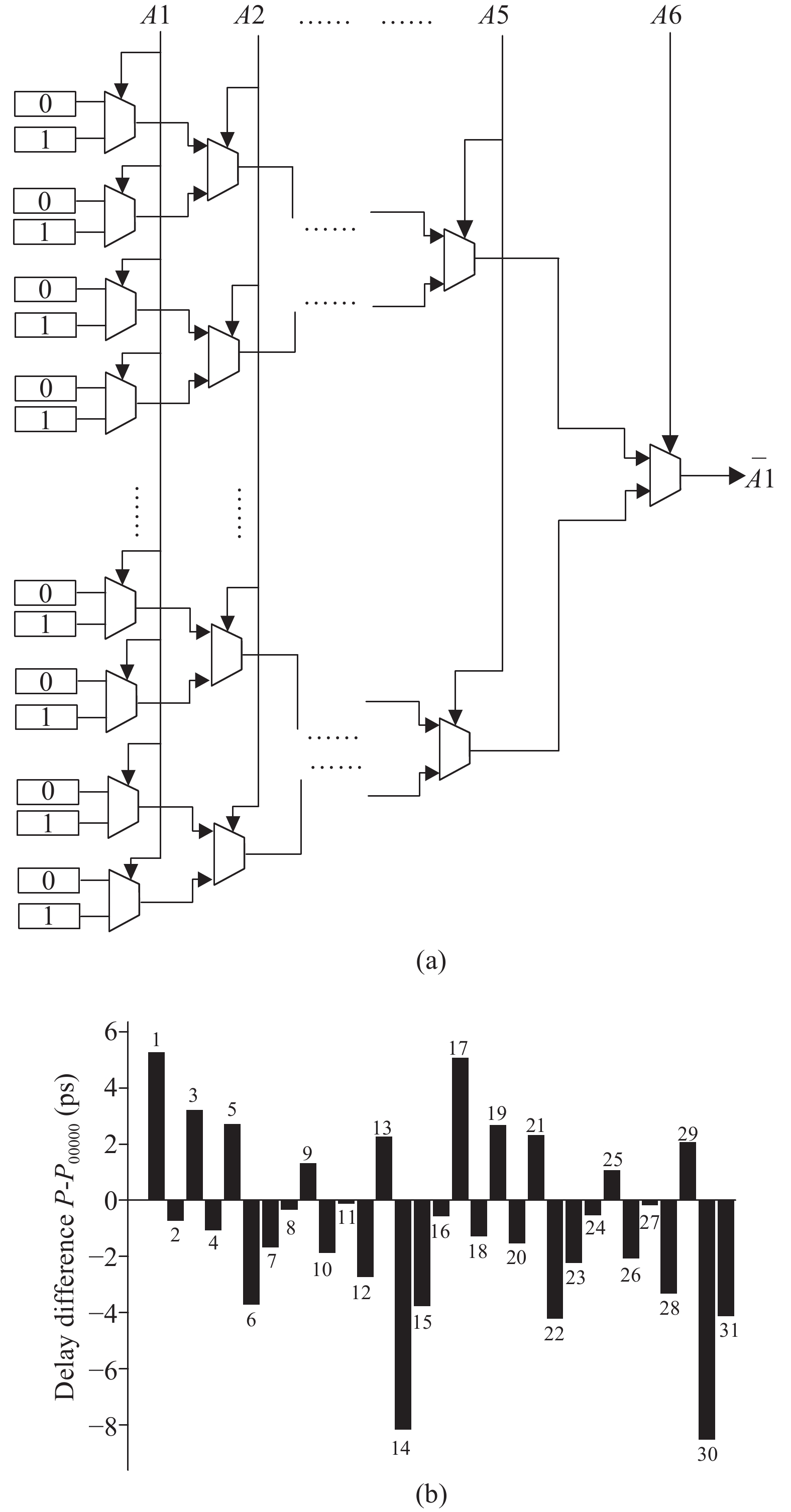
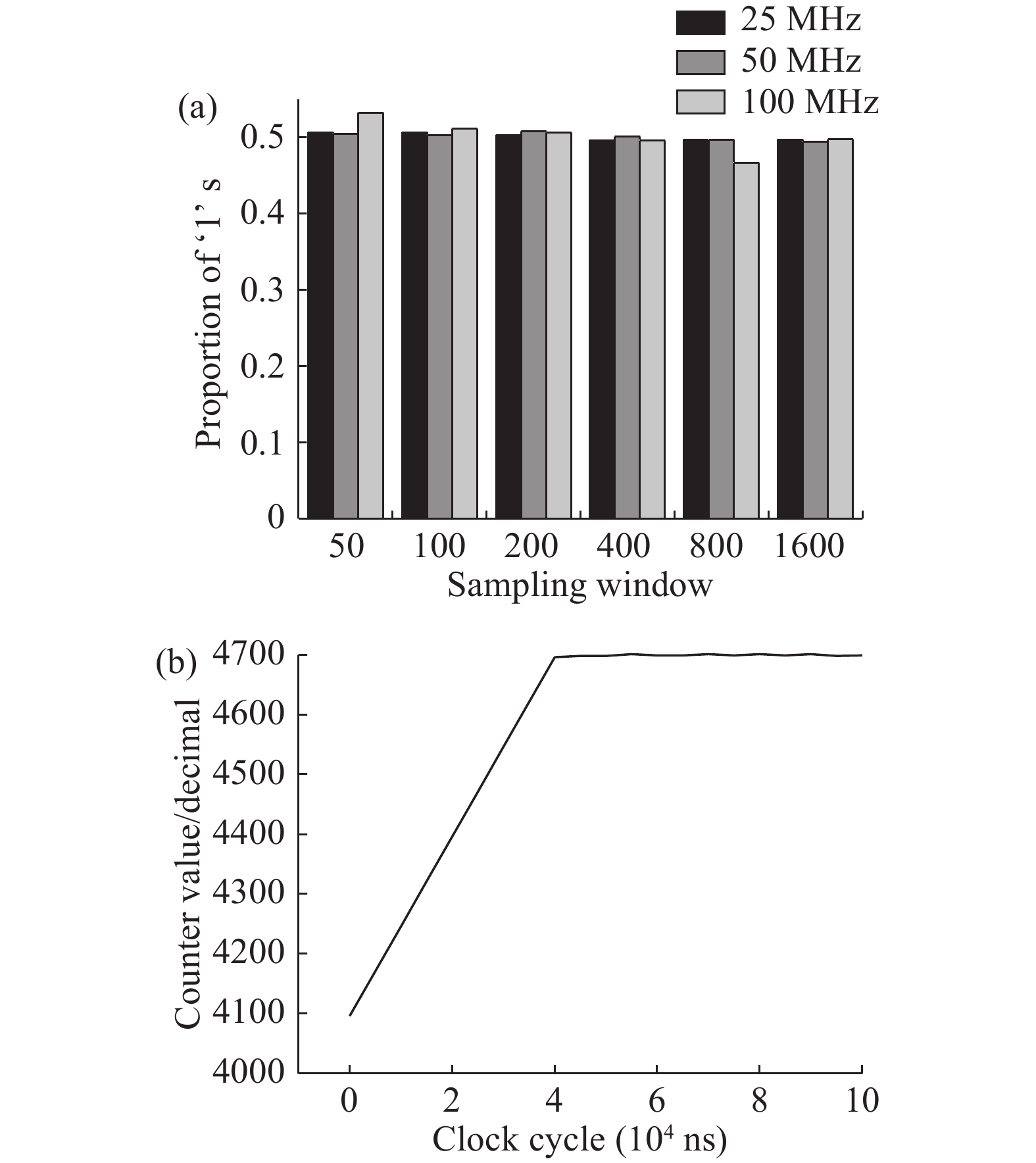
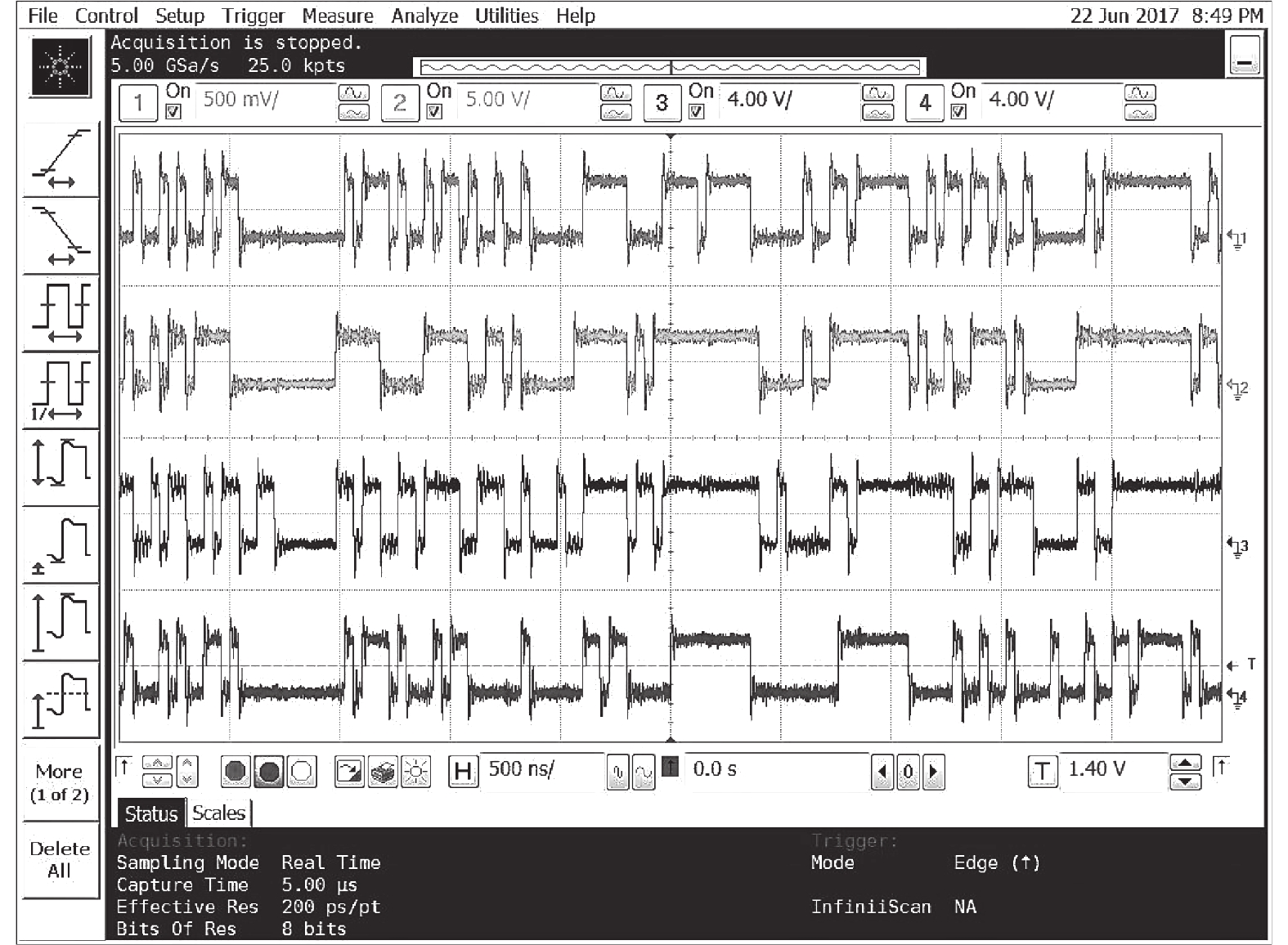
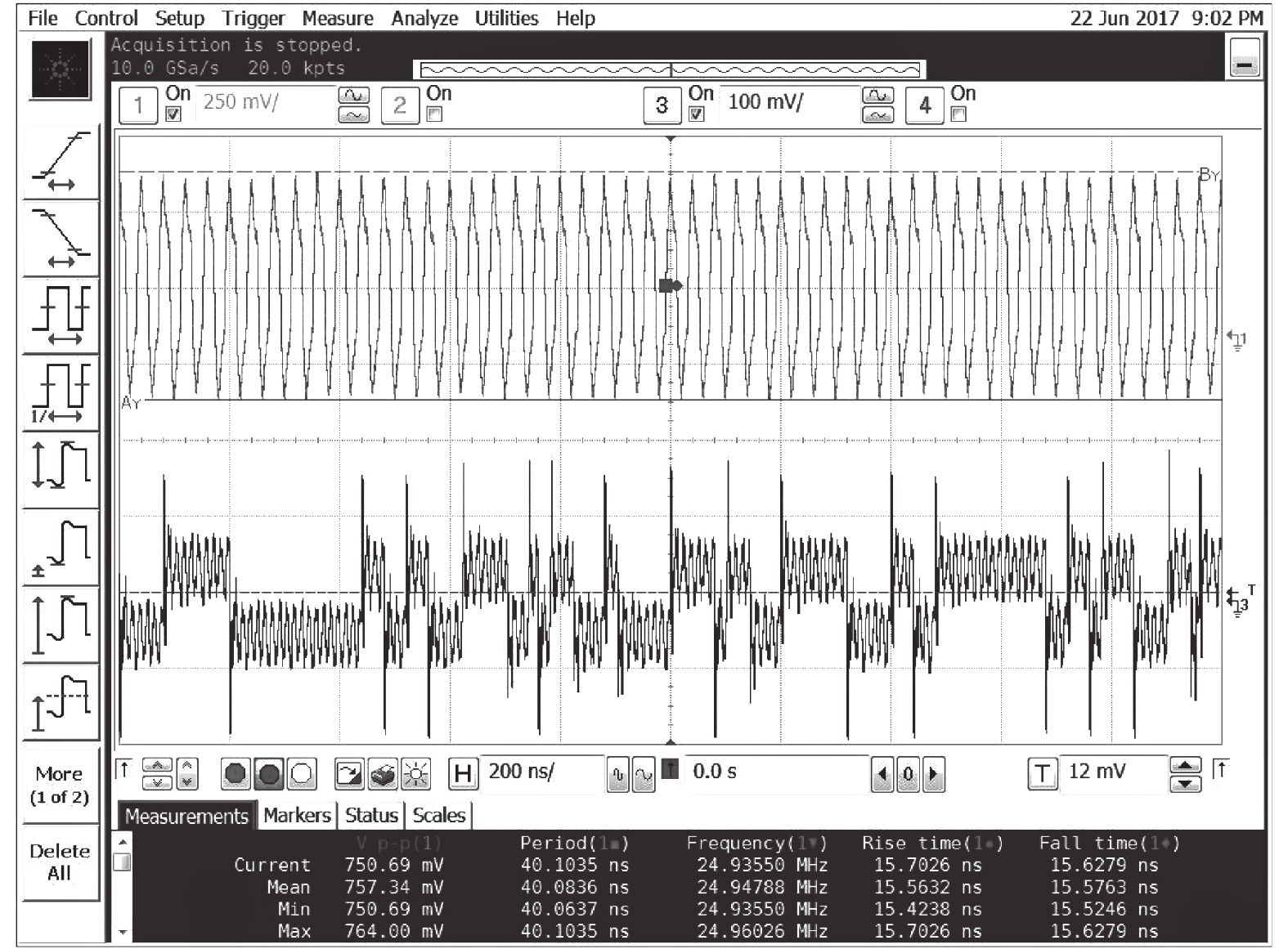
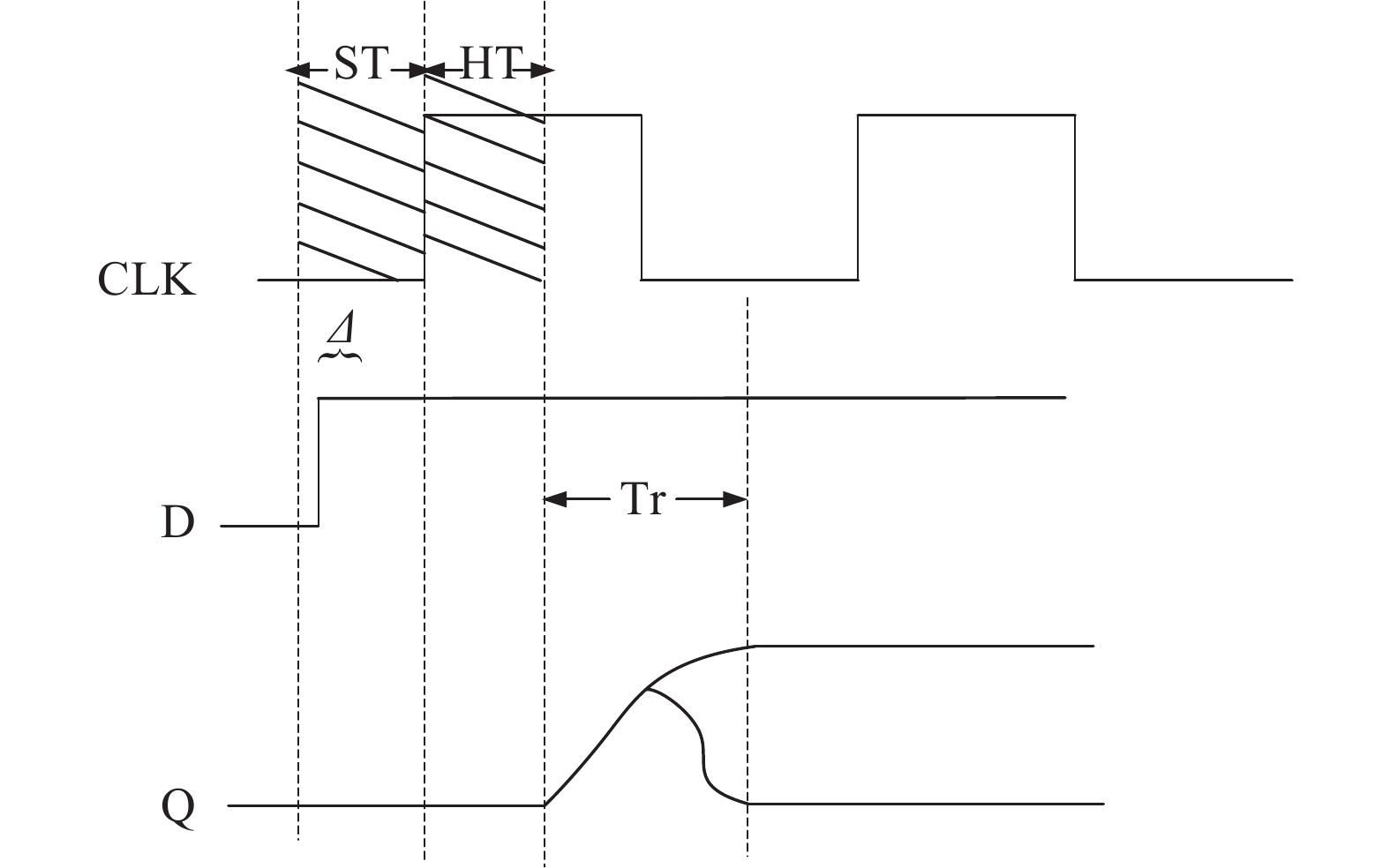
A metastability-based TRNG (true random number generator) is presented in this paper, and implemented in FPGA. The metastable state of a D flip-flop is tunable through a two-stage PDL (programmable delay line). With the proposed coarse-tuning PDL structure, the TRNG core does not require extra placement and routing to ensure its entropy. Furthermore, the core needs fewer stages of coarse-tuning PDL at higher operating frequency, and thus saves more resources in FPGA. The designed TRNG achieves 25 Mbps @ 100 MHz throughput after proper post-processing, which is several times higher than other previous TRNGs based on FPGA. Moreover, the robustness of the system is enhanced with the adoption of a feedback system. The quality of the designed TRNG is verified by NIST (National Institute of Standards and Technology) and also accepted by class P1 of the AIS-20/31 test suite.-
Keywords:
- TRNG,
- FPGA,
- metastability-based,
- coarse-tuning PDL
-
References
[1] Drutarovsky M, Galajda P. A robust chaos-based true random number generator embedded in reconfigurable switched-capacitor hardware. 17th International Conference on Radioelektronika, 2007: 1[2] Simka M, Drutarovsky M, Fischer V, et al. Model of a true random number generator aimed at cryptographic applications. IEEE International Symposium on Circuits and Systems, 2006: 5619[3] Zhou T, Zhou Z B, Yu M Y, et al. A robust low power chaos-based truly random number generator. Chin J Semicond, 2008, 29(1): 69 (in Chinese)[4] Liu Y, Cheung R C C, Wong H. A bias-bounded digital true random number generator architecture. IEEE Trans Circuits Syst I, 2017, 64(1): 133 doi: 10.1109/TCSI.2016.2606353[5] Petrie C S, Connelly J A. A noise-based IC random number generator for applications in cryptography. IEEE Trans Circuits Syst I, 2000, 47(5): 615 doi: 10.1109/81.847868[6] Mathew S K, Johnston D, Satpathy S, et al. uRNG: A 300–950 mV, 323 Gbps/W all-digital full-entropy true random number generator in 14 nm FinFET CMOS. IEEE J Solid-State Circuits, 2016, 51(7): 1695 doi: 10.1109/JSSC.2016.2558490[7] Johnson A P, Rajat S C, Debdeep M. An improved DCM-based tunable true random number generator for Xilinx FPGA. IEEE Trans Circuits Syst II, 2017, 64(4): 452 doi: 10.1109/TCSII.2016.2566262[8] Wieczorek P Z, Golofit K. Dual-metastability time-competitive true random number generator. IEEE Transn Circuits Syst I, 2014, 61(1): 134 doi: 10.1109/TCSI.2013.2265952[9] Wieczorek P Z. An FPGA implementation of the resolve time-based true random number generator with quality control. IEEE Trans Circuits Syst I, 2014, 61(12): 3450 doi: 10.1109/TCSI.2014.2338615[10] Hisashi H, Ichikawa S. FPGA implementation of metastability-based true random number generator. IEICE Trans Inform Syst, 2012, 95(2): 426[11] Majzoobi M, Koushanfar F, Devadas S. FPGA-based true random number generation using circuit metastability with adaptive feedback control. International Workshop on Cryptographic Hardware and Embedded Systems. Berlin: Springer, 2011: 17[12] Figueiredo P M. Comparator metastability in the presence of noise. IEEE Trans Circuits Syst I, 2013, 60(5): 1286 doi: 10.1109/TCSI.2012.2221195[13] Ou H W, Zhao J, Li Q R. Post-processing method in truly random number generator. Comput Sci, 2012, 39(B06): 9[14] Tsuneda A, Sugahara T, Inoue T. Statistical properties of modulo-2 added binary sequences. IEICE Trans Fundam Electron, Commun Comput Sci, 2004, 87(9): 2267[15] Danger J L, Guilley S, Hoogvorst P. Fast true random generator in FPGAs. IEEE Northeast Workshop on Circuits and Systems, 2007: 506[16] Varchola M, Drutarovsky M. New high entropy element for FPGA based true random number generators. International Workshop on Cryptographic Hardware and Embedded Systems. Berlin: Springer, 2010: 351[17] Xu X, Wang Y. High speed true random number generator based on FPGA. International Conference on Information Systems Engineering (ICISE) Conference, 2016: 18[18] Rozic V, Yang B, Dehaene W, et al. Highly efficient entropy extraction for true random number generators on FPGAs. 52nd ACM/EDAC/IEEE Design Automation Conference (DAC), 2015: 1[19] Bae S G, Kim Y, Park Y, et al. 3-Gb/s high-speed true random number generator using common-mode operating comparator and sampling uncertainty of D flip-flop. IEEE J Solid-State Circuits, 2017, 52(2): 605 doi: 10.1109/JSSC.2016.2625341[20] Peng, Y M, Zhao H B, Sun X, et al. A side-channel attack resistant AES with 500 Mbps, 1.92 pJ/bit PVT variation tolerant true random number generator. IEEE Computer Society Annual Symposium on VLSI, 2017: 249 -
Proportional views





 DownLoad:
DownLoad: