Fig. 1.
(Color online) The structure of defect-free and charged states of a-SiO2: white, red and yellow balls represent hydrogen, oxygen and silica atoms, respectively.
DownLoad:
| Citation: |
Dahua Ren, Baoyan Xiang, Cheng Hu, Kai Qian, Xinlu Cheng. The electronic and optical properties of amorphous silica with hydrogen defects by ab initio calculations[J]. Journal of Semiconductors, 2018, 39(4): 042002. doi: 10.1088/1674-4926/39/4/042002
****
D H Ren, B Y Xiang, C Hu, K Qian, X L Cheng. The electronic and optical properties of amorphous silica with hydrogen defects by ab initio calculations[J]. J. Semicond., 2018, 39(4): 042002. doi: 10.1088/1674-4926/39/4/042002.
|
The electronic and optical properties of amorphous silica with hydrogen defects by ab initio calculations
doi: 10.1088/1674-4926/39/4/042002
More Information-
Abstract
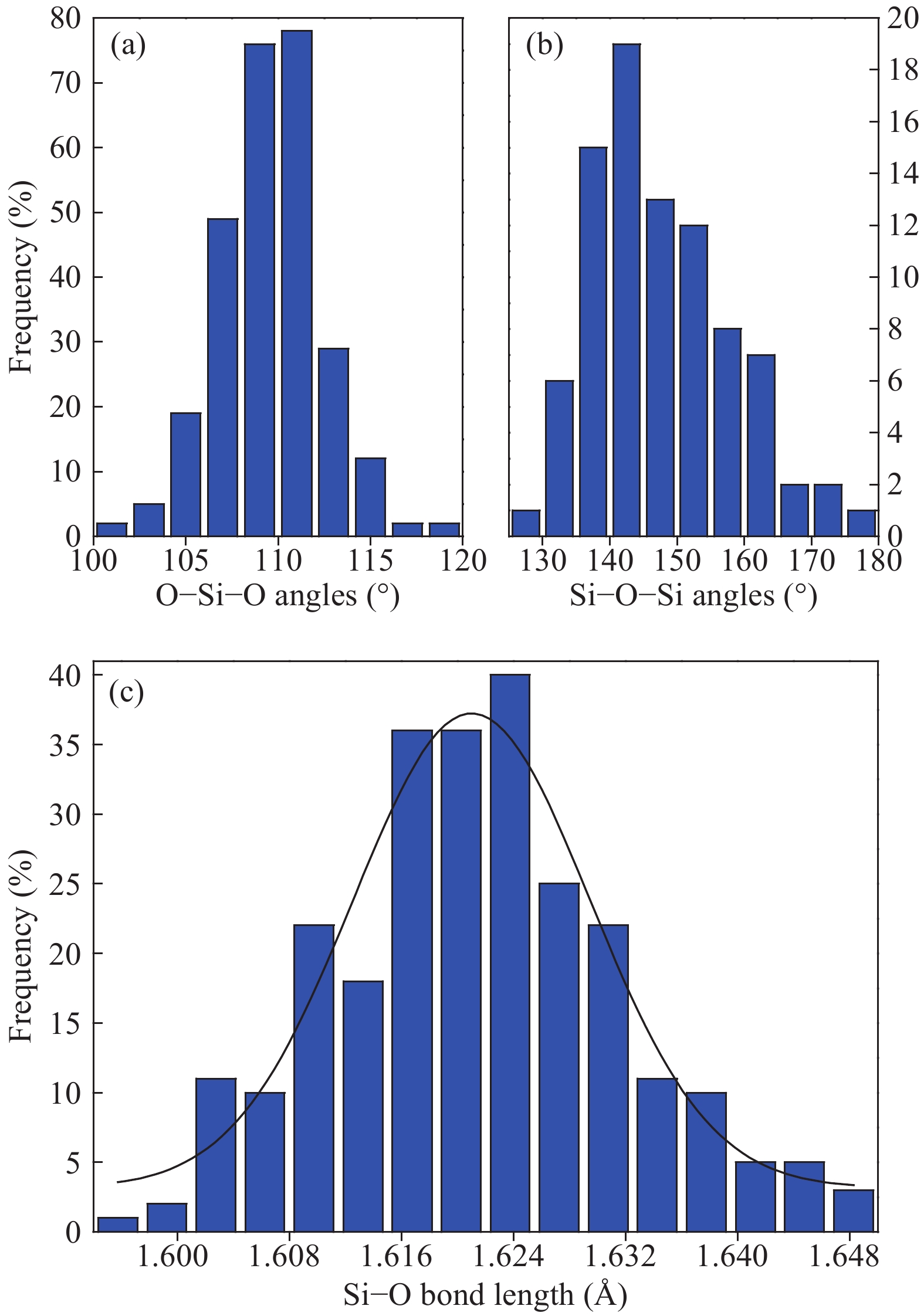
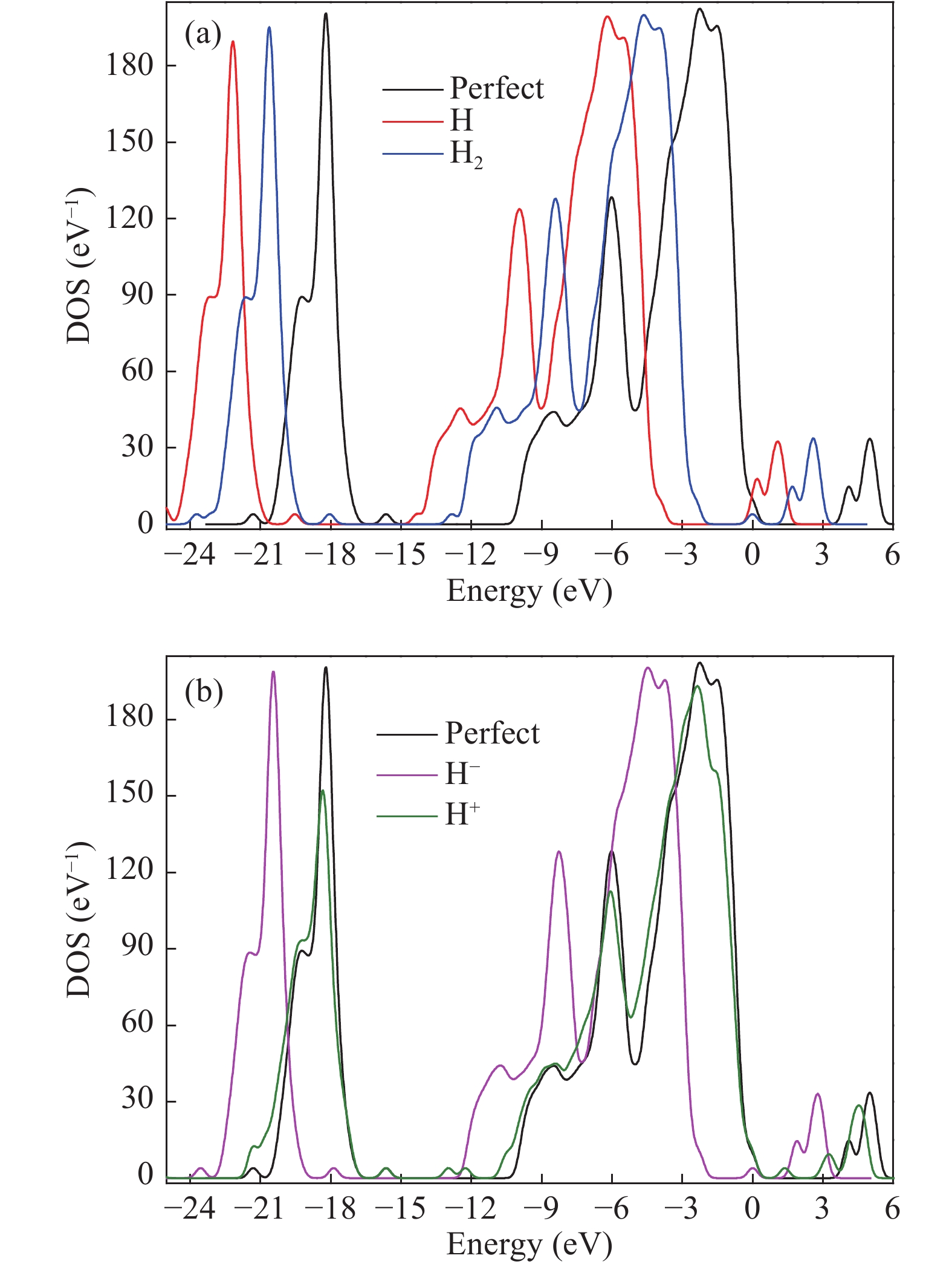
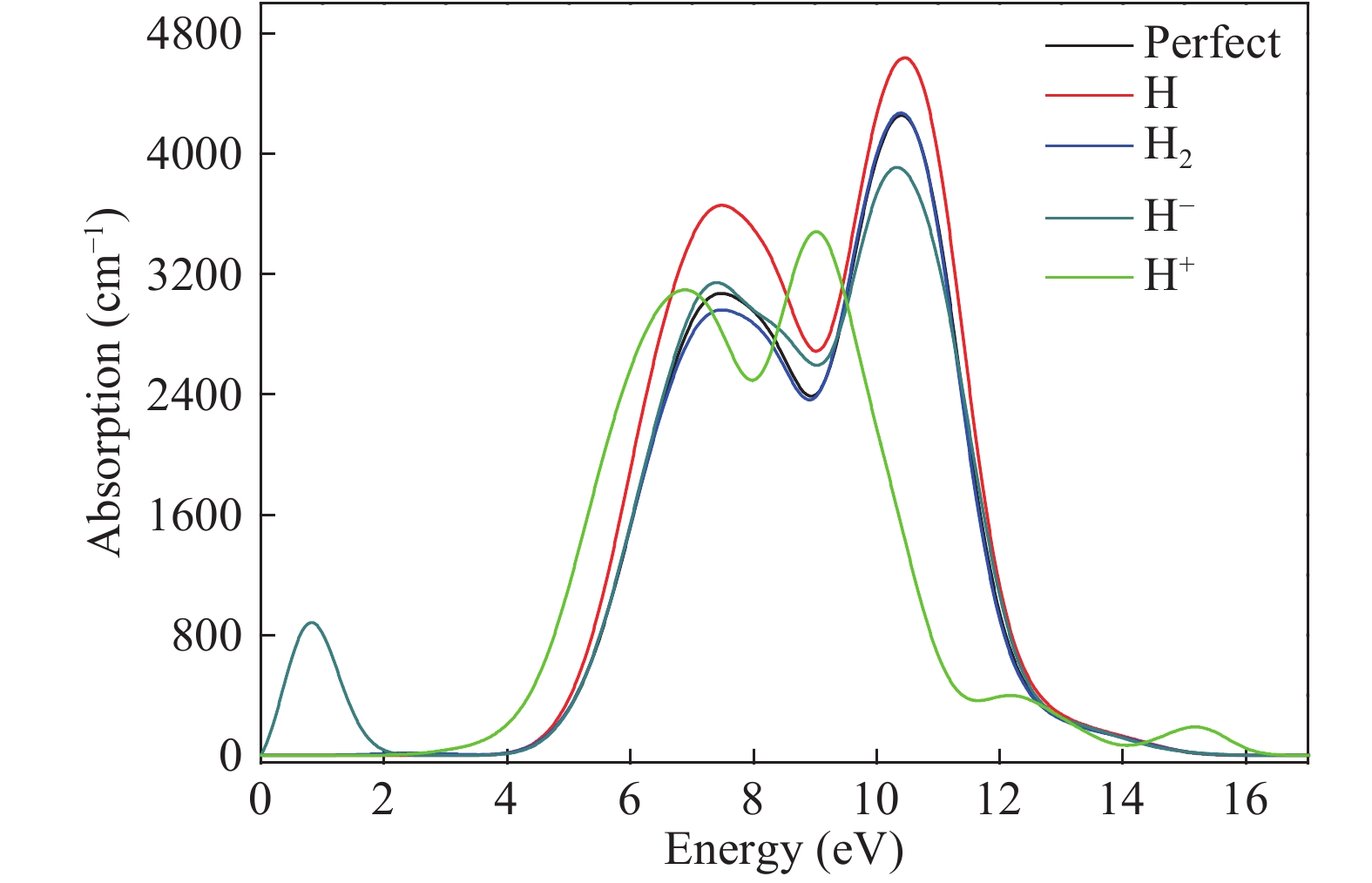
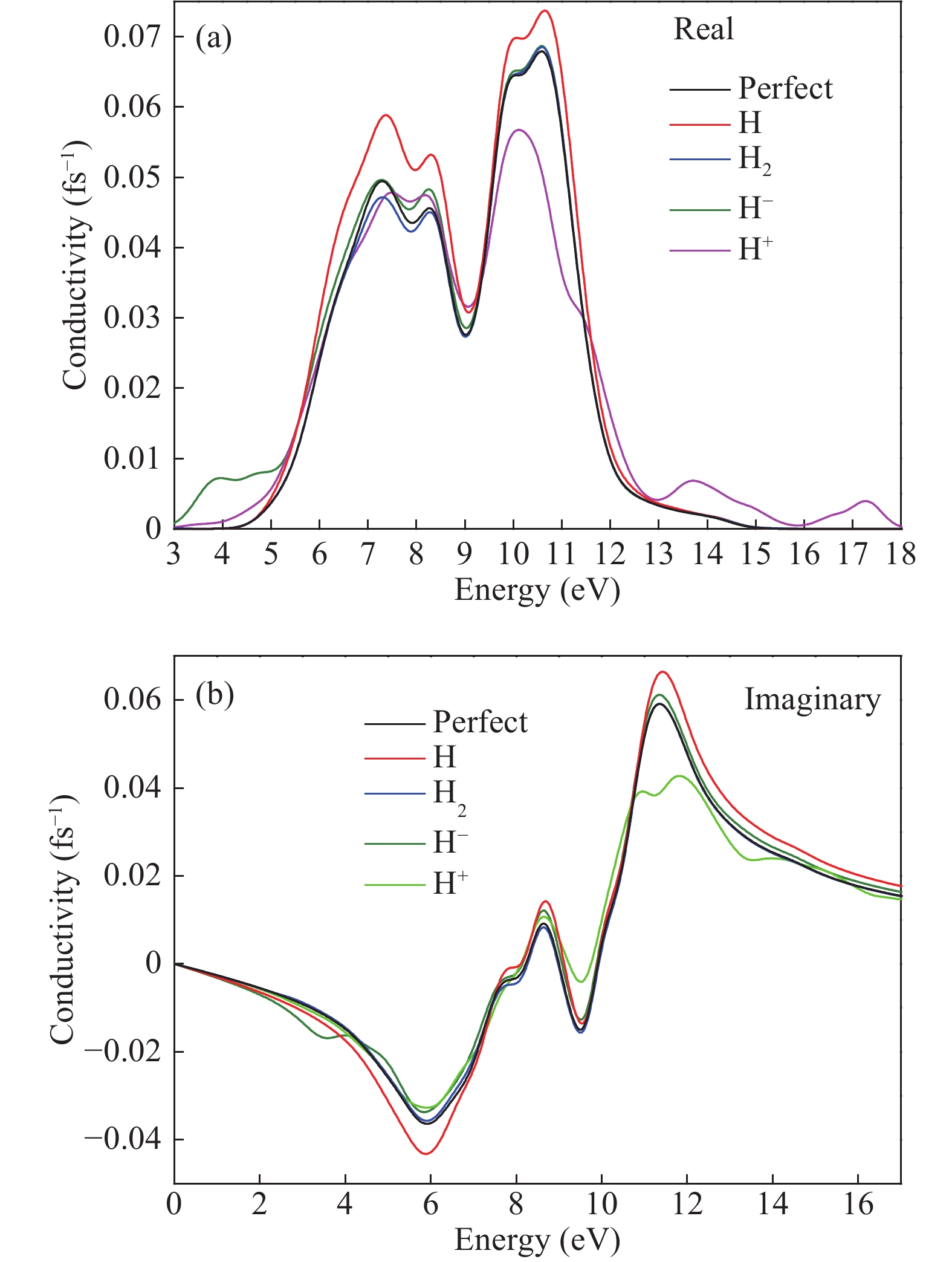
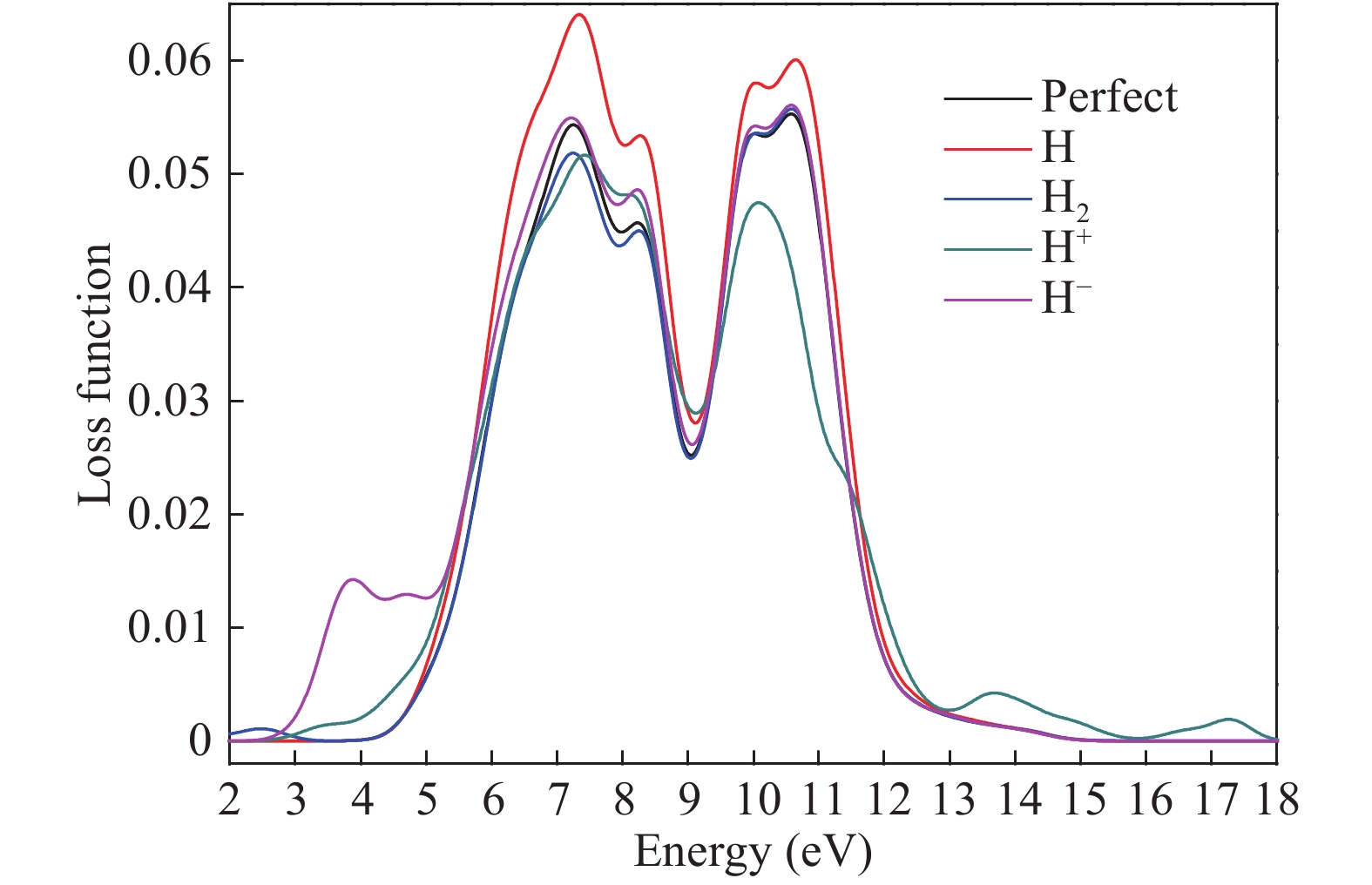
Hydrogen can be trapped in the bulk materials in four forms: interstitial molecular H2, interstitial atom H, O−H+(2Si=O–H)+, Si−H−(${\rm{4O}}\bar \equiv {\rm{Si−H}}$ )− to affect the electronic and optical properties of amorphous silica. Therefore, the electronic and optical properties of defect-free and hydrogen defects in amorphous silica were performed within the scheme of density functional theory. Initially, the negative charged states hydrogen defects introduced new defect level between the valence band top and conduction band bottom. However, the neutral and positive charged state hydrogen defects made both the valence band and conduction band transfer to the lower energy. Subsequently, the optical properties such as absorption spectra, conductivity and loss functions were analyzed. It is indicated that the negative hydrogen defects caused the absorption peak ranging from 0 to 2.0 eV while the positive states produced absorption peaks at lower energy and two strong absorption peaks arose at 6.9 and 9.0 eV. However, the neutral hydrogen defects just improved the intensity of absorption spectrum. This may give insights into understanding the mechanism of laser-induced damage for optical materials. -
References
[1] Skuja L, Kajihara K, Hirano M, et al. Visible to vacuum-UV range optical absorption of oxygen dangling bonds in amorphous SiO2. Phys Rev B, 2011, 84: 205206 doi: 10.1103/PhysRevB.84.205206[2] Pacchioni G, Skuja L, Griscom D L. Defects in SiO2 and related dielectrics, science and technology. Springer, 2000[3] Skuja L, Hirano M, Hosono H, et al. Defects in oxide glasses. Phys Status Solid C, 2005, 2(1): 15 doi: 10.1002/(ISSN)1610-1642[4] Benoit M, Pöhlmann M, Kob W. On the nature of native defects in high OH-content silica glasses: a first-principles study. Europhys Lett, 2008, 82(5): 57004 doi: 10.1209/0295-5075/82/57004[5] Kajihara K, Hirano M, Skuja L, et al. Vacuum-ultraviolet absorption of hydrogenated and deuterated silanol groups and interstitial water molecules in amorphous SiO2. Phys Rev B, 2005, 72: 214112 doi: 10.1103/PhysRevB.72.214112[6] Van Ginhoven R M, Hjalmarson H P, Edwards A H, et al. Hydrogen release in SiO2: source sites and release mechanisms. Nucl Instrum Meth B, 2006, 250: 274 doi: 10.1016/j.nimb.2006.04.123[7] Godet J and Pasquarello A. Ab initio study of charged states of H in amorphous SiO2. Microelectron Eng, 2005, 80: 288 doi: 10.1016/j.mee.2005.04.082[8] Edwards A H, Shedd W M, Pugh R D. The theory of H- in SiO2. J Non-Cryst Solids, 2001, 289(1-3): 42 doi: 10.1016/S0022-3093(01)00649-4[9] Skuja L, Kajihara K, Hirano M, et al. Fluorine laser-induced silicon hydride Si–H groups in silica. J Non-Cryst Solids, 2007, 353(5–7): 526 doi: 10.1016/j.jnoncrysol.2006.10.020[10] Zachariasen W H. The atomic arrangement in glass. J Am Chem Soc, 1932, 54: 3841 doi: 10.1021/ja01349a006[11] Warren B E. The diffraction of X-rays in glass. Phys Rev, 1934, 45: 657 doi: 10.1103/PhysRev.45.657[12] Khein A, Ashcroft N W. Generalized density functional theory. Phys Rev Lett, 1997, 78: 3346 doi: 10.1103/PhysRevLett.78.3346[13] Perdew J P, Burke K, Ernerhof M. Generalized gradient approximation made simple. Phys Rev Lett, 1996, 77: 3865 doi: 10.1103/PhysRevLett.77.3865[14] Perdew J P, Chevary J A, Vosko S H, et al. Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys Rev B, 1992, 46: 6671 doi: 10.1103/PhysRevB.46.6671[15] Ren D H, An X Y, Cheng X L, et al. Phase transition and elastic properties of NbN under hydrostatic pressure. J Wuhan Univ Technol-Mater Sci Ed, 2014, 29: 49 doi: 10.1007/s11595-014-0866-y[16] Pack J D, Monkhorst H J. Special points for Brillouin-zone integrations—a reply. Phys Rev B, 1977, 16: 1748 doi: 10.1103/PhysRevB.16.1748[17] Mozzi R L, Warren B E. The stucture of vitreous silica. J Appl Crystallogr, 1969, 2: 164 doi: 10.1107/S0021889869006868[18] Li N, Ching W Y. Structural, electronic and optical properties of a large random network model of amorphous SiO2 glass. J Non-Cryst Solids, 2014, 383: 28 doi: 10.1016/j.jnoncrysol.2013.04.049[19] El-Sayed A M, Watkins M B, Shluger A L, et al. Identification of intrinsic electron trapping sites in bulk amorphous silica from ab initio calculations. Microelectron Eng, 2013, 109: 68 doi: 10.1016/j.mee.2013.03.027[20] Jin T, Li X, Sun H. Interaction mechanisms between poly(amido-amine) and nano-silicon dioxide. Int J Quantum Chem, 2013, 113(8): 1213 doi: 10.1002/qua.v113.8[21] Jin T, Kong F M. Effect of differently terminal groups of poly(amido-amine) dendrimers on dispersion stability of nano-silica and ab initio calculations. Surf Interface Anal, 2015, 47(4): 474 doi: 10.1002/sia.5735[22] Jin T, Zhang F. Interaction mechanism of ultrafine silica and poly(amido-amine) and dispersibility of the complexes in coatings. Prog Org Coat, 2013, 76(2/3): 447 doi: 10.1016/j.porgcoat.2012.10.011[23] Fox M. Optical properties of solids. New York: Oxford University Press, 2001[24] Wooten F. Optical properties of solids. New York: Acadmic Press, 1972[25] Tamura T, Ishibashi S, Tanaka S, et al. First-principles analysis of optical absorption edge in pure and fluorine-doped SiO2 glass. Comput Mater Sci, 2008, 44: 61 doi: 10.1016/j.commatsci.2008.01.065[26] Vella E, Messina F, Cannas M, et al. Unraveling exciton dynamics in amorphous silicon dioxide: interpretation of the optical features from 8 to 11 eV. Phys Rev B, 2011, 83: 174201 doi: 10.1103/PhysRevB.83.174201[27] Morimoto Y, Nozawa S, Hosono H. Effect of Xe2 light (7.2 eV) on the infrared and vacuum ultraviolet absorption properties of hydroxyl groups in silica glass. Phys Rev B, 1999, 59: 4066 doi: 10.1103/PhysRevB.59.4066 -
Proportional views
