| Citation: |
Zhidi Jiang, Zhenhai Wang, Pengjun Wang. Delay-area trade-off for MPRM circuits based on hybrid discrete particle swarm optimization[J]. Journal of Semiconductors, 2013, 34(6): 065007. doi: 10.1088/1674-4926/34/6/065007
****
Z D Jiang, Z H Wang, P J Wang. Delay-area trade-off for MPRM circuits based on hybrid discrete particle swarm optimization[J]. J. Semicond., 2013, 34(6): 065007. doi: 10.1088/1674-4926/34/6/065007.
|
Delay-area trade-off for MPRM circuits based on hybrid discrete particle swarm optimization
DOI: 10.1088/1674-4926/34/6/065007
More Information
-
Abstract
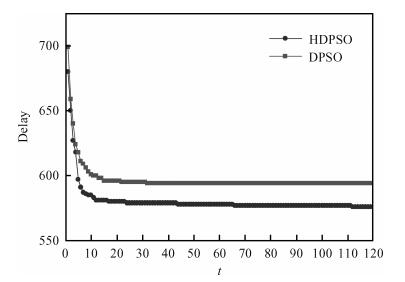
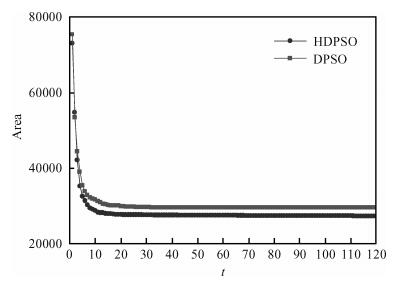
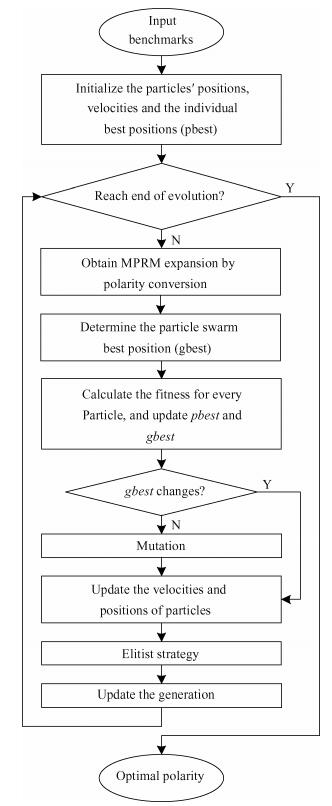
Polarity optimization for mixed polarity Reed-Muller (MPRM) circuits is a combinatorial issue. Based on the study on discrete particle swarm optimization (DPSO) and mixed polarity, the corresponding relation between particle and mixed polarity is established, and the delay-area trade-off of large-scale MPRM circuits is proposed. Firstly, mutation operation and elitist strategy in genetic algorithm are incorporated into DPSO to further develop a hybrid DPSO (HDPSO). Then the best polarity for delay and area trade-off is searched for large-scale MPRM circuits by combining the HDPSO and a delay estimation model. Finally, the proposed algorithm is testified by MCNC Benchmarks. Experimental results show that HDPSO achieves a better convergence than DPSO in terms of search capability for large-scale MPRM circuits. -
References
[1] Habib M K. A new approach to generate fixed-polarity Reed-Muller expansions for completely and incompletely specified functions. International Journal of Electronics, 2002, 89(11):845 doi: 10.1080/0020721031000093129[2] Younes A, Miller J F. Representation of Boolean quantum circuits as reed-Muller expansions. 2004, 91(7): 431[3] Al Jassani B A, Urquhart N, Almaini A E A. Manipulation and optimisation techniques for Boolean logic. IET Computers and Digital Techniques, 2010, 4(3):227 doi: 10.1049/iet-cdt.2009.0007[4] Zhang Huihong, Wang Pengjun, Gu Xingsheng. Area optimization of fixed-polarity Reed-Muller circuits based on niche genetic algorithm. Chinese Journal of Electronics, 2011, 20(1):27 doi: 10.1007%2FBF01271287.pdf[5] Liao C J, Tseng C T, Luarn P. A discrete version of particle swarm optimization for flowshop scheduling problems. Computers and Operations Research, 2007, 34(10):3099 doi: 10.1016/j.cor.2005.11.017[6] Sandesh S, Shankar K. Application of a hybrid of particle swarm and genetic algorithm for structural damage detection. Inverse Problems in Science and Engineering, 2010, 18(7):997 doi: 10.1080/17415977.2010.500381[7] Chen W N, Zhang J, Chung H S H, et al. A novel set-based particle swarm optimization method for discrete optimization problems. IEEE Trans Evolutionary Computation, 2010, 14(2):278 doi: 10.1109/TEVC.2009.2030331[8] Wang Pengjun, Li Hui. Low power mapping for AND/XOR circuits and its application in searching the best mixed-polarity. Journal of Semiconductors, 2011, 32(2):025007 doi: 10.1088/1674-4926/32/2/025007[9] Cortadella J. Timing-driven logic bi-decomposition. IEEE Trans Computer-Aided Design of Integrated Circuits and Systems, 2003, 22(6):675 doi: 10.1109/TCAD.2003.811447[10] Hrynkiewicz E, Koldzińki S. An Ashenhurst disjoint and non-disjoint decomposition of logic functions in Reed-Muller spectral domain. Proceedings of Mixed Design of Integrated Circuits and Systems, Wroclaw, 2010:200 https://projecteuclid.org/euclid.jam/1439816408[11] Pourjafari E, Mojallali H. Predictive control for voltage collapse avoidance using a modified discrete multi-valued PSO algorithm. ISA Transactions, 2011, 50(2):195 doi: 10.1016/j.isatra.2010.12.006[12] Kuo R J, Han Y S. A hybrid of genetic algorithm and particle swarm optimization for solving bi-level linear programming problem——a case study on supply chain model. Applied Mathematical Modelling, 2011, 35(8):3905 doi: 10.1016/j.apm.2011.02.008 -
Proportional views





 DownLoad:
DownLoad: