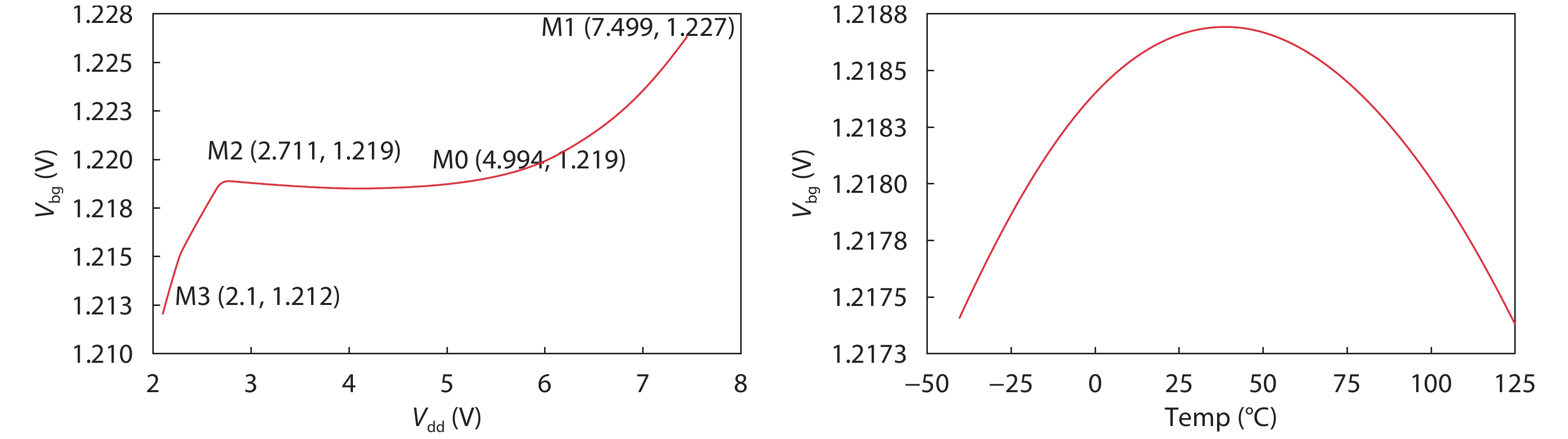1. Introduction
The idea of sigma–delta (Σ–Δ) modulation was first proposed in 1962 by Inoise et al.[1], who described a modulator structure with a continuous-time integrator as circular filter and a Schmitt latch as a quantizer and implemented a 40-dB SNR analog to digital converter (ADC). In 1974, Richie et al. advanced the idea of employing a high-order circular filter to achieve high-performance ADCs[2]. Subsequently, Candy et al. proposed a method of analyzing and designing Σ–Δ ADCs theoretically and also put forward the MASH (multi-stage noise shaping) structure[3-8]. The MASH structure was first employed by Hayashi et al. to realize Σ–Δ ADCs[8]. Because of the rapid development of the integrated circuit manufacture process technology, the concept of realizing a high system resolution in exchange for speed has been successfully applied, with 31-bit high-precision Σ–Δ ADCs currently being constructed. These high precision Σ–Δ ADCs usually employ high 4- or 5-order stages. Significant research on Σ–Δ ADCs has been undertaken in recent years and marked progress has been made; however, the implemented architectures are limited to 2- or 3-order stages with a precision below 16-bit[9-12].
Structurally, the Σ–Δ ADC is divided into two parts: a front-end analog modulator and a back-end digital filter. The performance of the front-end analog modulator has a decisive influence on the performance of the Σ–Δ ADC. Principally, a higher precision can be achieved with higher-order front-end analog modulators. However, higher-order modulators (e.g., 4- or 5-order modulators) face stability issues. At the same time, the input signal range decreases with higher-order structures. Currently, the most widely used structures are of 4-orders or less. Increasing the modulator’s orders while maintaining stability is an important field of research. Caldwell et al.[13] proposed an 8-order modulator in 2009 with an oversampling rate (OSR) of 3. The MASH structure cuts down the high-order single-loop to a low-order multi-loop to avoid stability issues; however, because of mismatch arising from the integrated circuit manufacturing process, designing Σ–Δ ADCs based on the MASH structure has been hard to accomplish. With continued advances in the manufacturing process and the persistence of high-order stability issues, the MASH structure has increasingly been used to implement high-precision Σ–Δ ADCs. Chiang et al.[14] implemented a 14-bit Σ–Δ ADC with the MASH structure using a 2.5-V power supply and Yao et al.[15] designed a 15-bit Σ–Δ ADC using a 130 nm process technology with a power supply of only 1.0-V and power dissipation of 7.4 mW. Chen et al. [9] proposed a promising Σ–Δ modulator for GSM systems and achieved an 80 dB dynamic range with a 1.8-V power supply and 16.7 mW power dissipation.
In this paper, a 4-order single-loop Σ–Δ switched-capacitor modulator with a CIFB (cascade-of-integrators feed-back) architecture is proposed for the design of a high-order single-loop modulator. This paper is structured as follows. In section 2, the 4-order single-loop CIFB Σ–Δ modulator architecture is proposed, and the noise transfer function (NTF) of the proposed structure is given and mapped to the CIFB parameters. Section 3 provides details on the implementation of the critical circuits. Section 4 presents the ASIC test results, and section 5 provides the conclusions for the paper.
2. Σ–Δ modulator architecture
The performance of the Σ–Δ modulator depends primarily on the NTF. For physical implementation considerations,
|
H(z)=NTF(z)=N(z)D(z)=m∑i=0aizi/n∑j=0ajzj. |
(1) |
Fig. 1 shows the noise modulation results with different modulation orders. The results show that as the modulation order increases, more low-frequency noise is modulated into the high-frequency domain. The realization of a high precision ADC can be anticipated after back-end low-pass digital filter filtering of the high-frequency noise.
According to Ref. [17], the signal quantization noise rate (SQNR) can be expressed as follows:
|
SQNR∝10log2N+1π2N+(20N+10)log(OSR), |
where N is the modulation stages.
To realize a high-precision Σ–Δ ADC, a higher N and OSR leads to improved performance; however, as mentioned earlier, the stability and input range of the structure decreases with increasing modulation stages. In this work, N was designed as 4 and the OSR was selected as 128. By employing the Look-up table method to obtain zeros and the Butterworth filter method to get the poles[17], the NTF could be optimized as follows:
|
H(z)=NTF(z)=z4−3.999z3+5.999z2−3.999z+1z4−3.181z3+3.86z2−2.112z+0.4383. |
(2) |
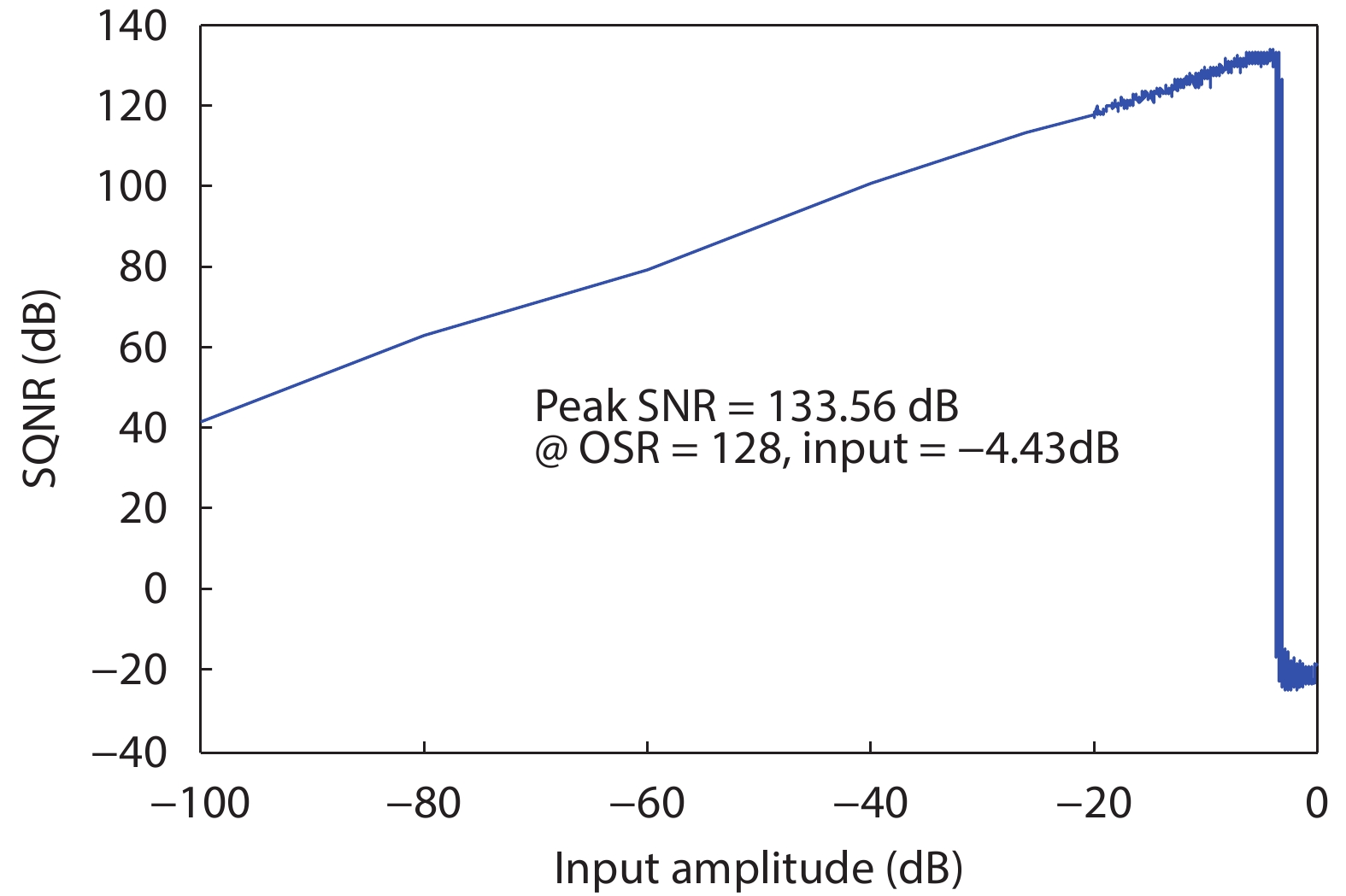
The simulated relationship between the SQNR and the input signal amplitude is displayed in Fig. 2.
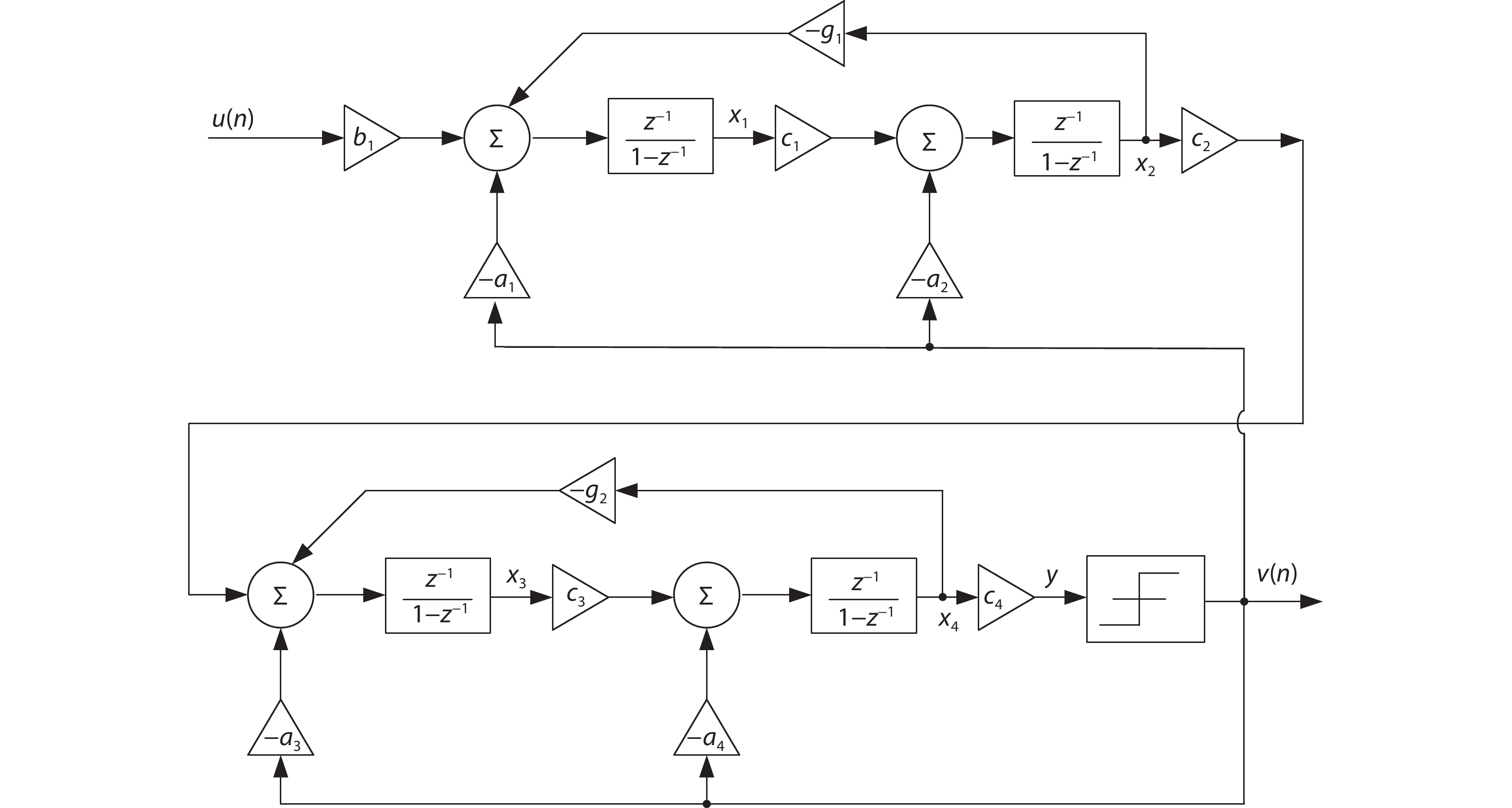
The CIFB modulator is a cascade of several integrators with feedbacks. Fig. 3 displays the 4-order single-loop CIFB modulator structure designed in this work. The signal transfer function (STF) is a low-pass filter under the CIFB structure, which can suppress out of band signals.
The NTF corresponding to the CIFB structure in Fig. 3 is as follows:
|
NTFk=1(z)=(z−1)4+(c1g1+c3g2)(z−1)2+c1c3g1g2(z−1)4+a4c4(z−1)3+(a3c3c4+c1g1+c3g2)(z−1)2+(a2c2c3c4+a4c1c4g1)(z−1)+(a1c1c2c3c4+a3c1c3c4g1+c1c3g1g2). |
According to the NTF formula (2), the mapped CIFB parameters could be obtained, as shown in Table 1[17].
| i | ai | gi | bi | ci |
| 1 | 0.00664 | 0.00007 | 0.0053 | 1 |
| 2 | 0.068261 | 0.00043 | – | 1 |
| 3 | 0.3165 | – | – | 1 |
| 4 | 0.819 | – | – | 1 |
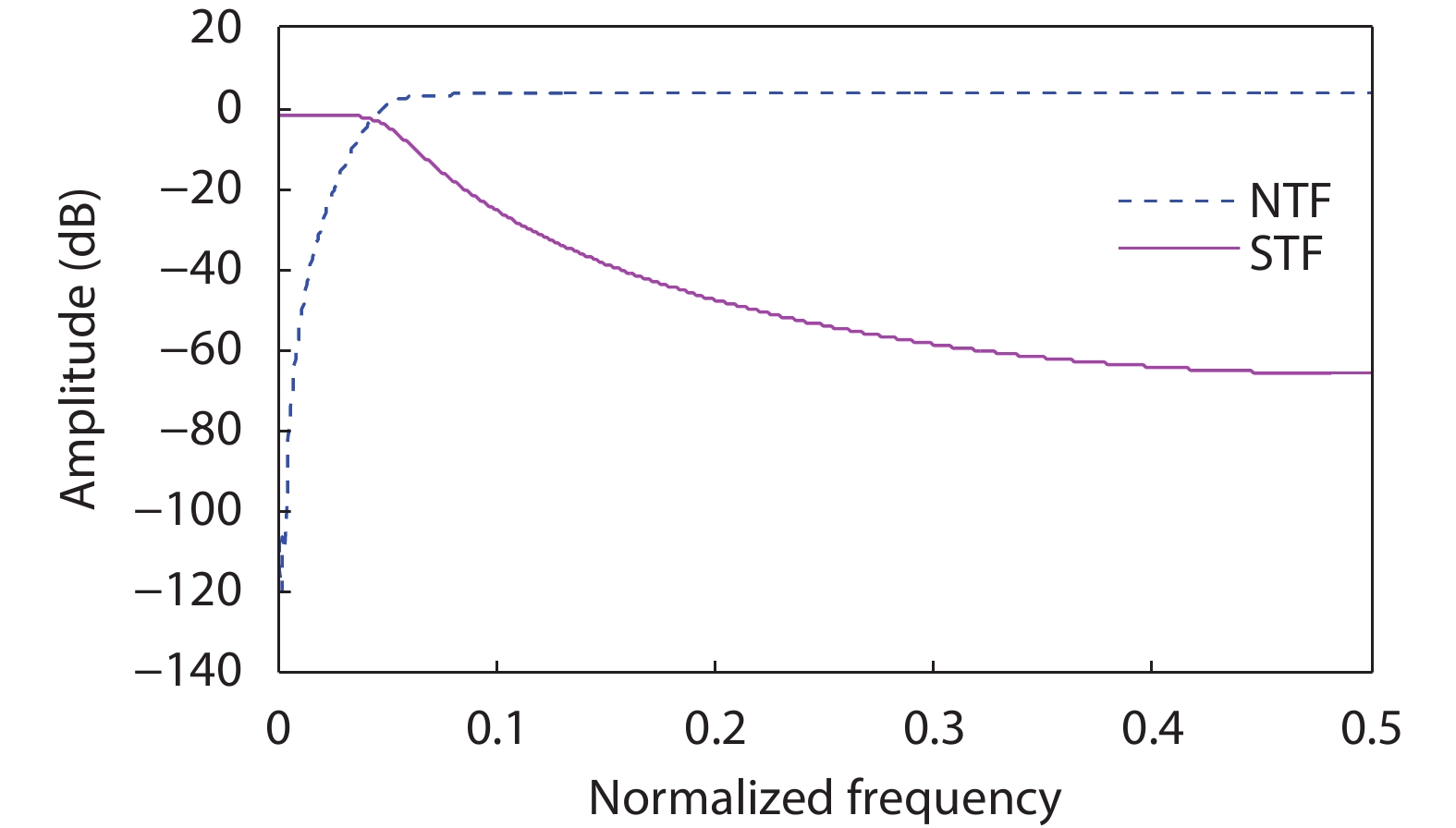
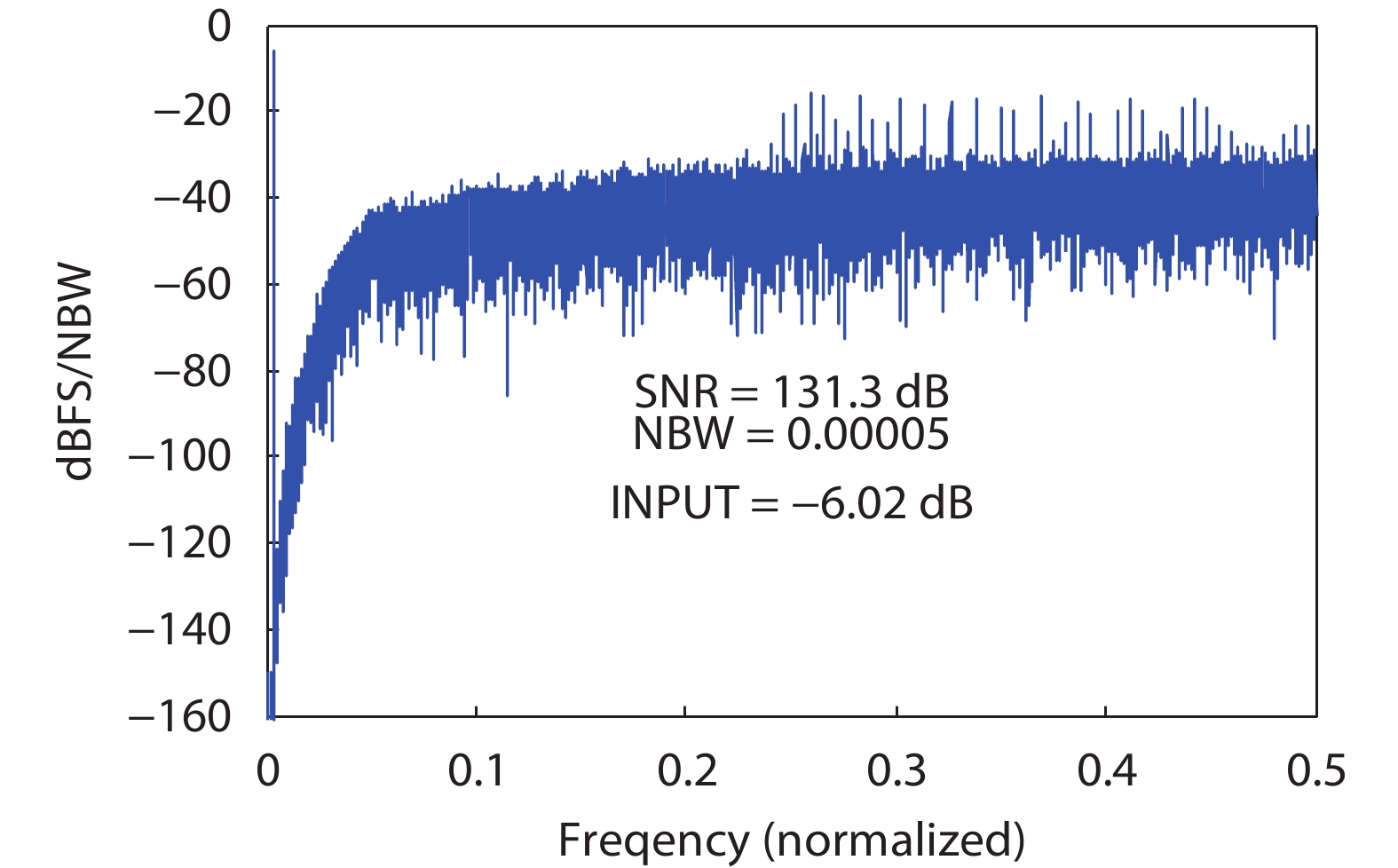
Fig. 4 depicts the designed NTF/STF transfer function, and Fig. 5 gives the simulated SQNR result under –6 dB input signal.
3. Circuit implementation
As Fig. 3 shows, the Σ–Δ modulator is essentially an IIR filter, which is cascaded with 4-stage integrators. Based on the work mode of the integrators, the Σ–Δ modulator can be divided into two classes: (1) continuous-time (CT) modulator and (2) switched-capacitor (SC) modulator. A CT modulator exhibits a higher bandwidth, low power dissipation, and contains an anti-aliasing circuit internally, so it is popular in wireless communication; however, CT modulation is more sensitive to clock jitter, feedback network delay, and resistor/capacitor mismatches arising from the manufacturing process, so achieving high precision is difficult. In contrast, the SC modulator is bandwidth limited (generally less than 1 MHz) but less sensitive to parameter fluctuation; hence, it is adopted widely for high precision Σ–Δ modulator designs. In this work, the SC modulator was employed to implement the CIFB structure, which is shown in Fig. 6.
According to Fig. 6, the following critical circuits need to be implemented: the bandgap reference circuit, the operation amplifier (OTA), the clock generator, the comparator (1-bit quantizer), and latch.
3.1 Bandgap reference
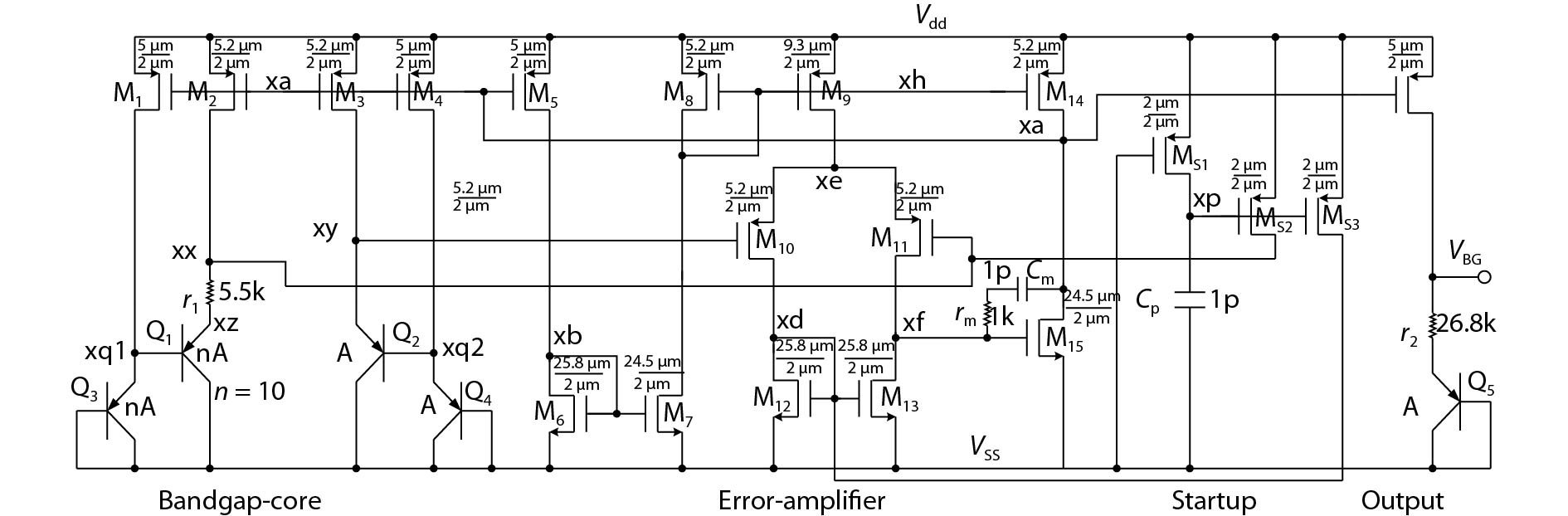
Essentially, the bandgap reference is a voltage reference generator circuit that employs two opposing temperature modulation mechanisms. The bandgap reference is ideally a zero-temperature drift voltage reference; however, because the positive or negative drift factors themselves depend on the temperature, it is hard to achieve absolute zero temperature drift voltage reference because of the presence of variances caused by the manufacturing process. Generally, over a wide temperature range, such as between –40 to 85 °C, 50-ppm/°C can be achieved. Fig. 7 shows the bandgap reference circuit designed in this work and Fig. 8 gives the simulated results.
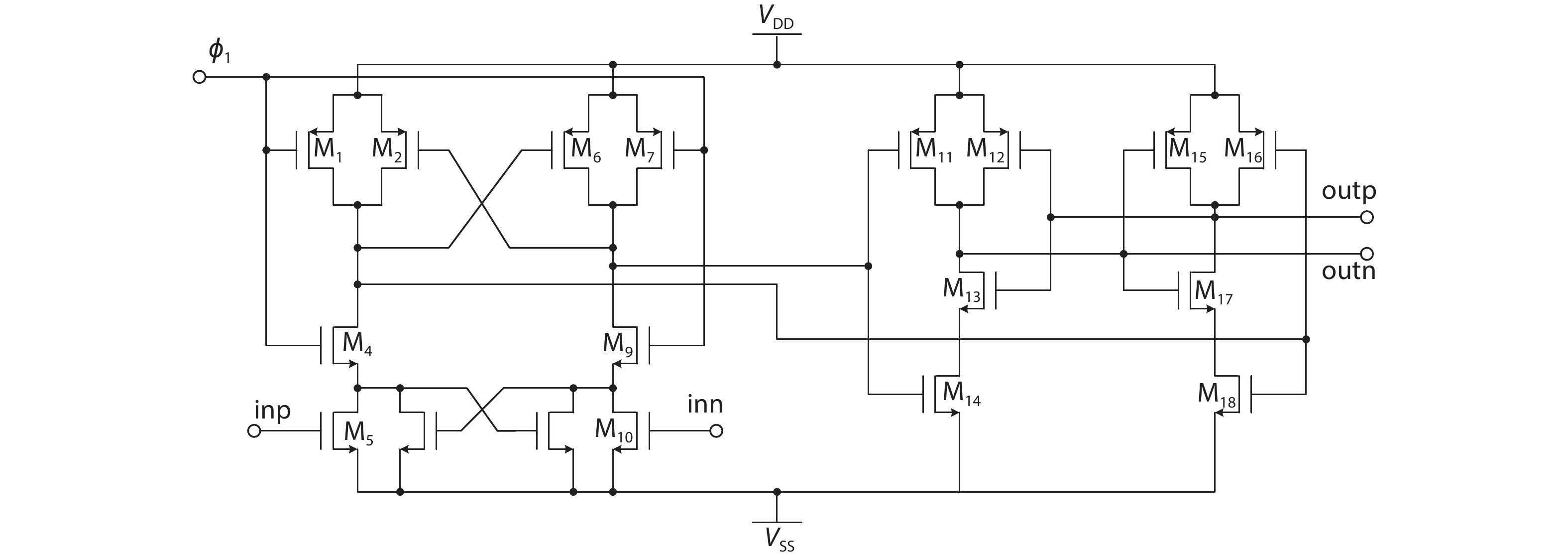
3.2 OTA
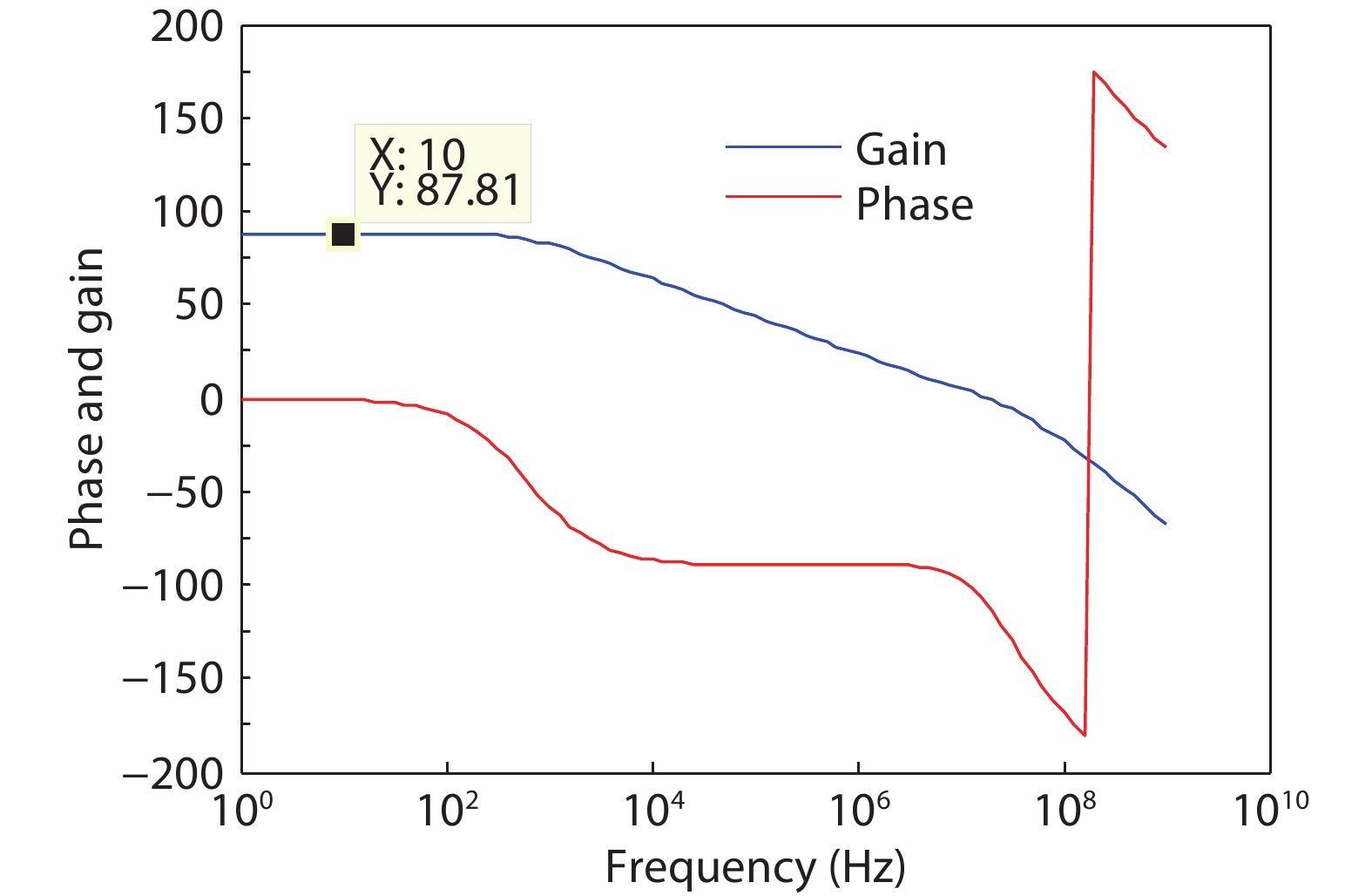
In this work, a two-stage structure was adopted for the OTA, with the first stage providing high gain and the second stage providing a large swing. Wang et al.[18] conducted a detailed analysis and summarized the OTA types used in oversampling ADCs. Fig. 9 shows the OTA circuit used in this work and Fig. 10 gives the simulation results. Because a 4-order structure was adopted in this work for the modulator design, the gain requirements for the OTA were low. According to the simulation results, the achieved DC gain was 87.8 dB with a phase margin of 66º, and the results are summarized in Table 2.
| DC gain | Phase margin | Power dissipation | GBW | Common offset | Single-side swing | Slew rate | Effective input noise |
| 87.8 dB | 66° | 2.44 mW | 28 MHz | 100 nV | ±2.2 V | 5 V/μs | 14 nV/Hz1/2 (1 kHz) |
4. Clock generator
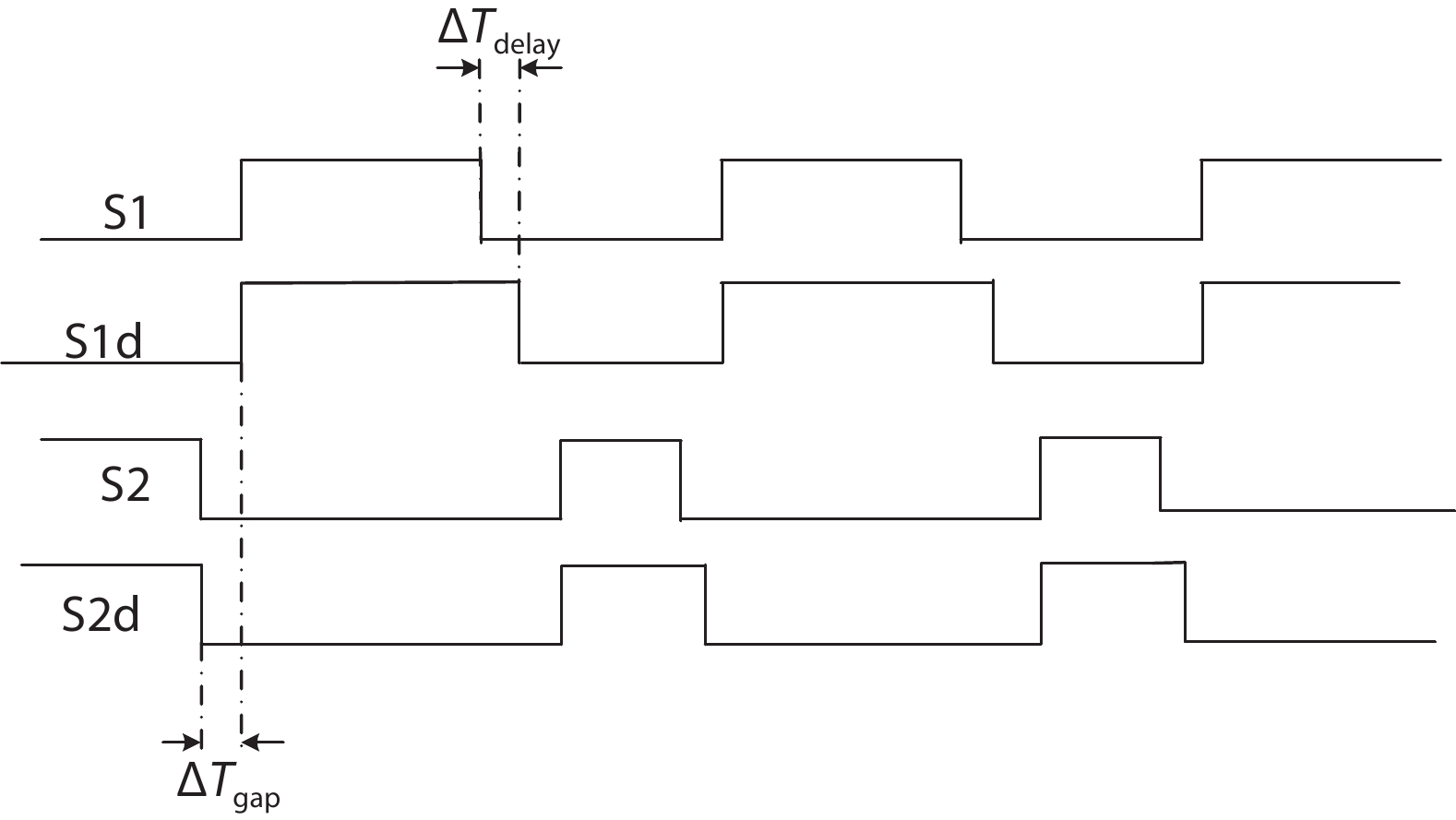
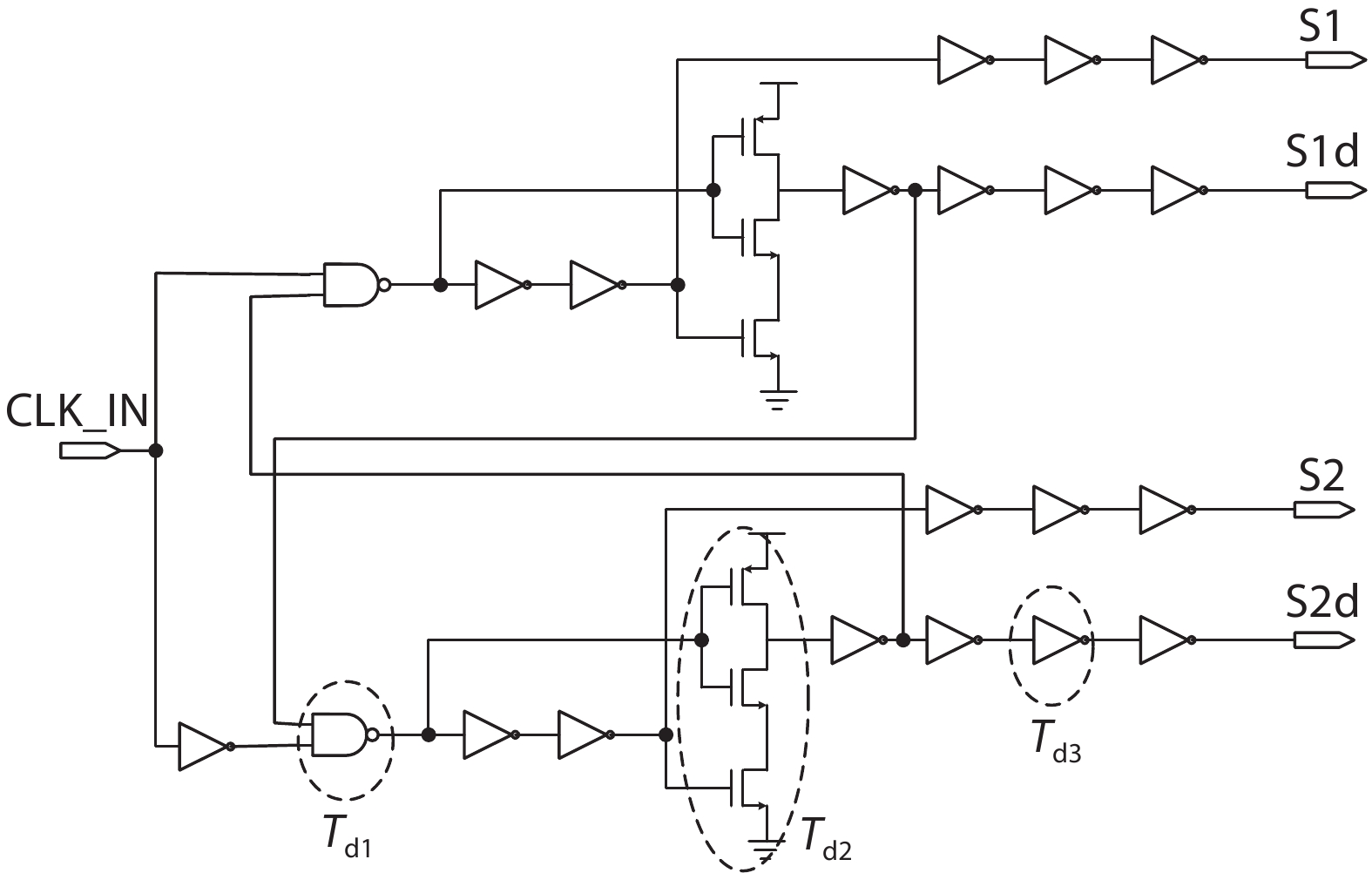
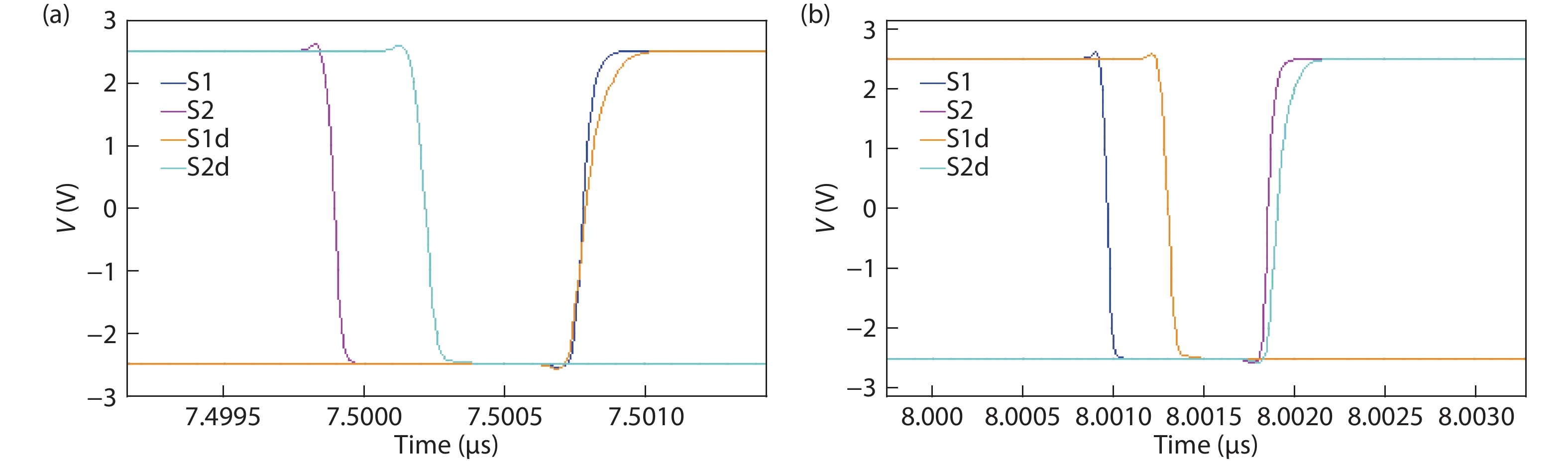
The SC modulator was a clock driven structure. As shown in Fig. 6, four clocks were needed S1, S1d, S2, and S2d, and the relationship of these clocks is displayed in Fig. 11.
The clock generator circuit was implemented as shown in Fig. 12. With the delay designated in the figure, the following relationship is obtained:
|
ΔTdelay(S1,S1d)=Td2+nTd3,n=1,ΔTgap(S1,S2)=Td1+Td2+mTd3,m=3. |
According to the simulation results in Fig. 13, switches with the same phase (S1/S1d or S2/S2d) turn on at the same time, while they turn off with a delay. An SC modulator requires that charge injection is avoided when the switches turn off.
5. Comparator and latch
The comparator is used as a 1-bit quantizer in the SC modulator. The comparator and latch are both digital circuits that have standard implementations. In this work, hysteresis was incorporated to avoid multiple-trigger issues because of close thresholds. The hysteresis essentially acts as a positive feedback system, and the comparator adopting this system is called a Schmitt comparator. The comparator and latch circuit implemented in this work are shown in Fig. 14.
6. Results
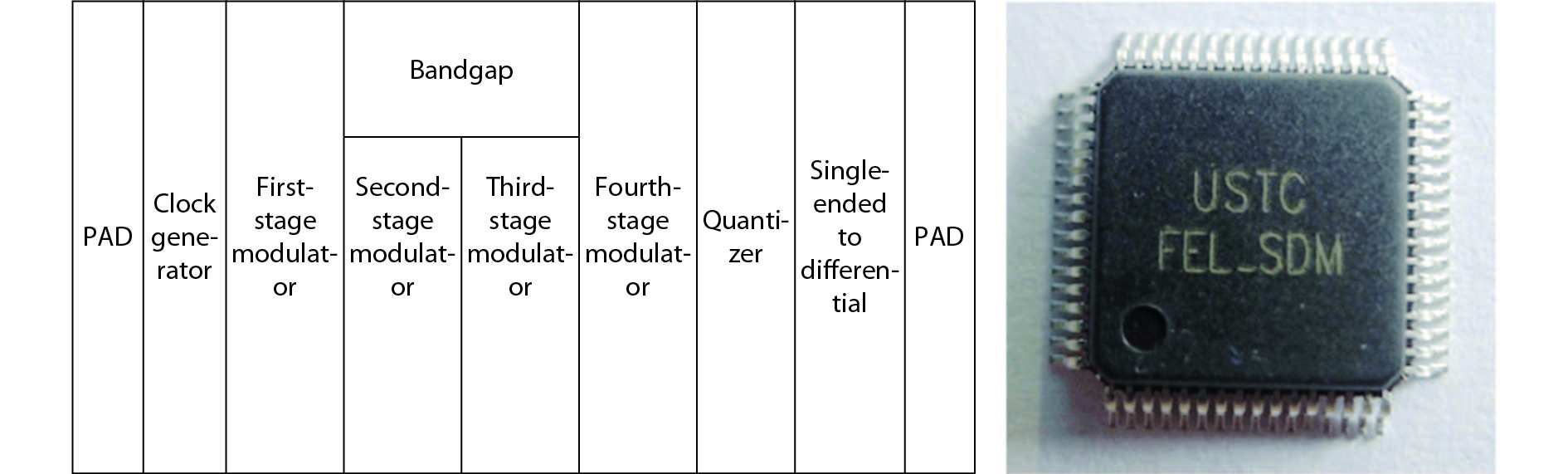
Based on the 4-order single-loop CIFB SC modulator structure with the circuits introduced in the previous section, a Σ–Δ modulator was implemented with a Chartered 0.35 μm CMOS process and a chip area of 1.72 × 0.75 mm2. The chip was operated with a 3.3-V power supply with a power dissipation of 22 mW. Fig. 15 shows the chip layout and Fig. 16 shows the layout architecture and the manufactured chip.
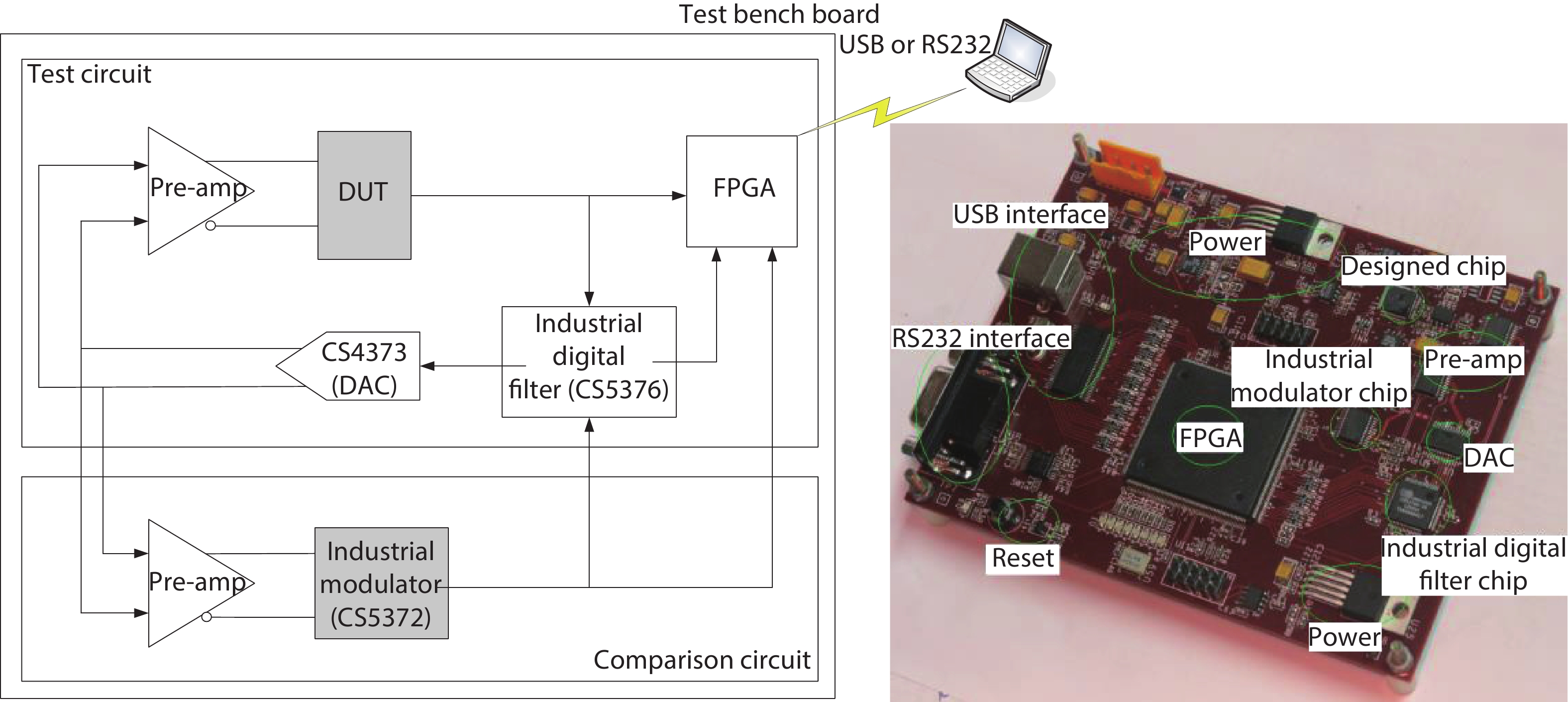
To thoroughly evaluate the chip performance, a test bench was designed for the chip and a mature industrial chip was used for comparison. The test bench architecture and the test board are displayed in Fig. 17.
The test bench included the following components: signal source: CS4373, output high-precision sinusoidal wave with SNR > 114 dB; digital filter: CS5376 with comb filter, FIR filter, IIR filter internally; modulator for comparison: CS5372, high-precision Σ–Δ modulator used widely in the seismic exploration field.
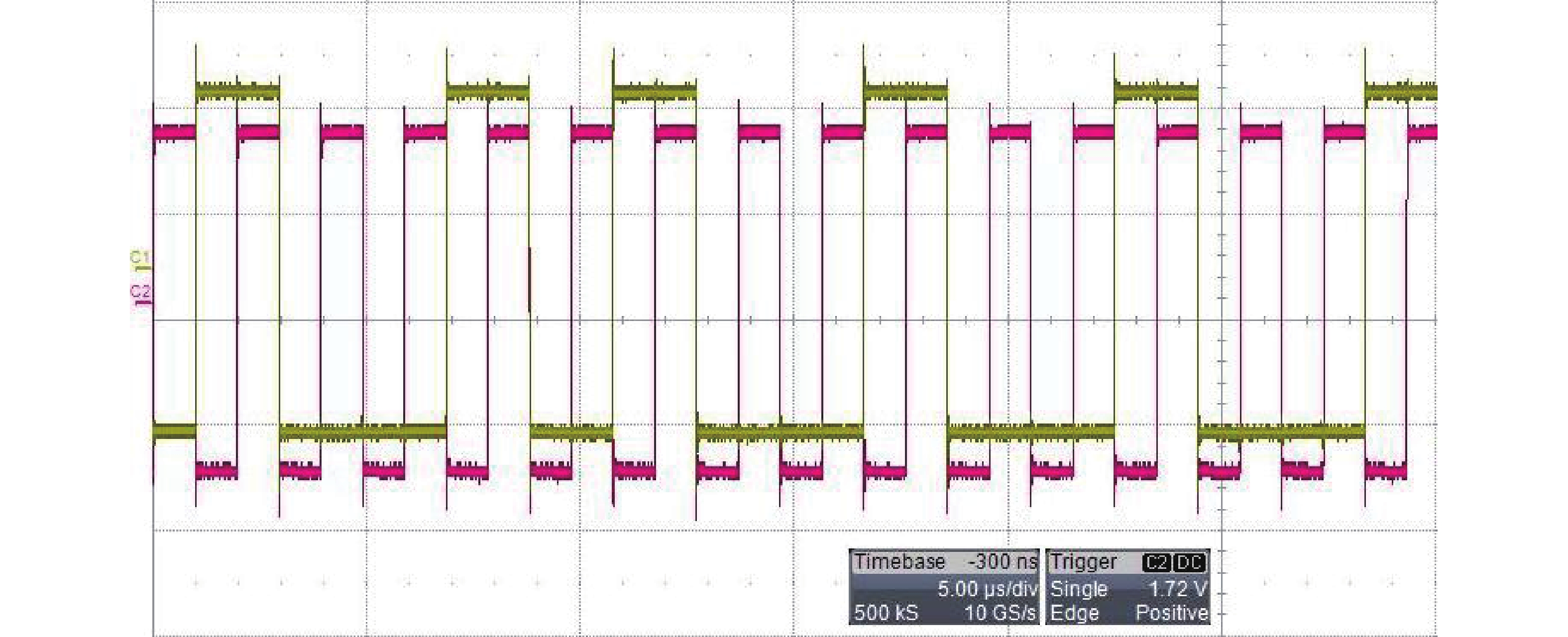
Fig. 18 shows the modulated bit stream (time domain waveform) output of the designed Σ–Δ modulator. The bit stream outputs at the falling edge of the output clock. The bit rate was 512 kbps, which is the same as CS5372.
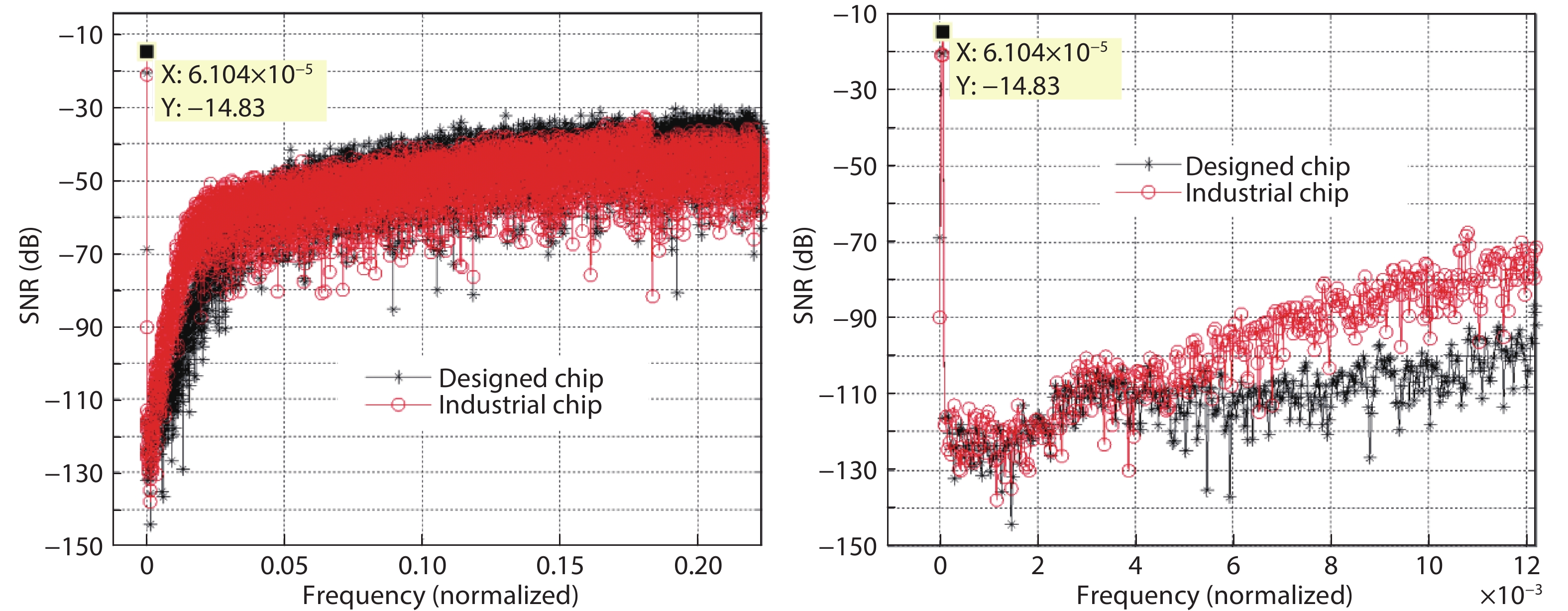
Fig. 19 shows a comparison of the raw modulated bit stream performance and Fig. 20 shows a performance comparison after digital filtering for both the designed and industrial (CS5372) chips. The designed chip shows improved performance compared with the mature industrial chip for some parameters. Table 3 summarizes the comparison results.
| Performance | This work | CS5372 |
| SNR (dB) | 93.79 | 93.09 |
| THD (dB) | –101.64 | –102.22 |
| SINAD (dB) | 93.13 dB | 92.59 |
| ENOB (bit) | 15.18 | 15.09 |
| SFDR (dB) | 105.82 | 105.09 |
| ENOB@FS (bit) | 17.65 | 17.56 |
FOM-w (figure of merit-w) is a general evaluation index[19] for performance comparison between different Σ–Δ modulators that may use different process technologies, power supplies, or bit stream rates. Under this evaluation index, the performance of the Σ–Δ modulators is mainly decided by the power dissipation, ENOB, and digital output rate (DOR):
|
FOM−w=Power(W)2resolution(bit)×DOR(samples)×1012. |
In addition to FOM-w, the FOM-v evaluation index[20] was considered; it takes into account the power supply, resolution, and DOR. Both FOM-w and FOM-v are good criteria for evaluating the performance of different Σ–Δ modulators. Generally speaking, a lower FOM index indicates a better Σ–Δ modulator performance. Table 4 compares the performance of several high-order Σ–Δ modulators that have been reported in recent years.
| Parameter | ENOB | DOR | Dissipation (mW) | CMOS process (µm) | Power supply (V) | Orders | OSR | Quantizer (bit) | FOM-w |
| Geets[21] | 11.5 | 12.5 Msps | 152 | 0.65 | 5 | 3 | 8 | 1 | 4.20 |
| Balmelli[22] | 13.6 | 2.5 Msps | 200 | 0.18 | 1.8 | 5 | 8 | 4 | 6.44 |
| Brigati[23] | 16.9 | 400 sps | 50 | 0.6 | 5 | 4 | 320 | 1 | 1022.1 |
| Gerosa[24] | 9.1 | 256 sps | 0.0018 | 0.8 | 1.8 | 3 | 16 | 8 | 12.8 |
| Yao[25] | 14.3 | 500 ksps | 7.4 | 0.13 | 1.0 | 4 | 64 | 1 | 0.73 |
| Chen[26] | 12.0 | 48 ksps | 30 | 0.5 | 5 | 5 | 64 | 1 | 8.30 |
| This work | 17.6 | 512 ksps | 22 | 0.35 | 3.3 | 4 | 128 | 1 | 1.63 |
According to the analysis in Section 2, the higher OSR and orders, the higher SNR, thus the higher ENOB would be achieved. The internal driver frequency is generally decided by the DOR: the higher the DOR, the higher the driver frequency, thus the higher the power dissipation. Another critical point is the power supply: the higher the power supply, the higher the power dissipation. Quantizer and process manufacture process play relatively less important roles than the previous factors. Special attention should be paid to the work of Brigati et al.[23], its FOM-w is very large. The reason is that its power dissipation is relatively large while with a very small DOR. This means that the achieved ENOB is good but with unacceptable power dissipation. The FOM-w for the modulator designed in this work is 1.63, which indicates good performance. In our design, the four stages all employ the same operational amplifier. According to our test, the first-stage plays a much more important role than others in the modulator’s performance. Thus, we could use a relatively simple amplifier structure in other three stages, which could further decrease the power dissipation in future.
7. Conclusion
In this paper, a 4-order single-loop SC modulator with a CIFB structure was proposed. Based on the proposed structure, the implementation of the critical circuits was illustrated and verified via simulations. The modulator chip was successfully manufactured using the Chartered 0.35 μm CMOS process, with a chip area of 1.72 × 0.75 mm2. The chip operated under a 3.3-V power supply with a power dissipation of 22 mW. The test results showed the designed modulator chip had improved performance compared with a mature industrial chip, and its ENOB was almost 18-bit. Therefore, it could be used in audio, digital TV, wireless communication and oil exploration, where demand high requirements for low frequency noise or high precision.
Acknowledgment
This paper has been funded by the Major Emerging Industrial Projects of Anhui, and the Postdoctoral Project from Hefei. The authors gratefully acknowledge the financial support and wish to express their thanks to the referees for critically reviewing the manuscript and making important suggestions.





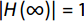
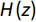

 DownLoad:
DownLoad:
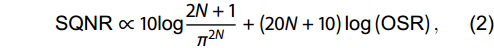
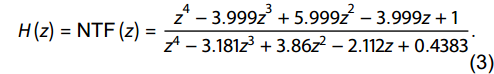


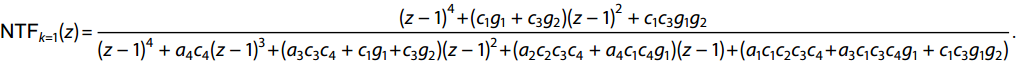









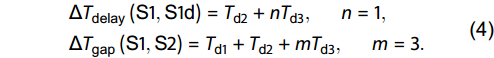








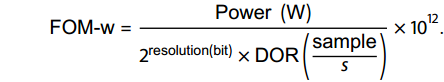

 DownLoad:
DownLoad: