1. Introduction

Suffering from low carrier mobility and electrical instability^{[1, 2]},thin-film transistors (TFTs) with a dual-gate structure rather than a single-gate structure were recently suggested as the subject of future work^{[3, 4, 5, 6]}. Reports of the advantages of these devices concentrated on the enhancement of carrier mobility and the steeper sub-threshold slope. Meanwhile,the dual-gate structure may be used for shielding parasitic effects in typical vertically integrated electronics,making it particularly attractive for active matrix display and imaging applications^[3,7]. Before they emerge at large-scale circuit level,accurate and physical-based models with efficient computational time are highly desirable for circuit simulation tools.

The surface potential-based models of TFTs have attracted considerable attention in recent years^{[8, 9]}. One of the noteworthy features of these models is their ability to give an accurate and continuous description of drain current in a single-piece formula. Extensive research has already been devoted to the compact modeling of undoped double-gate MOSFETs (DG MOSFETs)^{[10, 11]}. However,compared with the former,one of main difficulties for modeling DG TFTs rests on the complicated distribution of density of states (DOS) in amorphous silicon (a-Si:H). More recent experimental methods reveal that the deep-level state near the mid-gap exhibits a peak structure distinctly within the a-Si:H^{[12, 13]}. In that context,the double exponential distribution of DOS,which is widely used in the modeling of a-Si:H TFTs^{[14, 15]},makes the model semi-empirical. 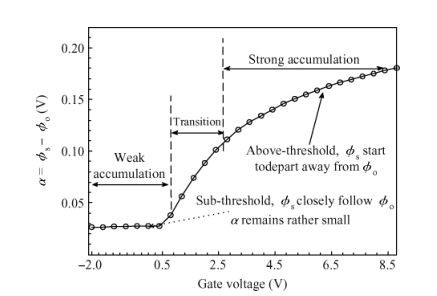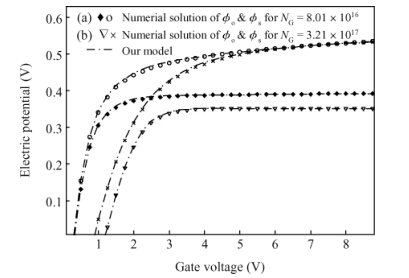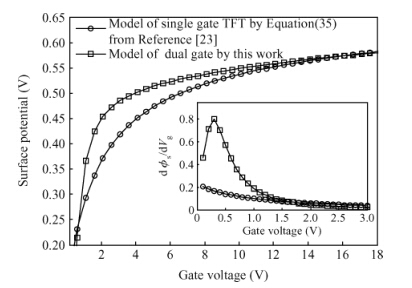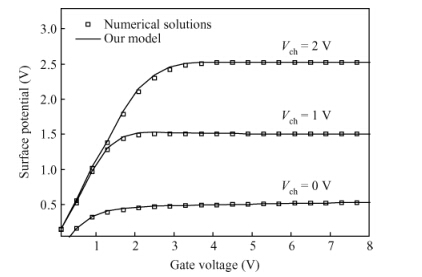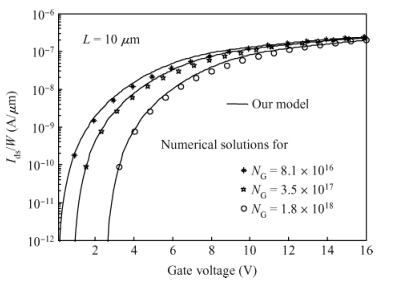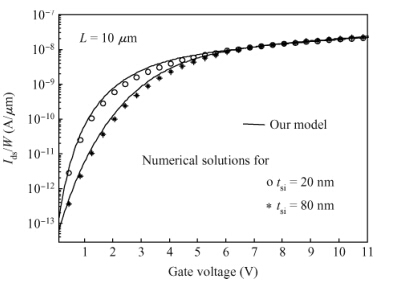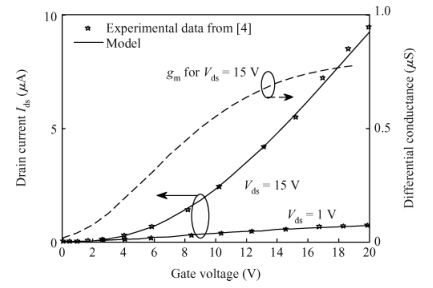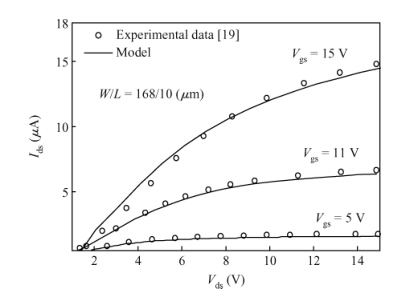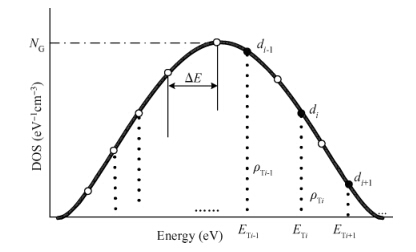It is now widely accepted that a more real and completed distribution of DOS in a-Si:H should be incorporated by taking both the deep Gaussian and tail exponential state of distribution into account. Apart from the complex distribution of DOS,another obstacle in the modeling of dual-gate a-Si:H TFTs is that the surface potential and potential near the middle of the layer are interrelated and cannot be treated independently. Servatiet al.^[3],Moonet al.^[4] and Takechi et al.^[5] have carefully investigated the current-voltage ($I$-$V$) characteristics and the top-gate effects of such devices; nevertheless,few studies have been carried out to assess the detail calculation of those inter-related potentials as well as the corresponding current model. It is therefore treated as the main concern of this paper.

Partly based on previous work^{[16, 17]},in what follows,we present a regional asymptotical scheme for modeling the potentials accounting for the combination of the different kinds of DOS in a-Si:H film. We show the parameters required for accurately describing the $I$-$V$ characteristics of these devices and how sensitively these parameters affect TFT current. The resulting scheme and current model have been compared with rigorous numerical simulations as well as the experimental data. A reasonable agreement has been achieved. The model may serve as an original point to develop a more advanced model for other such DG TFTs.

2. Approximation of potentials and drain current model

We consider a typical DG n-type intrinsic a-Si:H TFT working under the dual-gate biased mode. The generalized schematic structure of DG a-Si:H TFT has been given in References ^{[4, 17, 18]}. For simplicity's sake,in what follows,we treated the density of trap states throughout the a-Si:H film in a homogeneous way and assumed the field distribution in the active layer to be approximately symmetrical. The basic assumptions stated previously serve as a good approximation for the compact modeling of DG a-Si:H TFT and are a tradeoff between complexity and computation efficiency^[8,15,19].

The energy distribution of localized trap states (only acceptor-like is taken into account) can be roughly divided into two groups,which can be expressed as the following in detail:

$$\begin{align} \[{{N}_{\text{GA}}}(E)={{N}_{\text{G}}}\exp \left[ -{{\left( \frac{{{E}_{\text{GA}}}-E}{{{W}_{\text{GA}}}} \right)}^{2}} \right],\] \end{align}$$

(1)

$$\begin{align} \[{{N}_{\text{TA}}}(E)={{g}_{\text{t}}}\exp \frac{E-{{E}_{\text{C}}}}{k{{T}_{\text{t}}}},\] \end{align}$$

(2)

where $E$ is the trap energy,E_C is the conduction band edge,$N$_G is the peak density of deep states,$W$_GA is characteristic decay energy,$E_{\rm GA locates at which $N$_GA}(E) has the maximum value near the mid-gap,g_t and $T$_t are the acceptor-like density of tail states at the conduction band and the characteristic temperatures of the tail states,respectively. The total distribution of trap states is therefore given as $N(E)=N_{\rm GA}(E)+N_{\rm TA}(E)$.

$$\begin{align} \[{{n}_{\text{gaus}}}=\int_{{{E}_{\text{v}}}}^{{{E}_{\text{c}}}}{\frac{{{N}_{\text{GA}}}(E)}{1+\exp \frac{E-{{E}_{\text{FO}}}-q\phi }{kT}}}\text{d}E,\] \end{align}$$

(3)

where $E$_FO is the bulk Fermi level and $T$ is the room temperature. The integrated form of Equation (3) brings an obstacle when solving Poisson's equation. In this work,we treat this integration form approximately by discretizing the Gaussian distribution with a series of points $N$_i separated by ΔE from each other. Figure1 presents the discretion of DOS in details. Therefore,Equation (3) may be transformed to the following simple form:

$$\begin{align} \[{{n}_{\text{gaus}}}=\sum\limits_{i=1}^{N}{\frac{{{N}_{\text{i}}}}{1+{{K}_{\text{i}}}\exp \left( -\frac{q\phi }{kT} \right)}},\] \end{align}$$

(4)

where $

$${{N}_{\text{i}}}=\Delta E{{N}_{\text{G}}}\exp \left[ -{{\left( \frac{{{E}_{\text{i}}}-{{E}_{\text{GA}}}}{{{W}_{\text{GA}}}} \right)}^{2}} \right]$$ $ and $ $${{K}_{\text{i}}}=\exp \frac{{{E}_{\text{i}}}-{{E}_{\text{FO}}}}{kT}$$ $. Comparing Equations (3) and (4) numerically,one obtains a relative error of less than 1% when the interval of the Gaussian distribution is set larger than 10. We assume $N=10$ in the following work for simplicity. Note that the finite Sigma term given in Equation (4) instead of the integral in Equation (3) makes the following qualitative study more straightforward. Moreover,the discrete accumulative form of Equation (4) makes it more suitable for circuit simulation tools.

Following the SPICE model given in Reference ^[14],the density of free and tail trap charges in a-Si:H are written as

$$\begin{align} \[{{n}_{\text{free}}}={{N}_{\text{C}}}\exp \frac{q\phi -{{E}_{\text{FO}}}}{kT},\] \end{align}$$

(5)

$$\begin{align} \[{{n}_{\text{tail}}}={{g}_{\text{t}}}{{\phi }_{\text{Tail}}}\eta ({{T}_{\text{t}}})\exp \left[ \xi ({{T}_{\text{t}}})\frac{q\phi -{{E}_{\text{FO}}}}{kT} \right],\] \end{align}$$

(6)

where $

$$\begin{align} & \eta ({{T}_{\text{t}}})=\frac{2\pi -4}{3}{{(T/{{T}_{\text{t}}})}^{2}}+(6-2\pi )(T/{{T}_{\text{t}}})+(\frac{4\pi }{3}-8), \\ & \xi ({{T}_{\text{t}}})=-\frac{4}{15}{{(T/{{T}_{\text{t}}})}^{2}}+(T/{{T}_{\text{t}}})+\frac{1}{15},{{\phi }_{\text{Tail}}}=k{{T}_{\text{t}}}/q \\ \end{align}$$ $,and $N$_c is the effective density of states at the conduction band.

Neglecting the effect of hole concentration,the 1-D Poisson's equation along the $x$-direction can be expressed as

$$\begin{align} \[\frac{{{\partial }^{2}}\phi }{\partial {{x}^{2}}}=-\frac{\text{d}F}{\text{d}x}=\frac{q}{{{\varepsilon }_{\text{si}}}}({{n}_{\text{gaus}}}+{{n}_{\text{tail}}}+{{n}_{\text{free}}}),\] \end{align}$$

(7)

where $q$ is the electron charge and ${{\varepsilon }_{si}}$ is the silicon permittivity. Deploying Gauss's law for the symmetric DG (sDG) a-Si:H TFT results in the boundary condition given as

$$\begin{align} \[{{\left. \frac{\text{d}\phi }{\text{d}x} \right|}_{x=\frac{{{t}_{\text{si}}}}{2}}}=\frac{{{C}_{\text{ox}}}}{{{\varepsilon }_{\text{si}}}}({{V}_{\text{GS}}}-{{V}_{\text{FB}}}-{{\phi }_{\text{s}}}),\] \end{align}$$

(8)

$$\begin{align} \[{{\left. \frac{\text{d}\phi }{\text{d}x} \right|}_{x=0}}=0,\] \end{align}$$

(9)

where $

$${{t}_{si}}$$ $ is the a-Si:H film thickness,V_GS is the gate voltage,V_FB is the flat band voltage accounting for the effect of the work function of gate metal as well as the interface properties as given in References ^{[18, 20]},and C_ox is the effective nitride insulator capacitance per unit-area.

By using the relation $2(\partial \phi /\partial x)(\partial ^2\phi /\partial x^2)=(\partial /\partial x)(\partial \phi /\partial x)^2$ and integrating Equation (7) from the surface to the center of the film,the electric field at the surface of the layer is written as

$$\begin{align} \[\begin{align} & F(\phi ,{{V}_{\text{ch}}})=\sqrt{\frac{2q}{{{\varepsilon }_{\text{si}}}}}\left\{ \sum\limits_{i=1}^{N}{{{N}_{i}}}\left[ ({{\phi }_{\text{s}}}-{{\phi }_{\text{o}}})+{{G}_{\text{oi}}} \right]+{{N}_{\text{Tail}}} \right.\times \left[ 1-\exp \frac{-\xi ({{T}_{\text{t}}})({{\phi }_{\text{s}}}-{{\phi }_{\text{o}}})}{{{\phi }_{\text{t}}}} \right] \\ & \exp \frac{\xi ({{T}_{\text{t}}}){{\phi }_{\text{s}}}}{{{\phi }_{\text{t}}}}{{\left. +{{N}_{\text{FO}}}\left[ 1-\exp \frac{-({{\phi }_{\text{s}}}-{{\phi }_{\text{o}}})}{{{\phi }_{\text{t}}}} \right]\exp \frac{{{\phi }_{\text{s}}}}{{{\phi }_{\text{t}}}} \right\}}^{\frac{1}{2}}}, \\ \end{align}$$ \] \end{align}

(10)

where $G_{\rm oi}=\phi_{\rm t} \ln {\frac{1+K_{\rm i}\exp (-\frac{\phi_{\rm s}}{\phi_{\rm t}})}{1+K_{\rm i}\exp (-\frac{\phi_{\rm o}}{\phi_{\rm t}})}} $,$N_{\rm Tail}=\frac{kT g_{\rm t} \phi_{\rm Tail} \eta (T_{\rm t})}{\xi (T_{\rm t})}\exp \left[{-\frac{\left( {qV_{\rm ch}+E_{\rm FO}} \right)}{kT}} \right]$,and $N_{\rm FO}=N_{\rm C} \exp \left[{\frac{-(qV_{\rm ch}+E_{\rm FO})}{kT}} \right]$,$

$${{\phi }_{t}}$$ $ is the thermal voltage,V_ch stands for the channel quasi-Fermi level which equals 0 at the source and V_ds at the drain,$ $${{\phi }_{s}}$$ $ is the surface potential and ${{\phi }_{o}}$ is the potential at the middle of the film.

Applying the Gauss theorem to the oxide/a-Si interface and using Equation (10),an expression in terms of the surface potential $

$${{\phi }_{s}}$$ $ as well as the centric potential $ $${{\phi }_{o}}$$ $ can be obtained,i.e.,

$$\begin{align} \[{{V}_{\text{GS}}}-{{V}_{\text{FB}}}-{{\phi }_{\text{s}}}=\frac{{{\varepsilon }_{\text{si}}}}{{{C}_{\text{OX}}}}\cdot F({{\phi }_{\text{s}}},{{\phi }_{\text{o}}},{{V}_{\text{ch}}}).\] \end{align}$$

(11)

Note that similar to the DG MOSFETs,the electric field at the surface depends not only on $

$${{\phi }_{\text{s}}}$$ $ but on the difference of potentials $ $$\alpha ={{\phi }_{\text{s}}}-{{\phi }_{o}}$$ $. Numerical solutions to Equations (1)-(10) for difference in potential as a function of gate voltage are shown in Figure2. The typical parameters under study are listed in Table1. As shown in Figure2,at the beginning,the difference in potentials $\alpha $ remains rather small since the distribution of potential stays closely flat within the a-Si:H. With sustained growth of the gate voltage,the surface potential $ $${{\phi }_{\text{s}}}$$ $ starts to deviate away from the centric potential $ $${{\phi }_{o}}$$ $ and become dominant in determining the static characteristic of those devices.

We deploy the following asymptotical scheme for the accurate values of both surface and centric potential. At the beginning,initial values of $

$${{\phi }_{\text{s}}}$$ $ and $ $${{\phi }_{o}}$$ $ are provided. As in the case of the sub-threshold regime,most of the induced charge is trapped in Gaussian deep states under low gate bias. By using boundary condition (8),one therefore obtains the simplified equation which holds within this region as

$$\begin{align} \[{{V}_{\text{GS}}}-{{V}_{\text{FB}}}-{{\phi }_{\text{s}}}=\frac{\sqrt{2q{{\varepsilon }_{\text{si}}}}}{{{C}_{\text{ox}}}}{{\left\{ \sum\limits_{i=1}^{N}{{{N}_{i}}}\left[ ({{\phi }_{\text{s}}}-{{\phi }_{\text{o}}})+{{G}_{\text{oi}}} \right] \right\}}^{\frac{1}{2}}}.\] \end{align}$$

(12)

Since the dominant term on the RHS of Equation (10) is the density of traps,by twice making an integration of Equation (7) from the surface to the center of the layer,the first-order approximation value of $

$${{\phi }_{s}}-{{\phi }_{o}}$$ $,which is denoted as $ $${{\alpha }_{sub}}$$ $,can be roughly estimated as

$$\begin{align} \[{{\alpha }_{\text{sub}}}={{\phi }_{\text{s}}}-{{\phi }_{\text{o}}}\approx \frac{qt_{\text{si}}^{2}}{8{{\varepsilon }_{\text{si}}}}\sum\limits_{i=1}^{N}{{{N}_{i}}}.\] \end{align}$$

(13)

Note that Equation (13) shares a similar form to the doped DG MOSFET devices in the sub-threshold^[21]. Thus,the difference in potential in this regime can be roughly evaluated by both the concentration of deep trapped charges $N_i$ and the layer thickness $

$${{t}_{si}}$$ $.

With the increase in gate voltage,the quasi-Fermi level moves into the tailed state,the second item on the RHS of the equation becomes dominant,and one obtains the difference in potentials in this region being expressed as

$$\begin{align} \[\begin{align} & {{\alpha }_{\text{abv}}}={{\phi }_{\text{s}}}-{{\phi }_{\text{o}}}=-\frac{kT}{q\xi ({{T}_{\text{t}}})}\times \ln \{\cos [\frac{\sqrt{{{g}_{\text{t}}}kT\cdot \xi ({{T}_{\text{t}}})\cdot \eta ({{T}_{\text{t}}})\cdot t_{\text{si}}^{2}}}{4{{\phi }_{\text{t}}}} \\ & \times \exp \frac{-\left( {{E}_{\text{FO}}}+q{{V}_{\text{ch}}}+\xi ({{T}_{\text{t}}})\cdot q{{\phi }_{\text{o}}} \right)}{2kT}]\}. \\ \end{align}$$ \] \end{align}

(14)

Since the angle of the cosine function in Equation (14) cannot exceed $\pi /2$,one therefore finally obtains the centric potential $

$${{\phi }_{o}}$$ $ saturated to its maximum value,which is given by

$$\begin{align} \[{{\phi }_{\text{o}\ \text{max}}}=\frac{{{\phi }_{\text{t}}}}{\xi ({{T}_{\text{t}}})}\times \ln \frac{2{{\pi }^{2}}{{\varepsilon }_{\text{si}}}T}{{{q}^{2}}\eta ({{T}_{\text{t}}})\xi ({{T}_{\text{t}}}){{g}_{\text{t}}}t_{\text{si}}^{2}{{T}_{\text{t}}}\exp [-(q{{V}_{\text{ch}}}+{{E}_{\text{FO}}})/\phi t]},\] \end{align}$$

(15)

where $\phi_{\rm t}=kT/q$.

With respect of the value of surface potentials $

$${{\phi }_{\text{s}}}$$ $,as already mentioned,the localized charge trapped in the tail state dominates Poisson's equation. Since surface potential begins to deviate from centric potential far away in the strong accumulation region,the exponential form of $ $$-\alpha ={{\phi }_{\text{o}}}-{{\phi }_{\text{s}}}$$ $ in Equation (10) turns out to be negligible. The surface potential in this case can be approximately expressed as

$$\begin{align} \[{{V}_{\text{GS}}}-{{V}_{\text{FB}}}-{{\phi }_{\text{abv}}}=\frac{\sqrt{2q{{\varepsilon }_{\text{si}}}}}{{{C}_{\text{ox}}}}{{\left\{ {{N}_{\text{Tail}}}\exp \frac{\xi ({{T}_{\text{t}}})\cdot {{\phi }_{\text{abv}}}}{{{\phi }_{\text{t}}}} \right\}}^{\frac{1}{2}}}.\] \end{align}$$

(16)

By applying the principle of the Lambert $W$ function^[22],one obtains the surface potential in this region given explicitly by

$$\begin{align} \[{{\phi }_{\text{abv}}}=\left( {{V}_{\text{GS}}}-{{V}_{\text{FB}}} \right)-\frac{2{{\phi }_{\text{t}}}}{\xi ({{T}_{\text{t}}})}{{W}_{0}}\times \sqrt{\frac{{{q}^{2}}{{\varepsilon }_{\text{si}}}{{g}_{\text{t}}}\left( \frac{{{T}_{\text{t}}}}{T} \right)\xi ({{T}_{\text{t}}})\eta ({{T}_{\text{t}}})\exp (\frac{-q({{V}_{\text{ch}}}+{{E}_{\text{Fo}}})}{kT})}{2C_{\text{ox}}^{2}}}\cdot \times \exp \frac{\xi ({{T}_{\text{t}}})({{V}_{\text{GS}}}-{{V}_{\text{FB}}})}{2{{\phi }_{\text{t}}}}.\] \end{align}$$

(17)

Similar to the approach employed in Reference ^[23],Equation (17) is then smoothed with another piece of surface potential to give a unified regional expression. It may be concluded that with a given $

$${{V}_{gs}}$$ $ and $ $${{V}_{ds}}$$ $,both the results of the surface and centric potentials can be obtained by starting from an initial physical-based estimate given by Equation (13). As the gate voltage grows towards the threshold,the electric field vanishes near the middle point of the films as implied by Equation (9) and thus the centric potential tends to be approximately saturated with the maximum value given by Equation (15). The whole process converges quickly to the exact solutions within a few finite steps. Following this,few optimization techniques are needed,which makes the implementation of this scheme more straightforward and suitable for commercial circuit simulators. A more detailed derivation of this approach as well as the related efficiency test can be found in Reference ^[17].

As the accurate values of surface and centric potential have been obtained,by adapting the concept of gradual channel approximation and the Pao-Sah model^[24],the drain current of DG TFT can be expressed as

$$\begin{align} \[{{I}_{\text{ds}}}=2{{\mu }_{\text{eff}}}\frac{W}{L}\int_{0}^{{{V}_{\text{ds}}}}{\int_{{{\phi }_{\text{o}}}}^{{{\phi }_{\text{s}}}}{\frac{{{n}_{\text{free}}}}{F(\phi ,{{V}_{\text{ch}}})}}}\text{d}\phi \text{d}{{V}_{\text{ch}}},\] \end{align}$$

(18)

where $\mu$ _eff is the effective mobility,$W$ is the channel width,$L$ is the effective channel length,and a factor of 2 accounts for the symmetry of the film. Nevertheless,a-Si:H TFTs have unique characteristics of mobility,which strongly depend on the gate voltage as well as the distribution of the DOS. Since a high field exists everywhere in the channel region,the carrier motion in all positive bias regimes is assumed to be the drift current. One may therefore find that it is possible to extend the compact model developed for the case of the sDG MOSFET^[25]. Following this approach,the drain current can be expressed as

$$\begin{align} \[\begin{align} & {{I}_{\text{ds}}}={{\mu }_{\text{fet}}}\frac{W}{L}\left\{ 2{{C}_{\text{ox}}}\left[ \left( {{V}_{\text{gs}}}-{{V}_{\text{fb}}} \right)\left( {{\phi }_{\text{sL}}}-{{\phi }_{\text{so}}} \right)-\frac{1}{2}\left( \phi _{\text{sL}}^{2}-\phi _{\text{so}}^{2} \right) \right] \right. \\ & \left. +4{{\phi }_{\text{t}}}{{C}_{\text{ox}}}\left( {{\phi }_{\text{sL}}}-{{\phi }_{\text{so}}} \right)+\frac{1}{2}{{\varepsilon }_{\text{si}}}{{t}_{\text{si}}}\left( {{\delta }_{\text{L}}}-{{\delta }_{\text{o}}} \right) \right\}, \\ \end{align}$$ \] \end{align}

(19)

where $\phi_{\rm SO} $ and $\phi_{\rm SL} $ are the surface potentials at the source and drain ends,respectively,and the interaction factor $\delta $,which was first proposed for modeling DG MOSFETs in Reference ^[11] is derived as follows. While integrating Equation (7) from the front or back surface to an arbitrary position within the film one obtains

$$\begin{align} \[\begin{align} & {{\text{F}}^{\text{2}}}\left( \phi (\text{x}),{{\text{V}}_{\text{ch}}} \right)\text{-}{{\left[ {{\text{r}}_{\text{G}}}\sum\limits_{\text{i=1}}^{\text{10}}{\left( {{\text{N}}_{\text{i}}}\left\{ \phi \text{+}{{\phi }_{\text{t}}}\ln \left[ \text{1+}{{\text{K}}_{\text{i}}}(\text{-}\frac{\text{q}\phi }{\text{kT}}) \right] \right\} \right)} \right]}^{\text{2}}} \\ & \text{-r}_{\text{t}}^{\text{2}}\exp \frac{\text{q}(\phi \text{-}{{\text{V}}_{\text{ch}}})}{\text{k}{{\text{T}}_{\text{o}}}}\text{-r}_{\text{f}}^{\text{2}}\exp \frac{\text{q}(\phi \text{-}{{\text{V}}_{\text{ch}}})}{\text{kT}}\text{=} \\ & {{\text{F}}^{\text{2}}}\left( {{\phi }_{\text{s/b}}},{{\text{V}}_{\text{ch}}} \right)\text{-}{{\left[ {{\text{r}}_{\text{G}}}\sum\limits_{\text{i=1}}^{\text{10}}{\left( {{\text{N}}_{\text{i}}}\left\{ {{\phi }_{\text{s/b}}}\text{+}{{\phi }_{\text{t}}}\ln \left[ \text{1+}{{\text{K}}_{\text{i}}}(\text{-}\frac{\text{q}{{\phi }_{\text{s/b}}}}{\text{kT}}) \right] \right\} \right)} \right]}^{\text{2}}} \\ & \text{-r}_{\text{t}}^{\text{2}}\exp \frac{\text{q}({{\phi }_{\text{s/b}}}\text{-}{{\text{V}}_{\text{ch}}})}{\text{kT}}\text{-r}_{\text{f}}^{\text{2}}\exp \frac{\text{q}(\phi \text{-}{{\text{V}}_{\text{ch}}})}{\text{kT}}\equiv \gamma \left( {{\phi }_{\text{o}}},{{\text{V}}_{\text{ch}}} \right), \\ \end{align}$$ \] \end{align}

(20)

where $

$${{\phi }_{\text{s}}}$$ $/b is the front or back surface potential,and $ $${{r}_{G}}$$ $ and $ $${{r}_{t}}$$ $ are the parameters related to the density of deep and tail states,respectively^[16]. Since the second expression in Equation (20) depends only on the conditions at the corresponding surfaces,the first expression could therefore be evaluated anywhere and should be equal to a constant which is related to the minimum potential of the film. That constant denoted as $\delta$ could be understood as an interaction factor representing the charge coupling between the front and back gates. For the case of sDG a-Si:H TFTs,$\gamma < 0$ holds at all times which implies that the electric field vanishes near the middle of the film as indicated by Equation (9).

Although Equation (19) seems simple,the complex parts have been incorporated into the calculation of $

$${{\phi }_{\text{ so}}},{{\phi }_{sL}},{{\delta }_{O}},{{\delta }_{L}}$$ $ and the field effect mobility $\mu$ _fet. For n-channel devices,the field effect mobility is defined as low field electron mobility scaled by the ratio of the density of free charge to the total density of the induced charge^[15],i.e.

$$\begin{align} \[{{\mu }_{\text{fet}}}={{\mu }_{\text{o}}}\frac{{{Q}_{\text{free}}}}{{{Q}_{\text{induce}}}},\] \end{align}$$

(21)

where $

$${{\mu }_{\text{o}}}$$ $ is also referred to as band mobility and treated as a material constant in AIM-SPICE^[15]. For the case of MOSFET,$Q_{\rm free} \approx Q_{\rm induced} =2C_{\rm OX} \left( {V_{\rm gs}-V_{\rm t}} \right)$ and therefore,$ $${{\mu }_{\text{fet}}}\approx {{\mu }_{o}}$$ $. However,for DG a-Si:H TFTs,by integrating the free carrier density in the $x$-direction from the interface to the middle of the channel,the total free carrier in DG a-Si:H TFT is written as

$$\begin{align} \[{{Q}_{\text{free}}}=2q\int_{0}^{{{t}_{\text{si}}}/2}{{{N}_{\text{c}}}\exp \frac{q\phi -{{E}_{\text{FO}}}}{kT}}\text{d}x.\] \end{align}$$

(22)

Using the relationship $

$$dx=-\text{d}\phi /F(\phi )$$ $,Equation (22) becomes

$$\begin{align} \[{{Q}_{\text{free}}}=2q\int_{{{\phi }_{\text{o}}}}^{{{\phi }_{\text{s}}}}{\frac{{{N}_{\text{C}}}\exp \frac{q\phi -{{E}_{\text{FO}}}}{kT}}{F\left( \phi ,{{V}_{\text{ch}}} \right)}}\text{d}\phi .\] \end{align}$$

(23)

Therefore,the density of the free carrier in the sub-threshold region,denoted as $

$${{Q}_{\text{fs}}}$$ $,can be approximated by

$$\begin{align} \[{{Q}_{\text{sub}}}\approx {{N}_{\text{C}}}\sqrt{\frac{2\pi {{\varepsilon }_{\text{si}}}kT}{{{N}_{\text{deep}}}}}\exp \frac{q{{\phi }_{\text{s}}}}{kT}\cdot \text{erf}\sqrt{\frac{q\left( {{\phi }_{\text{s}}}-{{\phi }_{\text{o}}} \right)}{kT}},\] \end{align}$$

(24)

where $

$${{N}_{\text{deep}}}=\sum\limits_{i=1}^{10}{{{N}_{\text{i}}}},$$ and erf $\left[\omega \right]$ is the well-known error function. Their polynomial approximations are introduced in Reference ^[26] and their precision is proved to be sufficient for the present compact modeling purpose.

While in the above-threshold region,by following the idea of effective temperature approach given in Reference ^[20],Equation (11) can be transferred to the following form

$$\begin{align} \[{{V}_{\text{g}}}-{{V}_{\text{fb}}}-{{\phi }_{\text{s}}}=\frac{{{\varepsilon }_{\text{si}}}}{{{C}_{\text{ox}}}}\Lambda {{\left[ \left( 1-\exp \frac{q({{\phi }_{\text{o}}}-{{\phi }_{\text{s}}}}{k{{T}_{\text{eff}}}} \right)\times \exp \frac{q{{\phi }_{\text{s}}}}{k{{T}_{\text{eff}}}} \right]}^{\frac{1}{2}}},\] \end{align}$$

(25)

where $

$$\Lambda =\sqrt{2q\left( {{N}_{\text{tail}}}+{{N}_{\text{Fo}}} \right)/{{\varepsilon }_{\text{si}}}}$$ $ and the effective temperature is given by

$$\begin{align} \[{{T}_{\text{eff}}}\left( {{\phi }_{\text{s}}},{{\phi }_{\text{o}}} \right)=\frac{q{{\phi }_{\text{s}}}}{k\ln \frac{F\left( {{\phi }_{\text{s}}},{{\phi }_{\text{o}}} \right)}{\Lambda }}.\] \end{align}$$

(26)

In this case,Equation (23) may be transferred to

$$\begin{align} \[\begin{align} & {{Q}_{\text{fabv}}}=\frac{{{N}_{\text{C}}}}{\Lambda }\frac{1}{\frac{1}{kT}-\frac{1}{k{{T}_{\text{eff}}}\left( {{\phi }_{\text{s}}},{{\phi }_{\text{o}}} \right)}}\times \left( \exp \left\{ q{{\phi }_{\text{s}}}\left[ \frac{1}{kT}-\frac{1}{k{{T}_{\text{eff}}}\left( {{\phi }_{\text{s}}},{{\phi }_{\text{o}}} \right)} \right] \right\} \right. \\ & \left. -\exp \left\{ q{{\phi }_{\text{o}}}\left[ \frac{1}{kT}-\frac{1}{k{{T}_{\text{eff}}}\left( {{\phi }_{\text{s}}},{{\phi }_{\text{o}}} \right)} \right] \right\} \right). \\ \end{align}$$ \] \end{align}

(27)

Note that when the gate voltage $

$${{V}_{gs}}$$ $ becomes large enough,the free charge is largely attributed by the band bending near the a-Si:H/a-Si:H_x:H interface. The carrier motion in this regime is assumed to be the drift current. Since the effect of central potential becomes less significantly as compared with the surface,Equation (27) may further be approximated as

$$\begin{align} \[{{Q}_{\text{fabv}}}=2{{\varepsilon }_{\text{si}}}\frac{{{N}_{\text{c}}}}{q\beta }A{{C}_{\text{ox}}}{{\left( {{V}_{\text{GS}}}-{{V}_{\text{FB}}}-{{\phi }_{\text{s}}} \right)}^{\frac{{{T}_{\text{t}}}}{T}-\frac{1}{2}}},\] \end{align}$$

(28)

where $

$$A={{\left( {{\varepsilon }_{\text{si}}}k{{T}_{\text{t}}}{{N}_{\text{t}}}B \right)}^{-{{T}_{\text{t}}}/T}},B=(\pi T/{{T}_{\text{t}}})/\sin (\pi T/{{T}_{\text{t}}})$$ $ and $\beta =(1/kT)-(1/2kT_{\rm t})$. Equation (28) implies a continuously increasing field effect mobility modulated by gate voltage; A similar phenomenon has also been observed in DG poly-Si TFTs^[8].

Combining Equations (21),(24) and (27) yields the integrated field effect mobility valid for all biases,as is given by

$$\begin{align} \[{{\mu }_{\text{fet}}}={{\left[ \frac{1}{{{\left( 1/{{\mu }_{\text{sub}}} \right)}^{\text{MX}}}+{{\left( 1/{{\mu }_{\text{abv}}} \right)}^{\text{MX}}}} \right]}^{\text{1/MX}}},\] \end{align}$$

(29)

where MX is used to determine the sharpness of transition changing from the weak to strong accumulation regime. Substituting the obtained channel potentials and Equation (29) into Equation (19),one may finally obtain the total drain current in a single-piece formula for describing the $I$-$V$ characteristics of DG a-Si:H TFT. Note that the effect of centric potential has been involved in Equation (26) for definition of the effective temperature,and the assumption that $

$${{n}_{\text{tail}}}\gg {{n}_{free}}$$ $ in deriving Equation (23) is no longer needed.

3. Results and discussion

To verify the proposed scheme,a complete set of solutions of the potentials over the whole region covered by this work is shown in Figure3,where the exact numerical simulation based on Equations (1)-(10) is also presented for comparison. The key parameters used in the analysis are listed in Table1. Note that the key parameters given in $N(E)$ have not been treated as fitting parameters in this work. Instead,they are physical-based and can be experimentally extracted following the approach given in References ^{[27, 28]}. As shown in Figure3,the density of the Gaussian deep state $N$_G has a significant effect on the surface potential in the sub-threshold region. The sub-threshold characteristics of such devices can be improved by reducing both the density of deep states and the channel thickness,which are also easily validated by Equations (12) and (15). The result demonstrated the validity of the scheme and the corresponding approximations.

Figure4 presents the comparison of the proposed solutions of $

$${{\phi }_{\text{s}}}$$ $ with those of single-gate TFTs with analogous DOS distributions. The calculations of the latter are based on the model given in Reference ^[23]. The curve of surface potential as a function of gate voltage rises more sharply in the sub-threshold compared with the latter due to the dual-gate mode. One order of the surface potential derivative with respect to the gate voltage for both cases is shown in the inset. The results clearly show that the proposed scheme is continuous and its accuracy is enough for the prediction of device characteristics. The results of surface potential characteristics under various channel potentials have been given in Figure5. A fairly good agreement with the numerical solution is achieved in both the sub-threshold and strong accumulation regions.

To validate the drain current model based on these potentials,a 2-D symmetrical dual-gate a-Si:H TFT structure has been constructed under MEDICI^[29] by using `MESH' and `TRAP'. The simulation under analysis shares the following common parameters: $L=$ 10 $\mu$m,$t_{\rm si}=$ 80 nm,$t_{\rm oxf}=t_{\rm oxb}=$ 200 nm,N_G}=$ 8 $\times$ 1018 cm-3eV-1,$W_{\rm GA}=$ 0.2 eV,T_t}/T=$ 265/300 K,$g_{\rm t}=$ 3.16 $\times$ 1022 cm^-3e^V-1. The parameters used for the model calculations are: $

$${{\mu }_{\text{o}}}$$ $}=$ 18.8 cm²/(V$\cdot$s),$V_{\rm FB}=$ 0.63 V,$C_{\rm ox}=$ 3.45 $\times$ 10-8 F/cm²,$E_{\rm Fo}=$ 0.64 eV,$N=10$,MX $=$ 1. A low field mobility model has been deployed in the simulation and the short channel effects have not been taken into account for simplicity. Figures 6 and 7 depict the typical transfer characteristics of DG a-Si:H TFT calculated by Equations (19) and (29). The 2-D simulation results have also been given for comparison. One may observe that the current increases sharply by at least five orders of magnitude when the effective gate bias increases from 0 to $+8$ V. This feature is believed to be rather important for the practical application of DG a-Si:H TFT. Both of the figures indicate the validity of the model in predicting the static characteristics of these devices. Since we have modeled the current in different regions separately,the smooth function (29) has been used to combine the separate parts for the current model and is valid in a wide range of operations. Hence,the model may therefore seem to be semi-empirical and less precise in the region between the sub-threshold and the strong accumulation region. Nevertheless,it is a tradeoff between accuracy and complexity. That approach has also been used in References ^{[8, 23]} and proved to be beneficial to shorter computation time in simulation tools.

Figure6 shows that the density of N_G significantly affects the sub-threshold region,where deep states dominate,by shifting this region to positive as the density of N_G increases. In contrast,the effect occurring in the strong accumulation region may be ignored by assuming the same parameters $g_{\rm t and T_t. Figure7 shows the simulation results of $

$${{I}_{ds}}\text{-}{{\text{V}}_{\text{gs}}}$$ $ for various channel thicknesses. As one may see,the curve of the drain current as a function of gate voltage stretches out as the channel thickness increases. This prediction can also easily be confirmed by the observation in the surface potential calculation for different $ $${{t}_{si}}$$ $ as given previously in Figure4 in Reference~^[17].

Another validation is given in Figure8 by comparing this work with the available experimental data from Reference ^[4]. The solid line in Figure8 is the drain current at $

$${{V}_{ds}}=$$ $ 1 and 15V and the dashed curve is the trans-conductance for $ $${{V}_{ds}}=$$ $ 15. It is worth noting that unlike those for DG MOSFETs,the trans-conductance curve of a-Si:H DG TFT does not exhibit a clear peak but continues to increase with gate voltage. This phenomenon implies a consequence of the gate voltage-dependent channel field mobility which is accurately modeled by Equation (28). A fairly good agreement has also been achieved between this work and experimental data from Reference ^[19] in both the linear and saturated region. Since the surface potentials treat the channel pinch-off behavior in a self-consistent way,no threshold and saturation voltages are needed as input parameters for the drain current model. The proposed formulas may be treated as an original point to develop a more advanced model for such DG TFTs; i.e.,as a typical staggered structure device,the phenomenon of current growing is frequently observed near the origin of the output characteristics of these devices. This non-linear contract feature can be easily incorporated by following the approach given in References ^{[16, 23]}.

Other parameters are the same as the ones given in Table1.

4. Conclusion

By considering the combination of Gaussian and exponential distribution of DOS,a physics-based scheme and corresponding approximations have been developed to describe the behavior of the surface potential and potential at the center of the film as a function of applied voltage for DG a-Si:H TFT. The calculations of potentials have been done without the need of solving any transcendental equations. The proposed scheme provides a valuable means for quick evaluation of the behavior of electrostatic potential across the channel thickness. Based on these potentials,a drain current model valid from the sub-threshold to the strong accumulation regime is derived. Only minimum fitting parameters have been involved to ascertain a smooth transition between the different regimes. All of the derived formulas were validated by comparing with the rigorous numerical simulation,and a good agreement has been obtained.